Anwendungsbeispiel: Numerische Integration
Die im vorigen Unterpunkt hergeleiteten numerischen Integrationsregeln werden nun in einem C++ Programm benutzt, um den Wert des bestimmten Integrals einer Funktion $\int_a^b f(x) \, dx$ approximativ zu bestimmen. Die Integrationsregeln lauteten:
Anwendung der Integrationsregeln in einem C++ Programm
In dem folgenden C++ Programm wird das bestimmte Integral der Funktion $f(x)= 10 \, e^{-x/10} \cdot \hbox{sin}(x)$ in den Grenzen [2,4] mittels der numerischen Integrationsregeln approximativ berechnet: $\int_2^4 10 \, e^{-x/10} \cdot \hbox{sin}(x) \, dx$
/* Berechnung des bestimmten Integrals einer Funktion f(x) in den Grenzen [a,b] * mittels unterschiedlicher "closed Newton-Cotes formulars" * (N=1 Trapez-Regel, N=2 Simpson's-Regel, N=3 Simpson's-3/8-Regel und N=4 Regel) */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) double f(double x){ // Definition der Funktion f(x) double wert; wert = 10*sin(x)*exp(-x/10); // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } // Ende der Funktion f(x) double Int_f(double x){ // Definition der analytischen Stammfunktion von f(x) double wert; // (Bem.: benoetigen wir nur zum Vergleich) wert = -100*sin(x)*exp(-x/10)/101 - 1000*cos(x)*exp(-x/10)/101; return wert; } int main(){ // Hauptfunktion double a = 2; // Untergrenze des bestimmten Integrals double b = 4; // Obergrenze des bestimmten Integrals double h; // Deklaration des h-Wertes double I_1, I_2, I_3, I_4; // Deklaration der Integrale der vier Approximationsregel h = (b-a)/1; I_1 = h/2 * (f(a) + f(b)); // N=1 Trapez-Regel h = (b-a)/2; I_2 = h/3 * (f(a) + 4*f(a+h) + f(b)); // N=2 Simpson's-Regel h = (b-a)/3; I_3 = 3*h/8 * (f(a) + 3*f(a+h) + 3*f(a+2*h) + f(b)); // N=3 Simpson's-3/8-Regel h = (b-a)/4; I_4 = 2*h/45 * (7*f(a) + 32*f(a+h) + 12*f(a+2*h) + 32*f(a+3*h) + 7*f(b)); // N=4 Regel // Ausgaben der berechneten Groessen printf("Integral N=1: %14.10f \t Abweichung zum wirklichen Wert: %14.10f \n", I_1, (Int_f(b)-Int_f(a)) - I_1); printf("Integral N=2: %14.10f \t Abweichung zum wirklichen Wert: %14.10f \n", I_2, (Int_f(b)-Int_f(a)) - I_2); printf("Integral N=3: %14.10f \t Abweichung zum wirklichen Wert: %14.10f \n", I_3, (Int_f(b)-Int_f(a)) - I_3); printf("Integral N=4: %14.10f \t Abweichung zum wirklichen Wert: %14.10f \n", I_4, (Int_f(b)-Int_f(a)) - I_4); } // Ende der Hauptfunktion
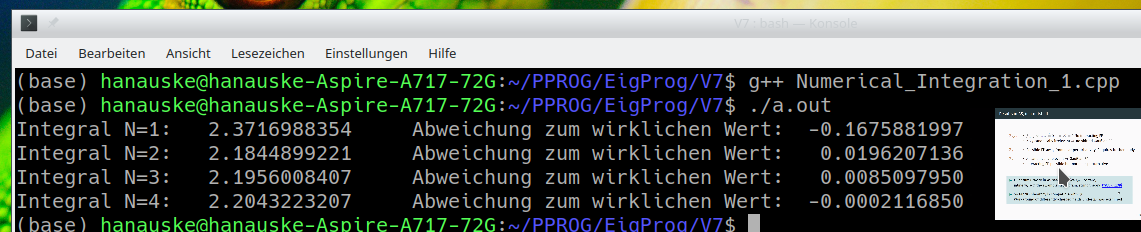
Die nebenstehende Abbildung veranschaulicht die Terminalausgabe des Programms. Man erkennt, dass die berechneten approximativen Resultate dem wirklichen Integralwert desto besser entsprechen, je höher die Ordnung $N$ der Integrationsformel ist.
Stückweise numerische Integration
Da man das betrachtete Integrationsintervall [a,b] ohne einen großen Aufwand in viele Teilintervalle unterglieder kann, ist die stückweise numerische Integration gerade dafür prädestiniert auf dem Computer berechnet zu werden. In dem folgenden C++ Programm wird wieder das bestimmte Integral der Funktion $f(x)= 10 \, e^{-x/10} \cdot \hbox{sin}(x)$ in den Grenzen [2,4] approximativ berechnet, jedoch wird das gesamte Intervall in 'ts' Teilintervalle unterteilt (hier speziell 'ts=3').
/* Berechnung des bestimmten Integrals einer Funktion f(x) in den Grenzen [a,b] * mittels einer stückweise numerischen Integration und * unterschiedlicher "closed Newton-Cotes formulars" * (N=1 Trapez-Regel, N=2 Simpson's-Regel, N=3 Simpson's-3/8-Regel und N=4 Regel) */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) double f(double x){ // Definition der Funktion f(x) double wert; wert = 10*sin(x)*exp(-x/10); // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } // Ende der Funktion f(x) double Int_f(double x){ // Definition der analytischen Stammfunktion von f(x) double wert; // (Bem.: benoetigen wir nur zum Vergleich) wert = -100*sin(x)*exp(-x/10)/101 - 1000*cos(x)*exp(-x/10)/101; return wert; } int main(){ // Hauptfunktion unsigned ts = 3; // Anzahl der Teilintervalle double a = 2; // Untergrenze des bestimmten Integrals double b = 4; // Obergrenze des bestimmten Integrals double h; // Deklaration des h-Wertes double x_u; // x-Untergrenze der Teilintegration double I_1=0, I_2=0, I_3=0, I_4=0; // Deklaration der Integrale der vier Approximationsregel for(unsigned i = 0; i < ts; ++i){ // Schleifen Anfang ueber die einzelnen Teilintegrationen h=(b-a)/(ts*1); // N=1 Trapez-Regel x_u = a + i*h; // Setzen der x-Untergrenze der aktuellen Teilintegration I_1 = I_1 + h/2*(f(x_u) + f(x_u+h)); // N=1 Trapez-Regel h=(b-a)/(ts*2); // N=2 Simpson's-Regel I_2 = I_2 + h/3*(f(x_u) + 4*f(x_u+h) + f(x_u+2*h)); // N=2 Simpson's-Regel h=(b-a)/(ts*3); // N=3 Simpson's-3/8-Regel I_3 = I_3 + 3*h/8*(f(x_u) + 3*f(x_u+h) + 3*f(x_u+2*h) + f(x_u+3*h)); // N=3 Simpson's-3/8-Regel h=(b-a)/(ts*4); // N=4 Regel I_4 = I_4 + 2*h/45*(7*f(x_u) + 32*f(x_u+h) + 12*f(x_u+2*h) + 32*f(x_u+3*h) + 7*f(x_u+4*h)); // N=4 Regel } // Ende for-Schleife // Ausgaben der berechneten Groessen printf("Integral N=1: %14.10f \t Abweichung zum wirklichen Wert: %14.10f \n", I_1, (Int_f(b)-Int_f(a)) - I_1); printf("Integral N=2: %14.10f \t Abweichung zum wirklichen Wert: %14.10f \n", I_2, (Int_f(b)-Int_f(a)) - I_2); printf("Integral N=3: %14.10f \t Abweichung zum wirklichen Wert: %14.10f \n", I_3, (Int_f(b)-Int_f(a)) - I_3); printf("Integral N=4: %14.10f \t Abweichung zum wirklichen Wert: %14.10f \n", I_4, (Int_f(b)-Int_f(a)) - I_4); } // Ende der Hauptfunktion

Die nebenstehende Abbildung veranschaulicht die Terminalausgabe des Programms. Man erkennt wieder, dass die berechneten approximativen Resultate dem wirklichen Integralwert desto besser entsprechen, je höher die Ordnung $N$ der Integrationsformel ist. Vergleicht man die Ergebnisse dieser stückweise numerischen Integration mit den berechneten Werten des vorigen Programms, so erkennt man, das die stückweise numerische Integration genauer ist, unabhängig von der gewählten Integrationsregel.