Anwendungsbeispiel: Nullstellensuche einer Funktion
In diesem Unterpunkt möchten wir ein grundlegendes Problem der numerischen Mathematik behandeln, die Nullstellensuche einer Funktion. Wir betrachten im Speziellen die Funktion $f(x)=e^x-10$ und wollen berechnen, bei welchem x-Wert die Funktion Null wird ($f(x)=0$). Bei der angegebenen Funktion ist das nicht schwierig und man erhält mittels einfacher analytischer Umformungen das Ergebnis $p = $ ln$(10) \approx 2.302585...$ . Eine solche analytische Umformung ist jedoch nicht immer möglich und man kann dann eine Nullstelle auf numerischem Weg mittels unterschiedlicher Methoden berechnen. In diesem Unterpunkt betrachten wir zunächst die Methode der Bisektion (das Intervallhalbierungsverfahren) und danach die Newton-Raphson Methode zur numerischen Ermittlung der Nullstelle.
Der Algorithmus der Bisektion (Intervallhalbierungsverfahren)
Hat eine Funktion im Teilintervall $[a,b] \in ℝ$ eine Nullstelle, so kann man diese Nullstelle numerisch mittels der Methode der Bisektion ermitteln. Betrachten wir z.B. die Funktion $f(x)=e^x-10$ im Teilintervall $[a,b] = [2,4]$. Es gilt $f(2)=e^2-10 \approx -2.61094 < 0$ und $f(4)=e^4-10 \approx 44.59815 > 0$ und somit muss irgendwo zwischen 2 und 4 eine Nullstelle existent sein. Man geht nun wie folgt vor:
Man überprüft ob $f(a) \cdot f(a +\frac{(b-a)}{2})$ größer oder kleiner Null ist. Ist der Wert größer Null, so ist man sicher, dass sich die Nullstelle nicht im Teilintervall $[a,a + \frac{(b-a)}{2}]$ befindet und kann das neue Teilintervall auf $[a + \frac{(b-a)}{2},b]$ setzen. Ist der Wert hingegen kleiner Null, so befindet sich die Nullstelle im Teilintervall $[a, a + \frac{(b-a)}{2}]$, welches man dann als neues Teilintervall verwendet. Der spezielle Fall $f(a) \cdot f(a +\frac{(b-a)}{2}) = 0$ bedeutet, dass die Nullstelle gerade bei $p_0 = p = a +\frac{(b-a)}{2}$ ist und man kann den Algorithmus des Intervallhalbierungsverfahrens abbrechen.
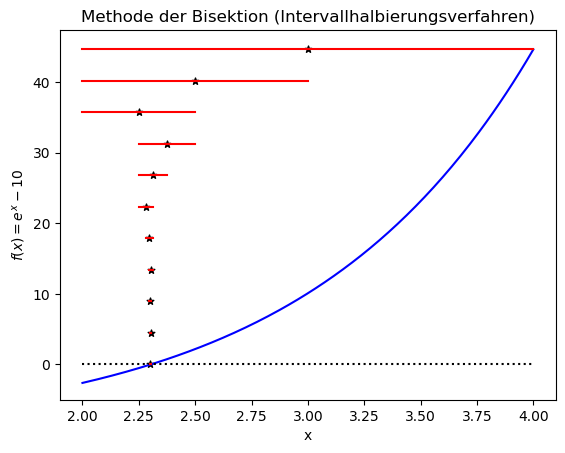
Die nebenstehende Abbildung veranschaulicht die Methode der Bisektion an unserem Beispiel. Die blaue Kurve zeigt die Funktion $f(x)=e^x-10$ im Teilintervall $x \in [2,4]$. Die roten, horizontalen Linien kennzeichnen die jeweiligen Teilintervalle, wobei die oberste Linie das ursprüngliche Teilintervall $[2,4]$ kennzeichnet. Die Mitte des Intervalls ist mit einem schwarzen Stern markiert und dieser Wert stellt auch gleichzeitig den jeweiligen approximierten Wert $p_i$ der Nullstelle dar. Beim Anfangsintervall $[a,b] = [2,4]$ erhält man $p_0 = a +\frac{(b-a)}{2} = 2 +\frac{(4-2)}{2} = 3$ und da $f(a) \cdot f(a +\frac{(b-a)}{2}) = f(2) \cdot f(3) < 0$ ist, befindet sich die wirkliche Nullstelle im Teilintervall $[2,3]$, welches wir bei dann bei der nächsten Iteration als neues Teilintervall $[a,b]$ definieren. Wie wir in der nebenstehenden Abbildung sehen, tastet sich das Intervallhalbierungsverfahren bei fortlaufender Iteration immer näher an den wirklichen Wert der Nullstelle heran.
Das entsprechende C++ Programm des betrachteten Beispiels der Methode der Bisektion (siehe Nullstelle_Bisektion_0.cpp ) ist in dem folgenden Frame abgebildet:
/* Mittels der Methode der Bisektion (Intervallhalbierungsverfahren) * wird die Nullstelle einer Funktion f(x)=0 approximiert * (hier speziell f(x)=exp(x)-10=0) * Ausgabe zum Plotten (Gnuplot oder Python) mittels: "./a.out > Nullstelle_Bisektion_0.dat" */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) double f (double x) { // Deklaration und Definition der Funktion f(x) double wert; // Lokale double-Variable (nur im Bereich der Funktion gültig) wert = exp(x) - 10; // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f(x) } // Ende der Funktion f(x) int main(){ // Hauptfunktion int i; // Deklaration des Laufindex als ganze Zahl double a = 2; // Untergrenze des Intervalls [a,b] in dem f(x)=0 gelten soll double b = 4; // Obergrenze des Intervalls [a,b] in dem f(x)=0 gelten soll const int N = 10; // Anzahl der Iterationen im Intervallhalbierungsverfahren double p, fp; // Deklaration der Variablen des approximierten x- und f(x)-Wertes der Nullstelle double fa=f(a); // Deklaration und Initialisierung des Funktionswertes f(a) an der Untergrenze printf("# 0: Index i der Iteration \n# 1: Approximierter Wert der Nullstelle p_i \n"); // Beschreibung der ausgegebenen Groessen printf("# 2: Funktionswert f(p_i) \n# 3: Relativer Fehler zum wirklichen Wert |(p-p_i)/p| \n"); // Beschreibung der ausgegebenen Groessen printf("# 4: Untergrenze a \n# 5: Obergrenze b \n"); // Beschreibung der ausgegebenen Groessen for(i=0; i<=N; ++i){ // Schleifen Anfang p = a + (b-a)/2; // Festlegung des x-Wertes in der Mitte des Intervalls [a,b] (x=p) fp = f(p); // Berechnung des f(p)-Wertes in der Mitte des Intervalls [a,b] printf("%3d %14.10f %14.10f %14.10f %14.10f %14.10f \n",i, p, fp, fabs((log(10)-p)/log(10)), a, b); // Ausgabe der berechneten Werte if( fa*fp > 0 ){ // Falls der berechnete Wert f(p) das gleiche Vorzeichen hat wie f(a), dann ... a = p; // ... setze die Untergrenze auf a=p und ... fa = fp; // ... lege den neuen Funktionswert an der Untergrenze fest: f(a)=f(p) } else if( fa*fp < 0 ){ // Falls der berechnete Wert f(p) ein unterschiedliches Vorzeichen hat wie f(a), dann ... b = p; // ... setze die Obergrenze auf b=p } else{ // Falls durch der berechnete Funktionswert gerade Null ist (f(p)=0 -> f(a)*f(p)=0), dann ... i = N; // ... beende das Bisektion-Verfahren vorzeitig } // else Ende } // Ende der for-Schleife des Bisektion-Verfahres }
Das C++ Programm verwendet eine Funktionendefinition (siehe Unterpunkt Funktionen in C++) und benutzt die, im Unterkapitel C++ Anweisungen: Auswahlanweisungen mit if und switch dargestellte (if-else)-Anweisung. Hierbei wäre es vielleicht sinnvoller gewesen, wenn anstatt der geschachtelten (if-else)-Anweisung eine switch-Anweisung verwendet worden wäre.
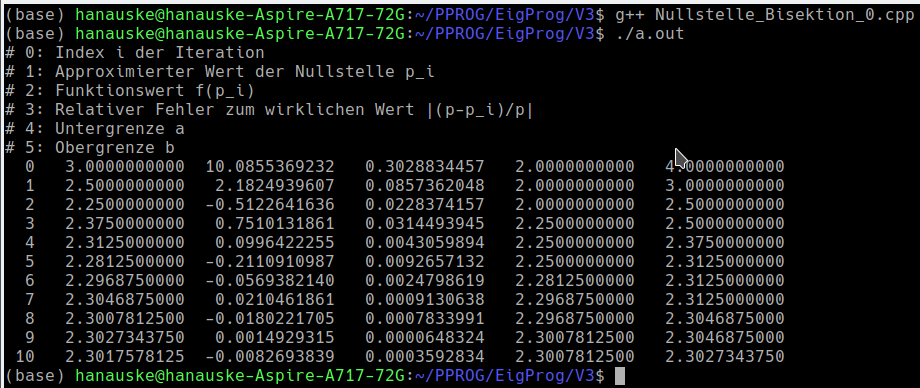
Zunächst wird die Funktion $f(x)=e^x-10$ außerhalb der main()-Funktion definiert, wobei für den Namen der Funktion einfach 'f', als Argumentenliste nur eine double Variable und als Rückgabetyp ebenfalls double verwendet wurde. Am Anfang der main()-Funktion werden zunächst mehrere Variablen definiert, wobei z.B. die Integer Variable 'N' als eine konstante ganze Zahl deklariert und mit dem Wert '10' initialisiert wurde. Diese Variable spezifiziert die Anzahl der Iterationen im Intervallhalbierungsverfahren. Das Programm gibt in jedem Durchlauf sechs unterschiedliche Werte aus, deren Beschreibung dann zunächst im Terminal ausgegeben wird. Neben dem approximierten Wert der Nullstelle $p_i$, und dem relativen Fehler zum wirklichen Wert ($\left| \frac{\hbox{ln}(10) - p_i}{\hbox{ln}(10)} \right|$) werden auch die jeweiligen Unter- und Obergrenzen des betrachteten Teilintervalls ausgegeben (siehe nebenstehende Terminalausgabe). Der eigentliche Algorithmus des Intervallhalbierungsverfahrens ist mittels einer for-Schleifenanweisung und einer geschachtelten (if-else)-Anweisung realisiert worden. Für den sehr unwarscheinlichen Fall, dass $f(a) \cdot f(a +\frac{(b-a)}{2}) = 0$ ist, wird der Index 'i' der Iteration auf den Wert 'N' gesetzt und das Programm verlässt die for-Schleife, da die Nullstelle exakt ermittelt wurde. Man erkennt schon an den berechneten Zahlenwerten der Terminalausgabe, dass der relative Fehler zum wirklichen Wert in jedem Iterationsschritt kleiner wird und auch der Unterschied zwischen der Ober- und Untergrenze des betrachteten Teilintervalls immer kleiner wird.
Die Visualisierung der im Terminal ausgegebenen Ergebnisse kann man mit dem folgenden Python Skript realisieren, wobei zuvor die ausgegebenen Daten wieder mit dem Trick './a.out > PythonPlot_Bisektion_0.dat' in eine Datei 'PythonPlot_Bisektion_0.dat' umgeleitet wurden.
# Python Programm zum Plotten der berechneten Daten von (Nullstelle_Bisektion_0.cpp) import matplotlib.pyplot as plt # Python Bibliothek zum Plotten (siehe https://matplotlib.org/ ) import numpy as np # Python Bibliothek fuer Mathematisches (siehe https://numpy.org/ ) data = np.genfromtxt("./Nullstelle_Bisektion_0.dat") # Einlesen der berechneten Daten von Nullstelle_Bisektion_0.cpp plt.title(r'Methode der Bisektion (Intervallhalbierungsverfahren)') # Titel der Abbildung plt.ylabel(r'$f(x)=e^x - 10$') # Beschriftung y-Achse plt.xlabel('x') # Beschriftung x-Achse x_interval=np.linspace(data[0,4], data[0,5], 200) # x-Intervall [a,b] als Liste von 200 Zahlen plt.plot(x_interval,np.exp(x_interval)-10, color="blue") # Plotten der Funktion f(x) im Intervall [a,b] plt.plot([data[0,4],data[0,5]],[0,0], color="black", linestyle=":") # Plotten einer horizontale Null-Linie y=0 y_interval=np.linspace(np.exp(x_interval[-1])-10, 0, int(data[-1,0])+1) # y-Bereich zum Veranschaulichen der unterschiedlichen Intervalle for i in data[:,0]: # Schleife um die einzelnen Resultate der Nullstelle Bisektion zu plotten index=int(i) # Umwandlung des Laufindex in eine Integer Zahl plt.plot([data[index,4],data[index,5]],[y_interval[index],y_interval[index]], color="red") # Plotten des i-ten Intervalls plt.scatter(data[index,1],y_interval[index], marker='*', color="black", s=25) # Plotten des i-ten p-Wertes plt.savefig("Nullstelle_Bisektion_0.png", bbox_inches="tight") # Speichern der Abbildung als Bild plt.show() # Zusaetzliches Darstellen der Abbildung in einem separaten Fenster
Im Python-Skript PythonPlot_Bisektion_0.py werden zunächst die berechneten Daten eingelesen und der Titel und die Achsenbeschriftungen gemacht. Die danach folgenden drei Zeilen plotten die Funktion $f(x)$ im Bereich $[2,4]$ als blaue Kurve. Um die jeweiligen Teilintervalle als diskrete horizontale Linien darstellen zu können, definieren wir die Liste 'y_interval', welche gerade 'N+1' äquidistante Werte im Bereich $[0,f(4)]$ beinhaltet. Die einzelnen Resultate der Bisektionsiteration werden schließlich mittels einer Python for-Schleife realisiert und die einzelnen Teilintervalle als horizontale rote Linien und der approximierte Nullstellenwert $p_i$ als Stern mittels der Funktion 'plt.scatter(...)' geplottet. Man erhält so das Bild, welches am Anfang dieses Unterkapitels als Illustration des Intervallhalbierungsverfahrens benutzt wurde.
Die Newton-Raphson Methode
Die Newton-Raphson Methode der Nullstellenermittlung ist ein sehr effektives Verfahren zur Ermittlung einer Nullstelle. Im Gegensatz zur Methode der Bisektion hat dieses Verfahren jedoch den Nachteil, dass man neben der Funktion $f(x)$ zusätzlich auch noch die erste Ableitung der Funktion ($f^\prime(x) = \frac{df(x)}{dx}$) im Teilintervall $[a,b]$ benötigt. Die Newton-Raphson Methode basiert auf dem Prinzip der Taylorreihenentwicklung der Funktion, wobei man nur die ersten beiden Terme der Reihenentwicklung berücksichtigt und alle nicht-linearen Terme vernachlässigt. Man nimmt hierbei an, dass die Funktion im Teilintervall $[a,b]$ eine Nullstelle bei $x=p \in [a,b]$ hat ($f(p)=0$) und rät im 0-ten Schritt des Algorithmus einen x-Wert, der nahe dieser Nullstelle liegen soll. Wir bezeichnen diesen geratenen Wert im Folgenden mit $p_0$ und entwickeln unsere Funktion um diesen Wert in eine Taylorreihe $$ \begin{equation} f(x) = f(p_0) + \left( x - p_0 \right) \cdot f^\prime(p_0) + \frac{\left( x - p_0 \right)^2}{2} \cdot f^{\prime\prime}(p_0) \, + \, ... \quad . \end{equation} $$ Betrachtetet man nun die taylorentwickelte Funktion bei $x=p$ und nimmt an, dass der Wert von $p_0$ nahe der wirklichen Nullstelle ist, so erhält man: $$ \begin{eqnarray} &0 = f(p) = f(p_0) + \left( p - p_0 \right) \cdot f^\prime(p_0) \, \underbrace{+ \, \frac{\left( p - p_0 \right)^2}{2} \cdot f^{\prime\prime}(p_0) \, + \, ...}_{\approx \, 0} \,\,\, \approx \,\, f(p_0) + \left( p - p_0 \right) \cdot f^\prime(p_0) &\\ & \Longrightarrow p \approx p_0 - \frac{f(p_0)}{f^\prime(p_0)} & \end{eqnarray} $$ In der Newton-Raphson Methode benutzt man nun diesen neu approximierten Wert der Nullstelle und nimmt diesen für eine neue Iteration. Der Algorithmus benutzt somit die folgende Gleichung um die n-te Approximation der Nullstelle $p_n$ mithilfe der (n-1)-ten Approximation zu berechnen: $$ \begin{equation} p_n = p_{n-1} - \frac{f(p_{n-1})}{f^\prime(p_{n-1})} \, , \quad \hbox{mit:} \,\, n \geq 1 \end{equation} $$
Das entsprechende C++ Programm des betrachteten Beispiels der Newton-Raphson Methode (siehe Nullstelle_NewtonRaphson_1.cpp ) ist in dem folgenden Frame abgebildet:
/* Mittels der Newton-Raphson Methode * wird die Nullstelle einer Funktion f(x)=0 approximiert * (hier speziell f(x)=exp(x)-10 = 0) * Ausgabe zum Plotten (Gnuplot oder Python) mittels: "./a.out > Nullstelle_NewtonRaphson_1.dat" */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) int main(){ // Hauptfunktion int i; // Deklaration des Laufindex als ganze Zahl double p=2; // Deklaration des approximierten x-Wertes der Nullstelle und Start-Initialisierung const int N=10; // Anzahl der Iterationen in der Newton-Raphson Methode double fp, fp_s; // Deklaration der Variablen des approximierten f(x)-Wertes der Nullstelle und dessen Ableitung f'(x) printf("# 0: Index i der Iteration i \n# 1: Approximierter Wert der Nullstelle p_i \n"); // Beschreibung der ausgegebenen Groessen printf("# 2: Funktionswert f(p_i) \n# 3: Relativer Fehler zum wirklichen Wert |(p-p_i)/p| \n"); // Beschreibung der ausgegebenen Groessen printf("# 4: Ableitung von f: f'(p_i) \n"); // Beschreibung der ausgegebenen Groessen for(i=0; i<=N; ++i){ // For-Schleife der Newton-Raphson Methode fp=exp(p)-10; // Berechnung des f(p)-Wertes fp_s=exp(p); // Berechnung der Ableitung (f'(p)-Wert) printf("%3d %20.14f %20.14f %20.14f %20.14f \n",i, p, fp, fabs((log(10)-p)/log(10)), fp_s); // Ausgabe der berechneten Werte p = p - fp/fp_s; // Berechnung des neuen p-Wertes mittels der Newton-Raphson Methode } // Ende der For-Schleife der Newton-Raphson Methode }
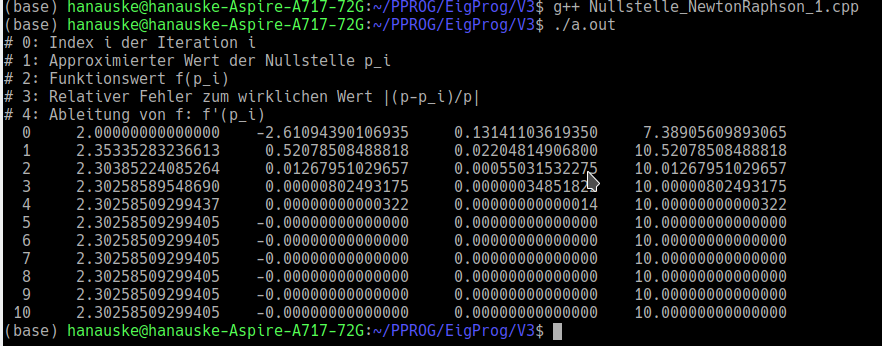
Das C++ Programm ist möglichst kurz konstruiert und es wurden z.B. auch keine Funktionendefinitionen für die Funktionen $f(x)$ und $f^\prime(x)$ verwendet. Am Anfang der main()-Funktion werden wieder zunächst mehrere Variablen definiert, wobei z.B. die Integer Variable 'N' als eine konstante ganze Zahl deklariert und mit dem Wert '10' initialisiert wurde und der initiale Anfangswert der Nullstelle auf $p_0=2$ gesetzt wurde. Neben dem approximierten Wert der Nullstelle $p_i$, und dem relativen Fehler zum wirklichen Wert ($\left| \frac{\hbox{ln}(10) - p_i}{\hbox{ln}(10)} \right|$) wird z.B. auch der Wert der Ableitung der Funktion $f^\prime(p_i)$ ausgegeben (siehe nebenstehende Terminalausgabe). Der eigentliche Algorithmus der Newton-Raphson Methode ist wieder mittels einer for-Schleifenanweisung realisiert worden, wobei hier keine C++ Auswahlanweisung bei der Implementierung benötigt wurde. Man erkennt an den berechneten Zahlenwerten der Terminalausgabe, dass der relative Fehler zum wirklichen Wert in jedem Iterationsschritt kleiner wird und sich ab der fünften Iteration nicht mehr ändert, da der approximierte Wert der Nullstelle innerhalb der Genauigkeit der benutzten double-Variablen dem wirklichen Wert $p$ entspricht. Die Newton-Raphson Methode ist somit ein sehr effektives Verfahren zur Ermittlung einer Nullstelle.
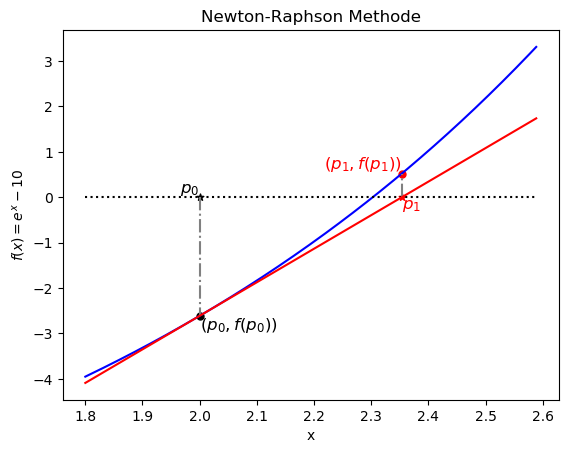
Das nebenstehende Bild wurde mittels des Python Skriptes PythonPlot_NewtonRaphson_1.py erzeugt und es veranschaulicht den ersten Iterationsschritt der Newton-Raphson Methode grafisch. Der mittels des Startwertes bei $x=p_0=2$ berechnete neue Wert der approximierten Nullstelle $p_1$ ergibt sich, indem man die Tangentengleichung am Punkt $(p_0,f(p_0))$ berechnet (siehe rote Gerade) und den Schnittpunkt dieser Geraden mit der x-Achse bestimmt.