Anwendungsbeispiel: Folgen und Reihen
In diesem Unterpunkt sollen einige Anwendungsbeispiele der for-, while- und do-Schleifen (siehe C++ Anweisungen: Die for-, while- und do-Schleifen) diskutiert werden. Es werden im Speziellen zunächst die konvergente Folge der Eulersche Zahl $e$ und die Leibniz-Reihe zur Berechnung der Kreiszahl $\pi$ vorgestellt. Obwohl es bei der numerischen Berechnung von Folgen und Reihen besser ist, eine for-Schleife zu verwenden (offensichtliche Schleifenvariable, Aktualisierung der Schleifenvariable am Ende des 'Anweisungsblockes'), wird in diesen Anwendungsbeispielen stets eine while-Schleife verwendet. Das Umschreiben der Programme unter Verwendung einer for-Schleife ist den Studierenden überlassen (siehe Übungsblatt Nr. 3 , Aufgabe 2). Am Ende dieses Unterpunktes wird die logistische Abbildung behandelt, welche ebenfalls ein interessantes Anwendungsbeispiel einer diskreten Folge darstellt und als ein Paradebeispiel einer diskreten Gleichung im Zusammenhang mit chaotischem Verhalten angesehen wird (siehe z.B. Walter Greiner, 'Klassische Mechanik II' [8. Auflage, 2008, Kapitel 27. Seite 478]).
Anwendung: Mathematische Folgen
Im Übungsblatt Nr. 2 in der Aufgabe 1 wurde bereits die Folge $(a_n)_{n \in ℕ}$ mit $a_n := \left( 1 + \frac{1}{n} \right)^n$ vorgestellt, die als Grenzwert die Eulersche Zahl $e$ hat: \[ \begin{equation} e = \lim \limits_{n \to \infty} \left( 1 + \frac{1}{n} \right)^n \end{equation} \] Wir sind nun zunächst nicht an dem genauen Wert dieses Grenzwertes interessiert, sondern möchten das Konvergenzverhalten der Folge $a_n$ studieren und uns die ersten $N$ Folgenglieder mittels eines C++ Programms ausgeben lassen. Das folgende Programm gibt z.B. die ersten 20 ($N=20$) Folgenglieder auf 15 Nachkommastellen genau aus
/* Die Eulerschen Zahl e wird mittels ihrer Folgendefinition approximiert * Ausgabe zum Plotten (Gnuplot oder Python) mittels: "./a.out > While_4.dat" */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) int main(){ // Hauptfunktion unsigned int n = 1; // Deklaration und Initialisierung des Folgenindex als naturliche Zahl const unsigned int N=20; // Deklaration und Initialisierung des maximalen Folgengliedes double e_Approx; // Deklaration der approximierten Gleitkommazahl von e printf("# 0: Folgenindex n \n# 1: Approximierter Wert von e \n"); // Beschreibung der ausgegebenen Groessen while( n <= N ){ // Schleife zur Berechnung von e mit Abbruchbedingung e_Approx = pow(1 + 1.0/n,n); // Mathematische Folgendefinition fuer die Eulerschen Zahl e printf("%3i %20.15f \n",n, e_Approx); // Ausgabe des approximierten Wertes von e n++; // Index der Folge wird um eins erhöht (entspricht n=n+1) } // Ende der Schleife }
, wobei die nebenstehende Abbildung die erzeugte Terminalausgabe zeigt. Anhand der ausgegebenen Werte erkennt man schon gut das Konvergenzverhalten der Folge, jedoch wäre es doch schöner, die Daten in einem Diagramm sich darzustellen. Es gibt nun mehrere Möglichkeiten, sich die von einem C++ Programm berechneten Simulationsdaten zu visualisieren. Im Folgenden werden zwei unterschiedliche Varianten vorgestellt: Die Darstellung mittels Gnuplot (siehe Gnuplot Homepage und Installation von Gnuplot unter Linux) und Python (siehe Matplotlib: Visualization with Python), wobei wir im weiteren Verlauf der Vorlesung ausschließlich die Python-Variante verwenden werden. Für beide Varianten ist es jedoch zunächst nötig, die im Terminal ausgegebenen Daten in einer separaten Datei zu speichern (z.B. in der Datei 'While_4.dat'). Man könnte die Ausgabe zwar auch direkt vom C++ Programm in eine Datei schreiben (dies behandeln wir in einer späteren Vorlesung). Im Folgenden werden wir jedoch die Datenumleitung in eine externe Datei mit einem Linux-Trick machen, den wir schon in Vorlesung 1 (siehe Programmiersprachen) kennengelernt hatten. Hierbei gibt man die Eingabezeile './a.out > While_4.dat' im Linux-Terminal ein und leitet dadurch die Terminalausgabe in die Datei 'While_4.dat' um.

Für die Visualisierung der Daten mittels Gnuplot habe ich Ihnen schon ein fertiges Gnuplot-Shellskript zum Download bereitgestellt (siehe Gnuplot-Shellskript: GnuPlot_While_4.sh). Bitte laden Sie sich dieses Skript herunter, platzieren es in dem gleichen Ordner, in welchem sich die erzeugte Datei 'While_4.dat' befindet und ändern die Rechte der heruntergeladenen Skriptdatei, sodass es ausführbar wird (Eingabe von 'chmod +rwx GnuPlot_While_4.sh' im Terminal). Startet man nun das Gnuplot-Skript mittels './GnuPlot_While_4.sh', so erscheint die rechts oben abgebildete Ausgabe im Terminal und zusätzlich wird eine Bilddatei (GnuPlot_While_4.png) erzeugt, die unsere Daten visualisiert (siehe Abbildung unten links). Das entsprechende Gnuplot-Shellskript ist unten rechts abgebildet.
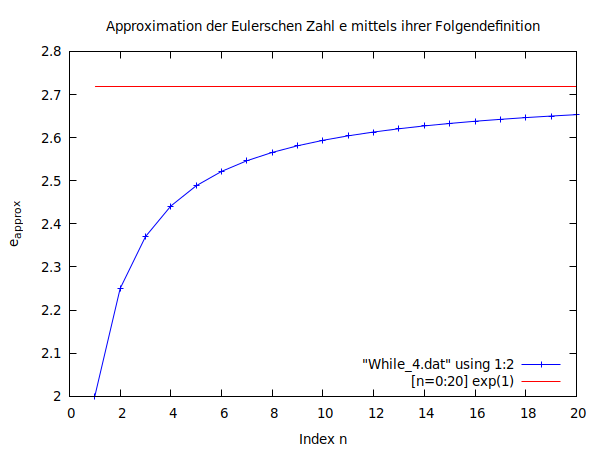
# Shell Script zum Plotten der berechneten Daten von (While_4.cpp) mittels Gnuplot FILE=While_4.dat echo "Starte Plotten mit Gnuplot" gnuplot -persist << PLOT reset set terminal pngcairo size 600,450 enhanced font 'Verdana,10' ################################################ set title "Approximation der Eulerschen Zahl e mittels ihrer Folgendefinition" set ylabel "e_{approx}" set xlabel "Index n" set key right bottom set output sprintf('GnuPlot_While_4.png') plot "$FILE" using 1:2 with linespoints lt rgb "blue", [n=0:20] exp(1) with lines lt rgb "red" ################################################ quit PLOT echo "Fertig"
Im abgebildeten Gnuplot-Shellskript wird zunächst die Datei definiert, in der sich die zu plottenden Daten befinden ( FILE=While_4.dat ) und danach wird die eine Terminalausgabe mittels echo "Starte Plotten mit Gnuplot" gemacht. Es sei hier noch erwähnt, dass sowohl in Gnuplot als auch in Python, die Zeilen welche mit dem Rautesymbol '#' beginnen ignoriert werden und somit wie Komentarzeilen fungieren. Diese Eigenschaft wurde bei der 'Beschreibung der ausgegebenen Größen' im C++ Programm verwendet (printf("# 0: Folgenindex n \n# 1: Approximierter Wert von e \n");). Das Plot-Programm 'Gnuplot' startet man im Terminal mit dem Befehl 'gnuplot'. Es werden dann mit den Befehlen 'set ...' mehrere Plot-Eigenschaften spezifiziert (z.B. der Titel des Diagramms: set title "...", die Bezeichnung der x- und y-Achsen, die Position der Plotlegende: set key, oder der Dateiname des zu erstellenden Diagramms). Das eigentliche Plotten der Daten wird mit dem Befehl 'plot "$FILE" using 1:2 ...' bewerkstelligt. Zusätzlich zu den Daten wird noch eine horizontale rote Linie in das Diagramm eingefügt, die den Referenzwert der Zahl $e$ veranschaulicht (mittels '..., [n=0:20] exp(1) ...').
Gnuplot ist ein mächtiges Programm für die Visualisierung von Daten, auf das wir aber an dieser Stelle nicht weiter eingehen werden. Der interessierte Leser findet unter dem folgenden Link weiteres Material: Gnuplot Homepage
Im Folgenden werden wir die in die Datei 'While_4.dat' geschriebenen Daten mittels Python visualisieren. Hierfür habe ich Ihnen ebenfalls ein fertiges Python-Skript zum Download bereitgestellt (siehe Python-Skript: PythonPlot_While_4.py). Bitte laden Sie sich dieses Skript herunter und platzieren es in dem gleichen Ordner in welchem sich die erzeugte Datei 'While_4.dat' befindet. Im Gegensatz zum Gnuplot-Shellskript müssen Sie bei dem Python-Skript die Rechte der heruntergeladenen Datei nicht ändern, sodass es ausführbar wird. Startet das Python-Skript mittels des Terminalbefehls 'python3 PythonPlot_While_4.py', so wird die Bilddatei 'PythonPlot_While_4.png' erzeugt (siehe Abbildung unten links) und zusätzlich erscheint ein neues, interaktives Fenster mit dem x-y-Diagramm (siehe Abbildung unten rechts).
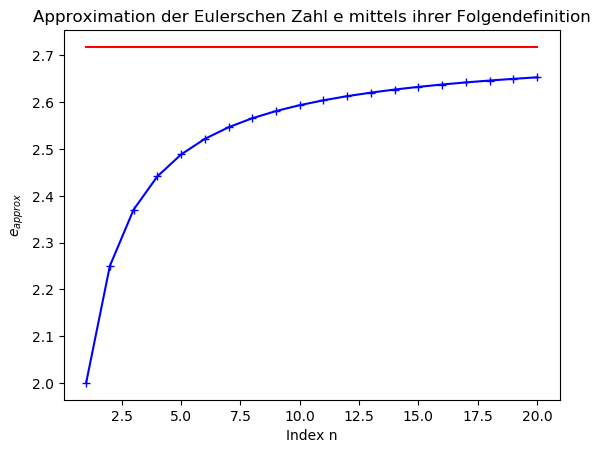
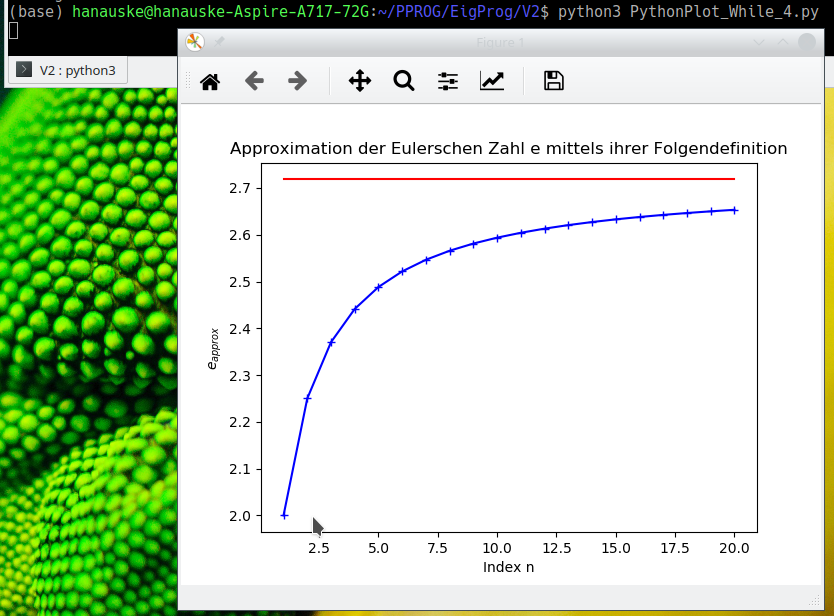
In dem interaktiven Diagrammfenster kann der Benutzer z.B., indem er zuvor auf das Symbol mit der Lupe klickt, gewisse Teilbereiche der Abbildung vergrößert darstellen. Um die Linux-Shell wieder benutzen zu können, muss man zuvor das interaktive Fenster schließen. In der unteren Abbildung ist das entsprechende Python-Skript dargestellt. Dieses wird in dem nächsten Unterpunkt der Vorlesung besprochen (siehe Eine kleine Einführung in die Programmiersprache Python).
# Python Programm zum Plotten der berechneten Daten von (While_4.cpp) import matplotlib.pyplot as plt # Python Bibliothek zum Plotten (siehe https://matplotlib.org/ ) import numpy as np # Python Bibliothek fuer Mathematisches (siehe https://numpy.org/ ) data = np.genfromtxt("./While_4.dat") # Einlesen der berechneten Daten von While_4.cpp plt.title(r'Approximation der Eulerschen Zahl e mittels ihrer Folgendefinition') # Titel der Abbildung plt.ylabel(r'$e_{approx}$') # Beschriftung y-Achse plt.xlabel('Index n') # Beschriftung x-Achse plt.plot(data[:,0],data[:,1], marker='+', color="blue") # Plotten der Daten plt.plot([data[0,0],data[-1,0]],[np.e,np.e], color="red") # Horizontale Linie, die den exakten Wert von e markiert plt.savefig("PythonPlot_While_4.png", bbox_inches="tight") # Speichern der Abbildung als Bild plt.show() # Zusaetzliches Darstellen der Abbildung in einem separaten Fenster
Anwendung: Mathematische Reihen
Wir betrachten im Folgenden das mathematische Problem der Berechnung der Kreiszahl $\pi = 3.141592653589793...$ und verwenden dafür die im Jahre 1682 von Gottfried Wilhelm Leibniz vorgestellte iterative Annäherung. Die sogenannte alternierende Leibniz-Reihe konvergiert im Limes $\lim \limits_{N \to \infty}$ zu dem Wert der irrationalen Zahl $\frac{\pi}{4}$: \[ \begin{equation} \sum_{k=0}^N \frac{(-1)^k}{2 k +1} = 1 - \frac{1}{3} + \frac{1}{5} \, - ... + \frac{(-1)^N}{2 N +1} ,\quad \hbox{mit:} \quad \sum_{k=0}^\infty \frac{(-1)^k}{2 k +1} = \frac{\pi}{4} \end{equation} \] Das folgende C++ Programm gibt die ersten 100 ($N=100$) Folgenglieder der Partialsumme der Leibniz-Reihe auf 15 Nachkommastellen genau aus und vergleicht am Ende den so approximierten Wert von $\pi$ mit seinem Wirklichen:
/* Mittels der Leibniz-Reihe * (Gottfried Wilhelm Leibniz, Zeitschrift Acta Eruditorum, 1682) * wird die Kreiszahl Pi approximiert * (Anzahl der Summanden = N) * Ausgabe zum Plotten (Gnuplot oder Python) mittels: "./a.out >> While_2.dat" */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) int main(){ // Hauptfunktion unsigned int k = 0; // Definition des Summenindex als ganze Zahl const unsigned int N = 100; // Definition der Anzahl der mitgenommenen Summenglieder als konstante ganze Zahl double Pi_Approx = 0; // Definition der approximierten Gleitkommazahl von Pi (Datentyp 'double') printf("# 0: Summenindex k \n# 1: Approximierter Wert von Pi \n"); // Beschreibung der ausgegebenen Groessen while( k <= N ){ // Schleife zur Berechnung von Pi/4 mit Abbruchbedingung Pi_Approx = Pi_Approx + pow(-1,k)/(2*k + 1); // Innerer Teil der Leibniz-Reihe printf("%4i %20.15f \n",k, 4*Pi_Approx); // Ausgabe des approximierten Wertes von Pi ++k; // Index der Summe wird um eins erhöht } // Ende der Schleife Pi_Approx = Pi_Approx*4; // Leibniz-Reihe liefert Pi/4, deshalb hier mal 4 printf("# Approximierter Wert von Pi: %20.15f \n", Pi_Approx); // Ausgabe des approximierten Wertes printf("# Wirklicher Wert von Pi: %20.15f \n", M_PI); // Ausgabe des wirklichen Wertes }
Der approximierte Zahlenwert von $\pi$ ($\pi_{approx}$) wird am Anfang des Programms als double-Variable deklariert und auf den Wert Null initialisiert (double Pi_Approx = 0;). Im Gegensatz zum Programm While_4.cpp der Folgenberechnung der Zahl $e$, muss man hier den approximierten Wert in einer Variable speichern (im Programm While_4.cpp hätte man die einzelnen Folgenglieder auch direkt mittels des printf(...)-Befehls ausgeben lassen können, ohne eine extra Variable deklarieren zu müssen). Beim ersten Durchlauf der while-Schleife besitzt der Summenindex 'k' und die Variable 'Pi_Approx' somit den Wert Null. Durch die Anweisung 'Pi_Approx = Pi_Approx + pow(-1,k)/(2*k + 1);' wird der Variable 'Pi_Approx' ein neuer Wert zugewiesen, der sich aus einer Addition seines alten Wertes (Pi_Approx=0) mit dem Zahlenwert $\frac{(-1)^0}{2 \cdot 0 +1}=1$ ergibt. Nach dieser Anweisung besitzt die Variable somit den Wert Eins (Pi_Approx = 1). In der darauf folgenden printf(...)-Ausgabe wird der aktuelle Wert von $k$ ($k=0$) und der aktuelle Wert von vier mal 'Pi_Approx' ausgegeben. Eine Multiplikation mit vier wird hierbei deshalb gemacht, da die unendliche Leibniz-Reihe ja $\frac{\pi}{4}$ liefert. Nach der Ausgabe wird der Summenindex $k$ um Eins erhöht und die Anweisungsbedingung der while-Schleife ( k <= N ) testet, ob ein erneutes Durchlaufen der Schleife nötig ist. Da ja nun '1 = k <= N = 100' gilt, sind noch viele weitere Durchläufe nötig, bis schließlich '101 = k <= N = 100' eine falsche Aussage ist und die Schleife beendet wird. Beim zweiten Durchlauf der Schleife ist zunächst $k=1$ und 'Pi_Approx=1' und ein erneutes Berechnen der Anweisung 'Pi_Approx = Pi_Approx + pow(-1,k)/(2*k + 1);' liefert 'Pi_Approx'$=1+\frac{(-1)^1}{2 \cdot 1 +1}=1+\frac{-1}{3}=\frac{2}{3}$, sodass in der Terminalausgabe der Wert $4 \cdot \frac{2}{3} \approx 2.666666666666667$ erscheint. Die folgenden beiden Abbildungen zeigen das Konvergenzverhalten der Leibniz-Reihe (siehe linke untere Abbildung) und die letzten Werte der Terminalausgabe des C++ Programms (siehe rechte untere Abbildung).
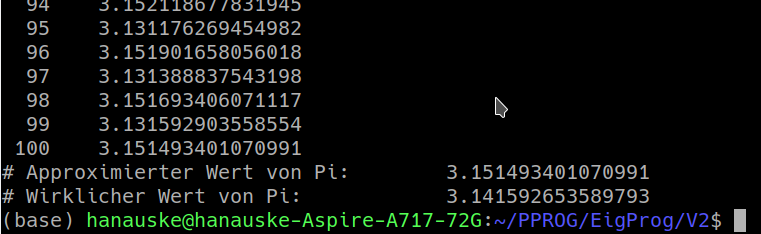
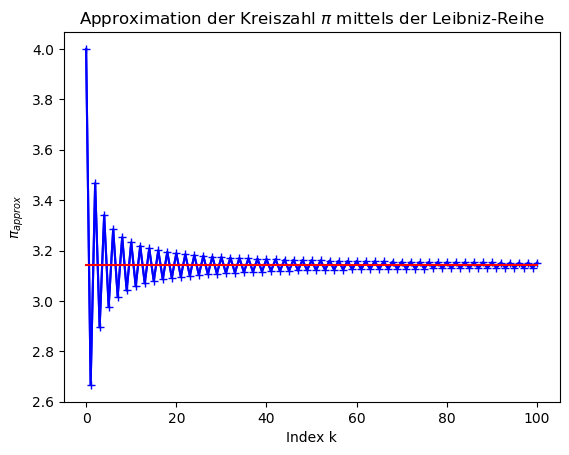
Die Terminalausgabe der while-Schleife endet bei $k=100$ und die letzten beiden Zeilen stellen die beiden printf(...)-Befehle dar, die sich außerhalb der while-Schleife befinden. Es wird hier der letzte approximierte Zahlenwert von $\pi$ ($\pi_{approx}= 4 \cdot$ 'Pi_Approx') mit dem wirklichen Wert von $\pi$ verglichen, wobei der "wirkliche Wert" durch die in <cmath> vordefinierte double Zahl 'M_PI' gegeben ist. Man erkennt hierbei, dass der mit $N=100$ erhaltene approximierte Wert von $\pi$ lediglich auf drei Nachkommastellen genau ist. Dies liegt unter anderem an dem alternierenden Verhalten der Leibniz-Reihe, welches man gut in der linken Abbildung erkennt. Die Abbildung stellt die Zahlenwerte der printf(...)-Befehle des inneren Teils der while-Schleife dar und wurde mithilfe des unten abgebildeten Python-Skripts erzeugt, wobei zuvor die ausgegebenen Daten wieder mit dem Trick './a.out > While_2.dat' in eine Datei 'While_2.dat' umgeleitet wurden. Das Python-Skript: PythonPlot_While_2.py ist dem Skript Python-Skript: PythonPlot_While_4.py von seiner Struktur her sehr ähnlich und es wurden lediglich die eingelesene Datei, der Titel, die Beschreibungen der x- und y-Achsen, die Position der roten horizontalen Linie und der Name der zu speichernden Bilddatei verändert.
# Python Programm zum Plotten der berechneten Daten von (While_2.cpp) import matplotlib.pyplot as plt # Python Bibliothek zum Plotten (siehe https://matplotlib.org/ ) import numpy as np # Python Bibliothek fuer Mathematisches (siehe https://numpy.org/ ) data = np.genfromtxt("./While_2.dat") # Einlesen der berechneten Daten von While_2.cpp plt.title(r'Approximation der Kreiszahl $\pi$ mittels der Leibniz-Reihe') # Titel der Abbildung plt.ylabel(r'$\pi_{approx}$') # Beschriftung y-Achse plt.xlabel('Index k') # Beschriftung x-Achse plt.plot(data[:,0],data[:,1], marker='+', color="blue") # Plotten der Daten plt.plot([data[0,0],data[-1,0]],[np.pi,np.pi], color="red") # Horizontale Linie, die den exakten Wert von Pi markiert plt.savefig("PythonPlot_While_2.png", bbox_inches="tight") # Speichern der Abbildung als Bild plt.show() # Zusaetzliches Darstellen der Abbildung in einem separaten Fenster
Die logistische Abbildung
Die logistische Abbildung stellt ein einfaches demographisches Modell dar, welches die zeitliche evolutionäre Entwicklung einer Population (z.B. eine Population von Heuschrecken) in einem begrenzten Lebensraum mathematische versucht zu beschreiben. Hierbei berücksichtigt das Modell der logistischen Abbildung, dass sich die Population einerseits durch Fortpflanzung vermehrt, als auch andererseits durch Überbevölkerung ihre Reproduktionsrate sinken kann. Das mathematische Modell besitzt die folgende Gestalt \[ \begin{equation} x_{n+1} \,=\, a \cdot x_n \left( 1 - x_n \right) \quad \forall \,\, x_n \in [0,1] \, , \,\, n \in ℕ \quad \hbox{und} \quad a \in (1,4] \quad , \end{equation} \] wobei $x_n$ die Populationsdichte (Anzahl der Individuen relativ zu einer theoretischen Maximalgröße) zu einem diskreten Zeitpunkt $n$ ist und die Größe des sogenannten Bifurkationsparameters (Verzweigungsparameter) $a$ durch die Fortpflanzungs- und Sterberaten bestimmt wird. Unter der Voraussetzung $ a > 1 $ und $x_{n} << 1$ ist die Vermehrungsrate ($x_{n+1} - x_{n}$) positiv, nähert man sich jedoch der Sättigungsdichte $x = 1$, dann sinkt durch Überbevölkerung (volle Ausschöpfung des Lebensraumes und entsprechender Nahrungsmangel) die Reproduktionsrate, sodass $x_{n+1} < x_{n}$ ist ($x_{n+1} - x_{n}$ ist negativ).
Das folgende C++ Programm gibt z.B. die ersten 50 ($N=50$) Folgenglieder der logistischen Abbildung mit $a=2.8$ auf 15 Nachkommastellen genau aus.
/* Logistische Abbildung * Ausgabe zum Plotten (Gnuplot oder Python) mittels: "./a.out > Logi.dat" */ #include <iostream> // Ein- und Ausgabebibliothek int main(){ // Hauptfunktion const unsigned int N = 50; // Definition der Anzahl der Folgenglieder als konstante ganze Zahl double a = 2.8; // Verzweigungsparameter (Bifurkationsparameter) als double Zahl a in (1,4] double x = 0.1; // Wert der Folge als double Zahl (Populationsdichte), Anfangswert x_0 in [0,1] printf("# 0: Folgenindex n \n# 1: Wert der Folge x_n \n"); // Beschreibung der ausgegebenen Groessen for(int n=0; n<=N; ++n){ // for-Schleife ueber die Folgenwerte printf("%4i %20.15f \n",n, x); // Ausgabe des Folgenindex und Folgenwertes x = a*x*(1 - x); // Math. Modell der logistischen Abbildung } // Ende der Schleife } // Ende Hauptfunktion
Obwohl der mathematische Ausdruck der logistischen Abbildung und das entsprechende Programm relativ einfach aussieht, sind die Resultate der Simulationen äußerst komplex und vielschichtig. Liegt der Bifurkationsparameter im Bereich $1 < a < 3$, so strebt die Folge $x_n$ gegen einen stabilen Fixpunkt ($\lim \limits_{n \to \infty} x_n = 1-1/a$), was bedeutet, dass nach langer Zeit die Population einen evolutionär stabilen Endzustand erreicht. Für Werte $3 \leq a < 3.57$ findet man hingegen periodische Lösungen, d.h. die Folge $x_n$ pendelt zwischen zwei oder mehreren Werten hin und her. Im Bereich $3.57 \leq a < 4$ verhält sich schließlich die Folge chaotisch und man spricht hierbei von einem deterministischen Chaos. Die unteren Abbildungen zeigen einige der möglichen Simulationsergebnisse des C++ Programms und wurden mit dem Python-Skript: PythonPlot_Logi.py angefertigt.
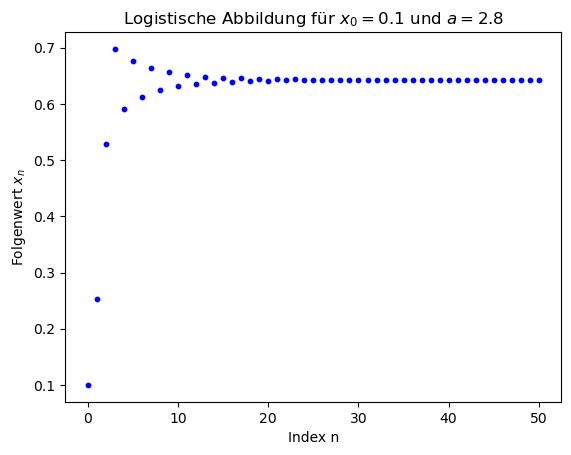

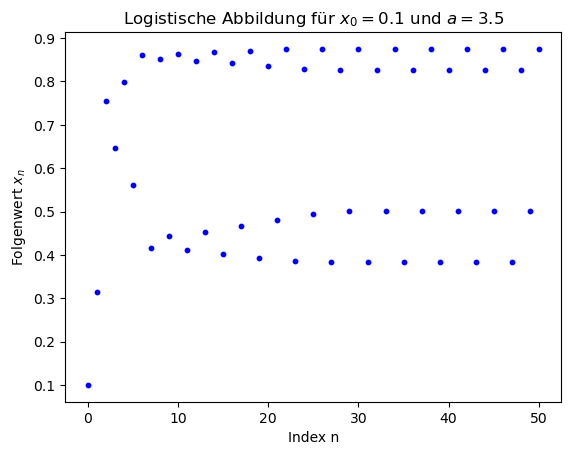
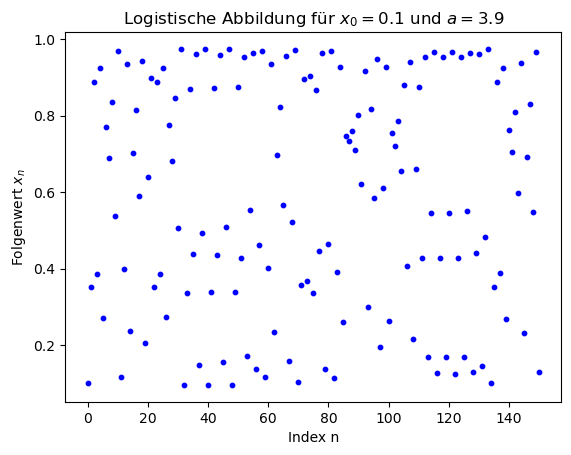
In allen vier Simulationen hat der erste Folgenwert den Betrag $x_0=0.1$, d.h. die Population ist am Anfang noch recht klein (nur 10% ihrer Maximalgröße). Im linken Bild ($a=2.8$) nähert sich die Population asymptotisch dem evolutionär stabilen Endzustand $\lim \limits_{n \to \infty} x_n = 1-1/a \approx 0.64286$ an. In den beiden mittleren Diagrammen finden wir periodische Lösungen. Bei $a=3.3$ pendelt die Population nach einiger Zeit zwischen zwei Werten $0.47943, 0.82360$ und bei $a=3.5$ zwischen vier Werten $0.38282, 0.82694, 0.50088, 0.87500$ hin und her. Im rechten oberen Bild ($a=3.9$) sehen wir hingegen ein chaotisches Verhalten der Population, das auch nach 150 Folgenwerten keine geordnete periodische Struktur zeigt. Die Population kann z.B. plötzlich fast ihre Maximalgröße erreichen ($x_n \approx 0.9737$) und im nächsten Zeitschritt dann auf einen Wert von $x_{n+1} \approx 0.0999$ fallen. Zusätzlich schaukeln sich minimale Veränderungen des Anfangswertes $x_0$ nach einiger Zeit so auf, dass eine Vorhersage der Populationsentwicklung in diesem chaotischen Bereich praktisch nicht machbar ist.
Die logistische Gleichung ist die wohl meist betrachtete diskrete Gleichung im Zusammenhang mit chaotischem Verhalten. Um eine systematische Analyse der logistischen Abbildung und einen globalen Überblick über das Verhalten dieses teils-chaotischen Systems zu erhalten, erstellt man gewöhnlich ein Attraktordiagramm (Feigenbaum-Diagramm). Die Abfolge von regulären und chaotischen Bereichen werden hierbei visualisiert, indem man die Folgenwerte als Funktion eines Systemparameters (hier der Bifurkationsparameter $a$) darstellt. Im klassischen Feigenbaum-Diagramm lässt man bei den regulären Lösungen eine gewisse Anzahl der ersten Werte weg und stellt nur die Folgenwerte dar, die sich nach einiger Zeit als Attraktoren herauskristallisieren.
Das folgende C++ Programm kombiniert eine while-Schleife mit einer for-Schleife, um für mehrere Werte des Bifurkationsparameters $a$ die Folgenwerte der logistischen Abbildung auszugeben.
/* Attraktordiagramm der logistischen Abbildung (Feigenbaum-Diagramm) * Ausgabe zum Plotten (Gnuplot oder Python) mittels: "./a.out > Logi_AttrDiag.dat" */ #include <iostream> // Ein- und Ausgabebibliothek int main(){ // Hauptfunktion const unsigned int N = 300; // Definition der Anzahl der Folgenglieder als konstante ganze Zahl double a = 2.8; // Verzweigungsparameter (Bifurkationsparameter) als double Zahl a in (1,4] double x; // Wert der Folge als double Zahl printf("# 0: Verzweigungsparameter a \n# 1...: Werte der Folge x_n \n"); // Beschreibung der ausgegebenen Groessen while( a < 4 ){ // while-Schleife ueber die Werte des Verzweigungsparameter printf("%8.4f ", a); // Ausgabe des Verzweigungsparameter x = 0.1; // Initialisierung Anfangswert x_0 in [0,1] for(int n=0; n<=N; ++n){ // for-Schleife ueber die Folgenwerte printf("%20.15f ", x); // Ausgabe des Folgenwertes x = a*x*(1 - x); // Math. Modell der logistischen Abbildung } // Ende der for-Schleife a = a + 0.0025; // Erhoehung des Verzweigungsparameter um 0.0025 printf("\n"); // Ausgabe neue Zeile } // Ende while-Schleife } // Ende Hauptfunktion
In dem Programm werden für jeden der 481 unterschiedlichen $a$-Werte 300 Folgenwerte ausgegeben. Die untere Abbildung auf der rechten Seite zeigt das Attraktordiagramm der logistischen Abbildung (klassisches Feigenbaum-Diagramm), wobei die ersten 100 Folgenwerte nicht dargestellt sind (siehe Python-Skript: PythonPlot_Logi_AttrDiag.py). Die untere Abbildung auf der linken Seite zeigt hingegen das Attraktordiagramm der logistischen Abbildung für alle Folgenwerte, wobei die zeitliche Entwicklung des Folgenwertes durch eine unterschiedliche Farbwahl visualisiert wurde (siehe Python-Skript: PythonPlot_Logi_AttrDiag_a.py).
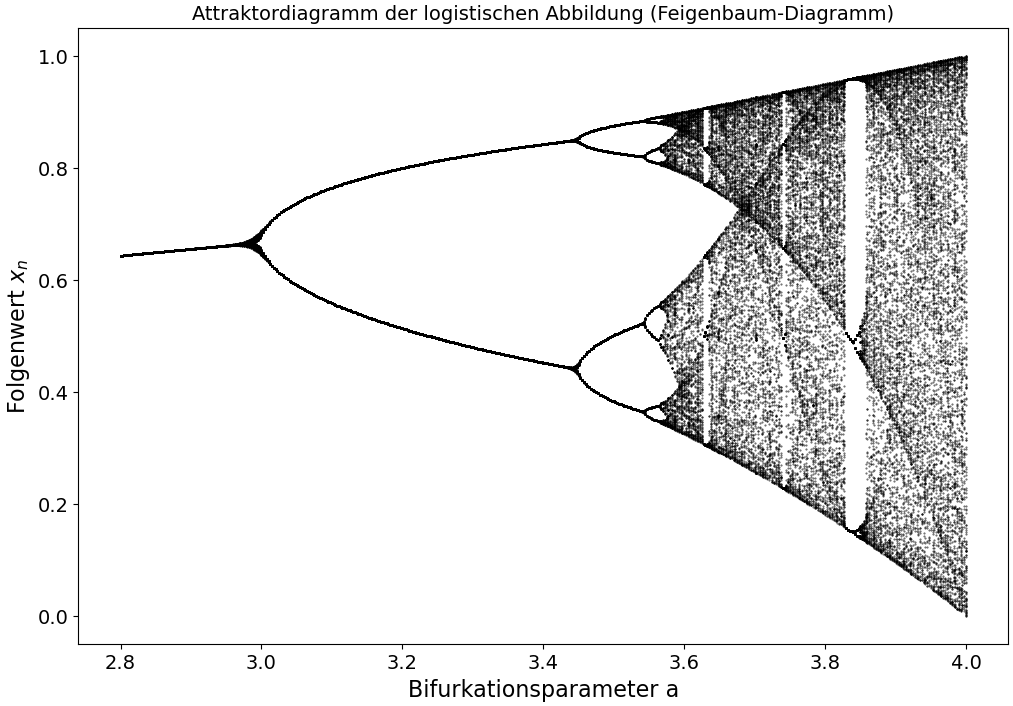
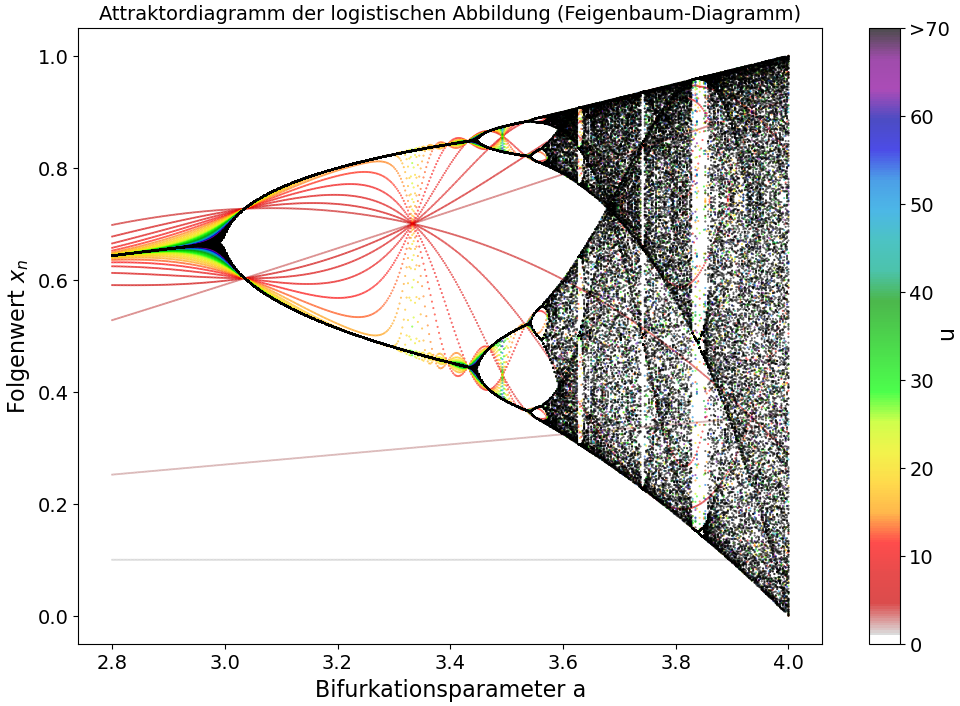
In den oberen Feigenbaum-Diagrammen sind die sogenannten Heugabel-Bifurkation (Heugabel-Verzweigungen), bei denen stets eine Periodenverdopplung der periodischen Lösung auftritt, gut zu erkennen. Die Abbildungen zeigen auch, dass der Weg in das Chaos über eine Kaskade von mehreren Heugabel-Bifurkation führt.
In den folgenden Unterpunkten dieser Vorlesung möchte ich nochmals auf die Die Computerarithmetik und auf den Fehler in numerischen Berechnungen vertiefend eingehen und Ihnen dann noch eine kleine Einführung in die Programmiersprache Python geben.