Das Doppelpendel
Das Doppelpendel ist ein Anwendungsfall aus der klassischen Mechanik (siehe Walter Greiner, 'Klassische Mechanik II' [8. Auflage, 2008, Kapitel V15. Seite 269]). Das System besteht aus zwei miteinander verbundenen Pendeln, wobei wir die Luftreibung zunächst vernachlässigen. Die Herleitung der Bewegungsgleichungen des Doppelpendels erfolgt am elegantesten mittels der Euler-Lagrange Gleichungen, bzw. mittels der Hamilton Theorie. In der Euler-Lagrange Theorie beschreibt man das Doppelpendel mittels zweier generalisierten Koordinaten $\theta_1(t)$ und $\theta_2(t)$, welche die Ausschläge der beiden Pendel als Pendelwinkel zur Vertikalen beschreiben. Die generalisierten Geschwindigkeiten $\dot{\theta_1}(t)$ und $\dot{\theta_2}(t)$ stellen die Winkelgeschwindigkeiten der beiden Pendel dar. Die Lagrangefunktion ergibt sich, indem man die potentielle Energie $V$ des Systems von seiner kinetischen Energie $T$ subtrahiert ($L = T - V$). Die potentielle Energie definieren wir dabei relativ zu einer Ebene im Abstand $l_1 + l_2$ unterhalb des Aufhängepunktes des Doppelpendels. Betrachtet man die Bewegung des Doppelpendels in der x-y-Ebene, so ergibt sich die folgende Lagrangefunktion des Systems $$ \begin{eqnarray} L = T - V &=& \frac{1}{2} m_1 \left[ \dot{x_1}(t)^2 + \dot{y_1}(t)^2 \right] + \frac{1}{2} m_2 \left[ \dot{x_2}(t)^2 + \dot{y_2}(t)^2 \right] - V \\ \hbox{mit:} && x_1 = l_1 \, \hbox{sin}(\theta_1) \, , \,\, y_1 = - l_1 \, \hbox{cos}(\theta_1) \quad , \,\, x_2 = l_1 \, \hbox{sin}(\theta_1) + l_2 \, \hbox{sin}(\theta_2) \, , \,\, y_2 = - l_1 \, \hbox{cos}(\theta_1) - l_2 \, \hbox{cos}(\theta_2) \\ && V = V(\theta_1,\theta_2) = m_1 \, g \left[ l_1 - l_1 \, \hbox{cos}(\theta_1) \right] + m_2 \, g \left[ l_1 + l_2 - \left( l_1 \, \hbox{cos}(\theta_1) + l_2 \, \hbox{cos}(\theta_2) \right) \right] \quad , \end{eqnarray} $$ wobei $m_1$ und $m_2$ die Massen und $l_1$ und $l_2$ die Längen der beiden Pendel darstellen.
Mittels der Lagrange-Gleichungen $$ \begin{equation} \frac{d }{dt} \left( \frac{\partial L}{\partial \dot{\theta}_1} \right) - \frac{\partial L}{\partial \theta_1} \, =\, 0 \quad \hbox{und} \quad \frac{d }{dt} \left( \frac{\partial L}{\partial \dot{\theta}_2} \right) - \frac{\partial L}{\partial \theta_2} \, =\, 0 \end{equation} $$ gelangt man zu zwei gekoppelten Differentialgleichungen zweiter Ordnung, die man dann in ein System von vier gekoppelten DGLs erster Ordung umschreiben muss um sie numerisch lösen zu können.
Von den Euler-Lagrange Gleichungen zur Bewegungsgleichung mittels SymPy
In dem Jupyter Notebook Das Doppelpendel berechnen wir zunächst die Bewegungsgleichungen des Doppelpendels auf analytischem Weg, indem wir unter Verwendung der SymPy Bibliothek die Euler-Lagrange Gleichungen des Doppelpendels bestimmen. Danach schreiben wir die Bewegungsgleichung in ein System von erster Ordnung Differentialgleichungen um.
Numerische Lösung mit C++ und Python
Wir werden die numerische Lösung der Differentialgleichung sowohl mit Python, als auch mit einem C++ Programm erstellen. In beiden Fällen müssen wir jedoch zunächst das System von zwei gekoppelten Differentialgleichungen zweiter Ordnung in ein System von vier Differentialgleichungen erster Ordnung überführen. Näheres zum numerischen Lösen von Differentialgleichungen finden Sie in der Vorlesung Einführung in die Programmierung für Studierende der Physik (Sommersemester 2025), speziell in Vorlesung 9 Systeme von gekoppelten Differentialgleichungen und Differentialgleichungen zweiter Ordnung und in dem Jupyter Notebook Systeme von gekoppelten Differentialgleichungen und Differentialgleichungen zweiter Ordnung.
Umschreiben der Bewegungsgleichung in ein System von Differentialgleichungen erster Ordnung
Wir schreiben nun das System von Bewegungsgleichung zweiter Ordnung in ein System von vier miteinander gekoppelten Differentialgleichungen erster Ordnung um. Wir betrachten nun die numerische Lösung und machen die folgenden Variablenumbenennung: $u_1(t)=\theta_1(t)$, $u_2(t)=\theta_2(t)$, $u_3(t)=\dot{\theta}_1(t)$, $u_4(t)=\dot{\theta}_2(t)$ und definieren das System von DGLs wie folgt: $$ \begin{eqnarray} \dot{u_1}(t) &=& \frac{d u_1}{dt} = \frac{d \theta_1}{dt} = u_3(t) \\ \dot{u_2}(t) &=& \frac{d u_2}{dt} = \frac{d \theta_2}{dt} = u_4(t) \\ \dot{u_3}(t) &=& \frac{d u_3}{dt} = \frac{d \dot{\theta_1}}{dt} = \ddot{\theta}_1(t) := f_1(u_1,u_2,u_3,u_4)\\ \dot{u_4}(t) &=& \frac{d u_4}{dt} = \frac{d \dot{\theta_2}}{dt} = \ddot{\theta}_2(t) := f_2(u_1,u_2,u_3,u_4) \end{eqnarray} $$ Die Funktionen $f_1(u_1,u_2,u_3,u_4)$ und $f_2(u_1,u_2,u_3,u_4)$ sind dabei die mittels der Euler-Lagrange Gleichungen berechneten analytischen sympy-Gleichungen (siehe Jupyter Notebook Das Doppelpendel). Die sympy-Ausdrücke der Bewegungsgleichungen, die Funktionen $f_1(u_1,u_2,u_3,u_4)$ und $f_2(u_1,u_2,u_3,u_4)$, können auch vom Notebook in C++-Ausdrücke umgewandelt werden und dann im C++-Programm implementiert werden.
In dem Jupyter Notebook Das Doppelpendel (Doppelpendel.ipynb) benutzen wir zum Lösen des gekoppelten Systems von Differentialgleichungen das Python-Modul SciPy, welches eine breite Kollektion von mathematischen Algorithmen und Funktionen bereitstellt. Im Speziellen werden wir die Funktion 'solve_ivp(...)' verwenden, die sich im Untermodul 'scipy.integrate' befindet, welches Funktionen zum Lösen von gewöhnlichen Differentialgleichungen bereitstellt.
Das C++ Programm
Wir möchten nun das obere System von vier gekoppelten Differentialgleichungen erster Ordnung mit einem C++ Programm numerisch Lösen. Dazu verwenden wir als Vorlage das im Projekt Die schwingende Kette erstellte Programm SchwingendeKette.cpp. In diesem objektorientierten C++ Programm hatten wir den Kern-Algorithmus der numerischen Lösung (Runge-Kutta Ordnung vier Verfahren) in einer C++ Klasse auslagern. Die Klasse 'dsolve' war dabei so allgemein gehalten, das sie die Berechnung der numerischen Lösung für eine beliebige Anzahl von gekoppelten Differentialgleichungen erster Ordnung generieren konnte. In dem folgenden Programm (Doppelpendel.cpp) verwenden wir nun diese Klasse zum Simulieren der Bewegung des periodisch angetriebenen Pendels.
// Das Doppelpendel /* Beispiel eines schwingenden Systems aus dem Bereich der Mechanik * welches bei gewissen Parameterkonstellationen deterministisch chaotische Bewegungen zeigt * Berechnung der Loesung eines Systems von Differentialgleichungen * mittels Runge-Kutta Ordnung vier Verfahren * Verfahren zur Loesung der DGL ist in einer Klasse ausgelagert * Zeitentwicklung, t-Werte in [a,b] * Konstruktor: dsolve(Anfangszeit a, Endzeit b, Anzahl der Punkte N, Anfangswerte alpha=y(a), DGL als Funktion, Laenge Pendel1, Laenge Pendel2) * Ausgabe zum Plotten mittels Python Jupyter Notebook Doppelpendel.ipynb: "./a.out > Doppelpendel.dat" */ #include <iostream> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <vector> // Vector-Container der Standardbibliothek #include <functional> // Funktionen in der Argumentenliste von Funktionen using namespace std; // Benutze den Namensraum std // Klasse zum Loesen der DGL des Doppelpendels class dsolve{ //Definition der Klasse 'dsolve' double a = 0; // Untergrenze des Zeit-Intervalls [a,b] in dem die Loesung berechnet werden soll double b = 1; // Obergrenze des Intervalls [a,b] int N = 10; // Anzahl der Punkte in die das t-Intervall aufgeteilt wird vector<double> alpha = {0,0,0,0}; // Vier Anfangswerte (Ort und Geschwindigkeit der beiden Pendel) bei t=a vector<vector<double>> y_RungeK_4; // Deklaration eine double Vektor-Matrix zum speichern der Loesungen vector<double> Zeit; // Deklaration eines double Vektors zum speichern der Zeit-Werte public: // Konstruktor mit sieben Argumenten (Initialisierung der Parameter, Uebergabe der DGL als Funktion, Berechnung der Loesung der DGL) dsolve(double a_, double b_, unsigned int N_, vector<double> alpha_, function< vector<double>(double, vector<double>, double, double)> f, double l1, double l2) : a(a_),b(b_),N(N_),alpha(alpha_) { double h = (b - a)/N; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) int n = alpha_.size(); // Anzahl der Anfangswerte bzw. DGL-Gleichungen vector<double> k1(n),k2(n),k3(n),k4(n); // Deklaration der vier Runge-Kutta Parameter fuer jede Loesung vector<double> y(n); // Temporaerer Hilfsvektor Zeit.push_back(a_); // Zum Zeit-Vektor die Anfangszeit eintragen y_RungeK_4.push_back(alpha_); // Zum Loesungs-Vektor die Anfangswerte eintragen for(int i=0; i < N; ++i){ // for-Schleife ueber die einzelnen Punkte des t-Intervalls for(int j=0; j < n; ++j){k1[j] = h*f(Zeit[i],y_RungeK_4[i],l1,l2)[j];} // for-Schleife ueber die vier Runge-Kutta k1-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + k1[j]/2;} // Temporaerer Hilfsvektor for(int j=0; j < n; ++j){k2[j] = h*f(Zeit[i]+h/2,y,l1,l2)[j];} // for-Schleife ueber die vier Runge-Kutta k2-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + k2[j]/2;} // Temporaerer Hilfsvektor for(int j=0; j < n; ++j){k3[j] = h*f(Zeit[i]+h/2,y,l1,l2)[j];} // for-Schleife ueber die vier Runge-Kutta k3-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + k3[j];} // Temporaerer Hilfsvektor for(int j=0; j < n; ++j){k4[j] = h*f(Zeit[i]+h,y,l1,l2)[j];} // for-Schleife ueber die vier Runge-Kutta k4-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + (k1[j] + 2*k2[j] + 2*k3[j] + k4[j])/6;} // Temporaerer Hilfsvektor y_RungeK_4.push_back(y); // Zum Loesungs-Vektor den neuen Wert eintragen Zeit.push_back(a + (i+1)*h); // Zum Zeit-Vektor die neue Zeit eintragen } // Ende for-Schleife ueber die einzelnen Punkte des t-Intervalls }; // Ende des Konstruktors const vector<vector<double>>& get_y() const { return y_RungeK_4; } // Definition der konstanten Member-Funktion get_y(), Rueckgabewert Vektor-Matrix der Loesung der DGL const vector<double>& get_zeit() const { return Zeit; } // Definition der konstanten Member-Funktion get_zeit(), Rueckgabewert vector der zeit-Punkte }; // Ende der Klasse // Definition der Bewegungsgleichung des Doppelpendels vector<double> dgls(double t, vector<double> u_vec, double l1, double l2){ // Laenge Pendel1 l1, Laenge Pendel2 l2 double g {9.81}; // Erdbeschleunigung double m1 {1.0}; // Masse Pendel 1 double m2 {1.0}; // Masse Pendel 2 vector<double> du_dt; du_dt.push_back(u_vec[2]); // Vier DGLs erster Ordnung du_dt.push_back(u_vec[3]); // eigentliche Bewegungsgleichung folgt du_dt.push_back((g*m1*sin(u_vec[0]) + g*m2*sin(u_vec[0])/2 + g*m2*sin(u_vec[0] - 2*u_vec[1])/2 + l1*m2*pow(u_vec[2],2)*sin(2*u_vec[0] - 2*u_vec[1])/2 + l2*m2*pow(u_vec[3],2)*sin(u_vec[0] - u_vec[1]))/(l1*(-m1 + m2*pow(cos(u_vec[0] - u_vec[1]),2) - m2))); du_dt.push_back((-g*m1*sin(u_vec[1]) + g*m1*sin(2*u_vec[0] - u_vec[1]) - g*m2*sin(u_vec[1]) + g*m2*sin(2*u_vec[0] - u_vec[1]) + 2*l1*m1*pow(u_vec[2],2)*sin(u_vec[0] - u_vec[1]) + 2*l1*m2*pow(u_vec[2],2)*sin(u_vec[0] - u_vec[1]) + l2*m2*pow(u_vec[3],2)*sin(2*u_vec[0] - 2*u_vec[1]))/(2*l2*(m1 - m2*pow(cos(u_vec[0] - u_vec[1]),2) + m2))); return du_dt; // Rueckgabewert der DGLs als Standard-Vektor } // Ende: Definition der Bewegungsgleichung-Funktion // Hauptfunktion int main(){ dsolve Loes {0,50,10000,{M_PI/4.0,sqrt(2)*M_PI/4.0,0,0},dgls,1,1}; // Benutzt Konstruktor mit a=0, b=50, N=10000, l1=1, l2=2 printf("# 0: Index i \n# 1: t-Wert \n# 2: theta_1 \n# 3: theta_2 \n# 4: d_theta_1 \n# 5: d_theta_2 \n"); // Beschreibung der ausgegebenen Groessen for(int i=0; i < Loes.get_zeit().size(); ++i){ // for-Schleife zur Terminalausgabe; Zeitwerte printf("%3d %19.15f %19.15f %19.15f %19.15f %19.15f \n",i, Loes.get_zeit()[i], Loes.get_y()[i][0], Loes.get_y()[i][1], Loes.get_y()[i][2], Loes.get_y()[i][3]); // Ausgabe Index, Zeitwert und vier Pendelwerte } // Ende der for-Schleife } // Ende der Hauptfunktion
In dem oben abgebildeten C++ Programm ist die numerische Lösung der Differentialgleichung innerhalb einer Klassenstruktur implementiert, wobei als Klassenname 'dsolve' verwendet wurde. Das zugrundeliegende, zu lösende Differentialgleichungssystem ist in einer vektorwertigen Funktion 'vector<double> dgls(double t, vector<double> u_vec, double l1, double l2){' definiert, die an den Konstruktor der Klasse als Argument übergeben wird. Hier unterscheidet sich das die Klasse dsolve ein wenig von ihrer Vorlage SchwingendeKette.cpp. Da in der Argumentenliste der 'dgls'-Funktion zusätzlich auch die Parameter der Längen der Pendel 'l1' und 'l2' aufgelistet werden, wurde die Struktur der Funktion 'f' im Konstruktor der Klasse leicht abgeändert und zusätzlich die Parameter 'l1' und 'l2' auch der Argumentenliste des Konstruktors zugefügt. Diese Erweiterung wurde gemacht, damit der Benutzer im Hauptprogramm in einfacher Weise die Parameter der Pendellängen verändern kann. Die Bewegungsgleichung des Doppelpendels ist nicht-linear und, abhängig von den Anfangsbedingungen können sehr unterschiedliche und teilweise chaotische Bewegungsformen auftreten.
Numerische Ergebnisse
Im Folgenden werden wir nur einen kleinen Ausschnitt aus dem Parameterraum des Doppelpendels untersuchen und die Abhängigkeit von den Anfangsbedingungen bei festen Massen $m_1=1$ und $m_2=1$ und Pendellängen $l_1=1$ und $l_2=1$ betrachten. Wir werden im Folgenden sehen, dass die Energie des Systems einen bedeutenden Stellenwert bei der Untersuchung der Bewegung des Doppelpendels spielen wird und bei geringer und ganz hoher Gesamtenergie reguläre Bewegungen auftreten, wohingegen in einem mittleren Energiebereich chaotische Dynamiken vorherrschen.
Reguläre Bewegungen bei geringer Energie
Wir starten unsere Diskussion bei sehr kleinen Gesamtenergien. Als Anfangswert zur Zeit $t=0$ betrachten wir das Pendel zunächst als ruhend, wobei wir die beiden Massen nur geringfügig aus der Nulllage auslenken ($\theta_1(0) = \pi/14$ , $\theta_2(0) = \sqrt{2} \cdot \theta_1(0)$ und $\dot{\theta}_1(0) = \dot{\theta}_2(0) = 0$). Diese Auslenkung bewirkt, dass unser System am Anfang nur potentielle und keine kinetische Energie besitzt ($E_0 = V(0) \approx 0.9818$ und $T(0)=0$). Wir lösen das Anfangswertproblem im Bereich $t \in [0,15]$ unter Verwendung von $N=10000$ zeitlichen Gitterpunkten. Die nebenstehende Animation verdeutlicht die Bewegung des Doppelpendels und zeigt zusätzlich die entstehende Phasenraumtrajektorie des ersten Pendels. Anhand dieser regulären Bewegung erkennt man, dass die beiden Pendel in gleicher Richtung schwingen und sich die potentielle und kinetische Energie periodisch austauscht. Wir möchten nun noch weitere Simulationen bei gleicher Energie $E_0 \approx 0.9818$ machen, um zu sehen, ob bei dieser Energie ausschließlich reguläre Bewegungen entstehen.
Dazu betrachten wir uns den Ausdruck der Gesamtenergie $E_0 = E(\theta_1,\theta_2,\dot{\theta}_1,\dot{\theta}_2)$. Bei gegebenen Parameterwerten $m_1, m_2, l_1, l_2$ und $g$ muss man nun die Anfangsbedingungen $\theta_1(t_0),\theta_2(t_0),\dot{\theta}_1(t_0)$ und $\dot{\theta}_2(t_0)$ so wählen, dass der vorgegebene Energiewert $E_0=0.9818$ eingehalten wird. Nimmt man z.B. an, dass beide Massen sich in Ruhelage befinden ($\theta_1=\theta_2=0$) und lediglich die zweite Masse (das zweite Pendel) zur Zeit $t=0$ aus der Ruhelage angestoßen wird ($\dot{\theta}_1=0$) so kann man die Energie-Gleichung nach $\dot{\theta}_2$ umformen $\rightarrow \,\, \dot{\theta}_2 \approx 1.40126$ . Man erhält so eine weitere Anfangsbedingung, die mit dem vorgegebenen Energiewert kompatibel ist. Die nebenstehende Animation verdeutlicht wieder die Bewegung des Doppelpendels und zeigt zusätzlich die entstehende Phasenraumtrajektorie des ersten Pendels. Man erkennt, dass diese Bewegung zwar komplizierter erscheint, aber anscheinend keinen chaotischen Charakter besitzt. Um die Frage nach einem möglichen chaotischen Verhalten der Bewegung näher zu betrachten, werden wir uns im Folgenden die Trajektorie der Simulation im Phasenraum ansehen und die Schnittpunkte zur Hyperfläche $\theta_2=0$ (bzw. $\theta_1=0$) erstellen (Poincaré Abbildung oder Poincaré-Schnitt).
Die Poincaré Abbildung
Wir werden nun für die zweite Simulation eine Poincaré Abbildung anfertigen und speziell den Poincaré-Schnitt bei $\theta_2=0$ betrachten. Zusätzlich wollen wir nur die Poincaré-Punkte berücksichtigen, bei welchen die Trajektorie des zweiten Pendels die $\theta_2=0$-Ebene der Hypersphäre des Phasenraumes mit positiver Geschwindigkeit in x-Richtung durchstösst. Bei $\theta_2=0$ gilt für die Geschwindigkeit des zweiten Pendels in x-Richtung $\dot{x}(t)= l_1\,\hbox{cos}(\theta_1) \, \dot{\theta}_1 + l_1\,\dot{\theta}_2$ und wir haben somit die folgenden Bedingungen bei unserem Poincaré-Schnitt $$ \begin{equation} \theta_2(t)=0 \quad \hbox{und} \quad l_1\,\hbox{cos}(\theta_1(t)) \, \dot{\theta}_1(t) + l_1\,\dot{\theta}_2(t) > 0 \quad \forall \, t \in {\cal T} = [t_1,t_2,...,t_n] \quad, \end{equation} $$ wobei ${\cal T}$ die Menge der Zeitpunkte ist, bei denen die Trajektorie die ($\theta_2=0$) - Ebene in positiver Richtung durchläuft. Um die Vorgehensweise einer Poincaré-Abbindung zu verdeutlichen, berechnen wir nun diese Poincaré-Punkte und stellen sie zusammen mit der Phasenraumtrajektorie im dreidimensionalen Raum dar (näheres siehe Jupyter Notebook Das Doppelpendel).
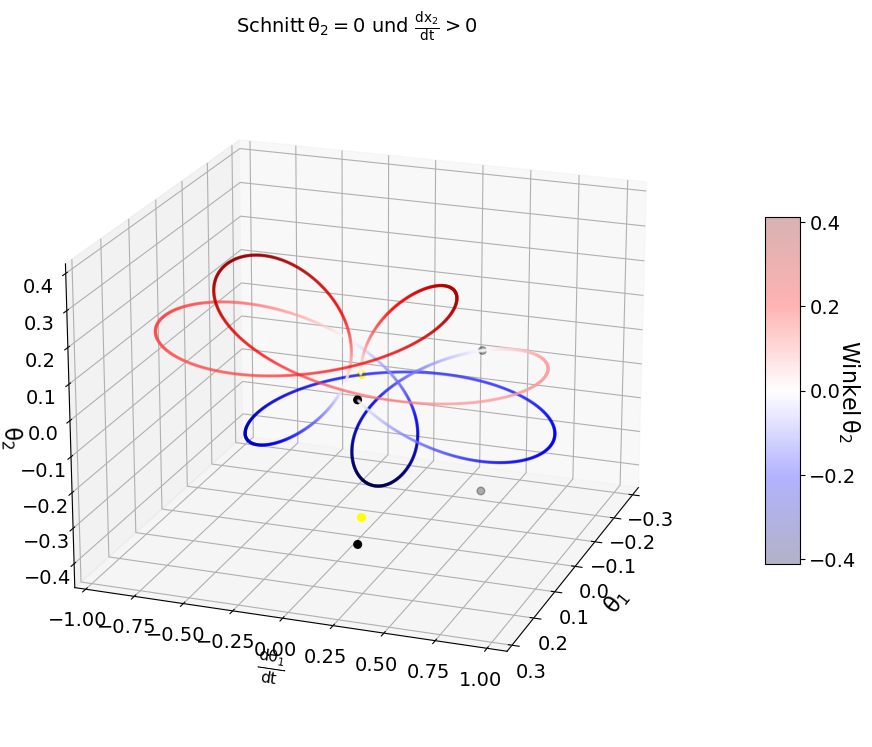
Die beiden oberen Abbildungen zeigen die Phasenraumtrajektorie in einem dreidimensionalen Koordinatensystem $(x,y,z) \rightarrow (\theta_1 , \frac{d \theta_1}{dt} , \theta_2)$. Die Farbskala der Trajektorien ist so gewählt, dass positive $\theta_2$-Werte rot und negative blau erscheinen, sodass der Übergang von blau zu rot gerade die Poincaré-Bedingung ( $\theta_2(t)=0 \, , \, l_1\,\hbox{cos}(\theta_1(t)) \, \dot{\theta}_1(t) + l_1\,\dot{\theta}_2(t) > 0$) repräsentiert. In der linken oberen Abbildung ist die Trajektorie lediglich bis zum zweiten Poincaré-Punkt gezeichnet, wobei der Anfangswert der Trajektorie als gelber Punkt und die beiden Poincaré-Punkte als schwarze Punkte auf der Trajektorie markiert sind. Zusätzlich ist auch die Projektion der Punkte auf die untere $(\theta_1 , \frac{d \theta_1}{dt})$-Ebene in den Grafiken visualisiert.
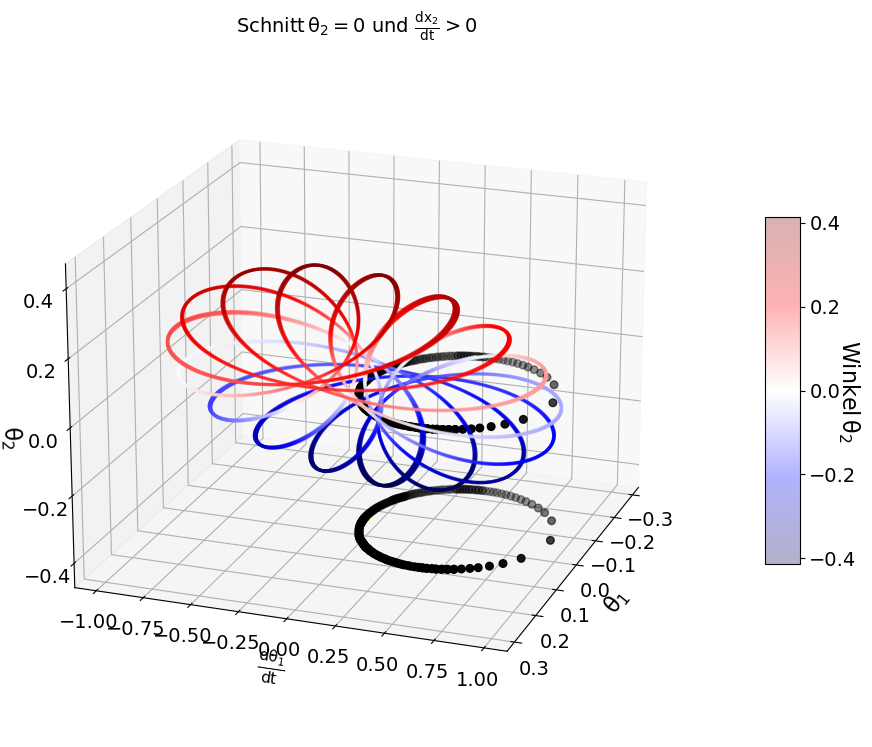
Um eine aussagekräftige Poincaré-Abbildung zu erhalten, muss man jedoch eine längere Simulation durchführen. In der rechten oberen Abbildung wurde deshalb der Endwert der Simulation auf $t_{end}=500$ erhöht, jedoch haben wir, der Übersichtlichkeit halber, die Trajektorie nur bis zum zehnten Poincaré-Punkt dargestellt. Betrachtet man sich Trajektorien und Poincaré-Schnitte zu längeren Zeiten, dann entsteht in der $(\theta_1 , \frac{d \theta_1}{dt})$-Ebene eine geometrische Form der Punkte (ein einzelner Punkt, eine Kurve oder ein begrenzter Flächenbereich), wobei reguläre (nicht-chaotische Bewegungen) durch einen Punkt oder eine Kurve gekennzeichnet sind. Man erkennt gut, dass in unserem Fall die Poincaré-Abbildung der Simulation eine Kurve liefert, was einer nicht-chaotischen Bewegung entspricht.
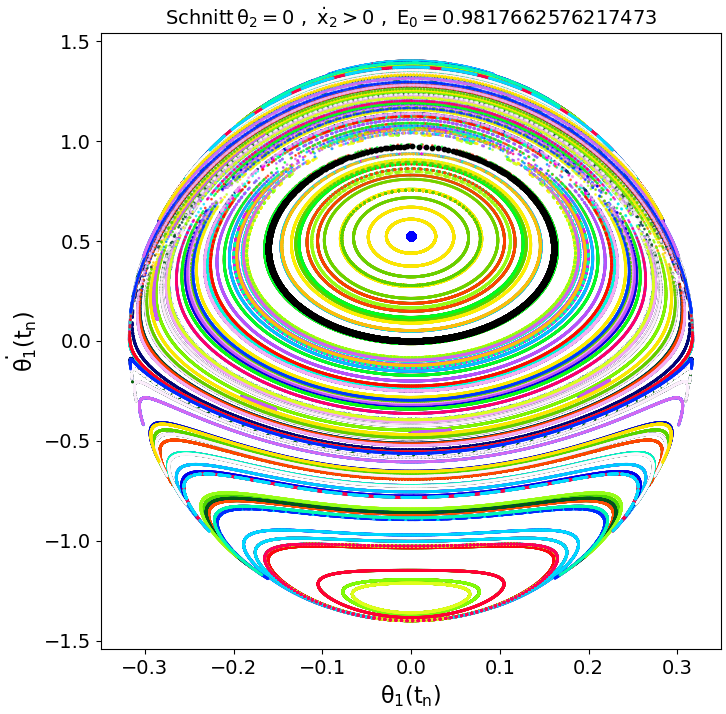
Für eine wissenschaftliche Analyse muss man jedoch noch viele weitere Anfangsbedingungen untersuchen, was in dem Jupyter Notebook mittels Python sehr zeitintensiv wäre. Die Abbildung auf der linken Seite wurde mit einem entsprechenden parallelisierten C++ Programm erzeugt (Doppelpendel_pschnitt_omp.cpp), welches wir am Ende diskutieren werden. Die Grafik zeigt den Poincaré-Schnitt bei der Gesamtenergie von $E_0 = 0.9817662576217473$ für sehr viele (ca. 350) unterschiedliche Anfangsbedingungen. Die schwarze, ein wenig dickere kreisförmige Punkte-Kurve, stellt den Poincaré-Schnitt der oben diskutierten Bewegung der zweiten Simulation dar und der blaue Punkt im Zentrum repräsentiert den Poincaré-Schnitt der ersten Simulation.
Reguläre und chaotische Bewegungen bei mittlerer Energie
Wir werden nun die Bewegung des Doppelpendels bei höheren Gesamtenergien studieren. Als Anfangswert zur Zeit $t=0$ betrachten wir wieder das Pendel als ruhend, wobei wir die beiden Massen nun ein wenig mehr aus der Nulllage auslenken ($\theta_1(0) = \pi/4$ , $\theta_2(0) = \sqrt{2} \cdot \theta_1(0)$ und $\dot{\theta}_1(0) = \dot{\theta}_2(0) = 0$). Wieder besitzt unser System am Anfang nur potentielle und keine kinetische Energie ($E_0 = V(0) \approx 11.2$ und $T(0)=0$). Wieder lösen das Anfangswertproblem im Bereich $t \in [0,15]$ unter Verwendung von $N=10000$ zeitlichen Gitterpunkten. Die untere Animation auf der linken Seite verdeutlicht die Bewegung des Doppelpendels und zeigt diesmal die entstehende Phasenraumtrajektorie des zweiten Pendels. Es handelt sich wieder um eine reguläre Bewegung und man erkennt, dass die beiden Pendel wieder in gleicher Richtung schwingen und sich die potentielle und kinetische Energie periodisch austauscht.
Die untere Animation auf der rechten Seite verdeutlicht hingegen eine chaotische Bewegung des Doppelpendels. Obwohl die Anfangskonfiguration ebenfalls den gleichen Wert an potentieller Energie besitzt ($E_0 = V(0) \approx 11.2$ und $T(0)=0$), erscheint die Bewegung viel chaotischer. Es wurde hierbei am Anfang lediglich das zweite Pendel aus seiner Ruhelage ausgelenkt ($\dot{\theta}_1=\dot{\theta}_2=\theta_1=0 \, , \quad \theta_2=1.71304617704556$). Um zu zeigen, dass es sich bei der Bewegung unten rechts wirklich um ein chaotisches Verhalten handelt, betrachten wir im Folgenden wieder die Poincaré Abbildungen der Bewegungen.
Die Poincaré Abbildung
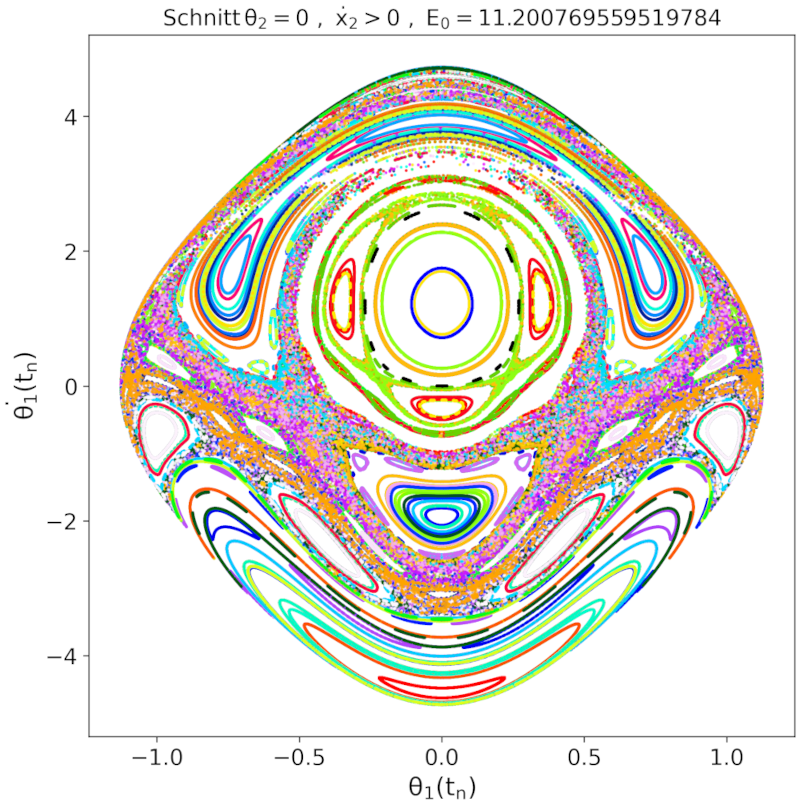
Unsere Vermutung, dass die zweite Simulation (Abbildung oben rechts) ein chaotisches Verhalten zeigt, bestätigt sich auch beim Betrachten ihres Poincaré-Schnitts. Dies zeigt auch die untere linke Grafik, welche auch mit dem parallelisierten C++ Programm (Doppelpendel_pschnitt_omp.cpp) erzeugt wurde. Die orangen, verteilten Poincaré-Punkte zeigen die Simulationsergebnisse der zweiten Simulation mit $E_0 = \approx 11.2$. Man erkennt, dass diese eine begrenzte Fläche ausfüllen, was bei chaotischen Bewegungen und seltsamen Attraktoren üblich ist. Die erste, reguläre Simulation ist hingegen die blaue, kreisförmige Kurve im Zentrum. Neben diesen beiden Anfangsbedingungen zeigt der Poincaré-Schnitt auf der linken Seite noch viele weitere Anfangsbedingungen, die mit der Gesamtenergie von $E_0\approx11.2$ kompatibel sind. Man erkennt eine komplizierte Struktur von regulären und chaotischen Bereichen.
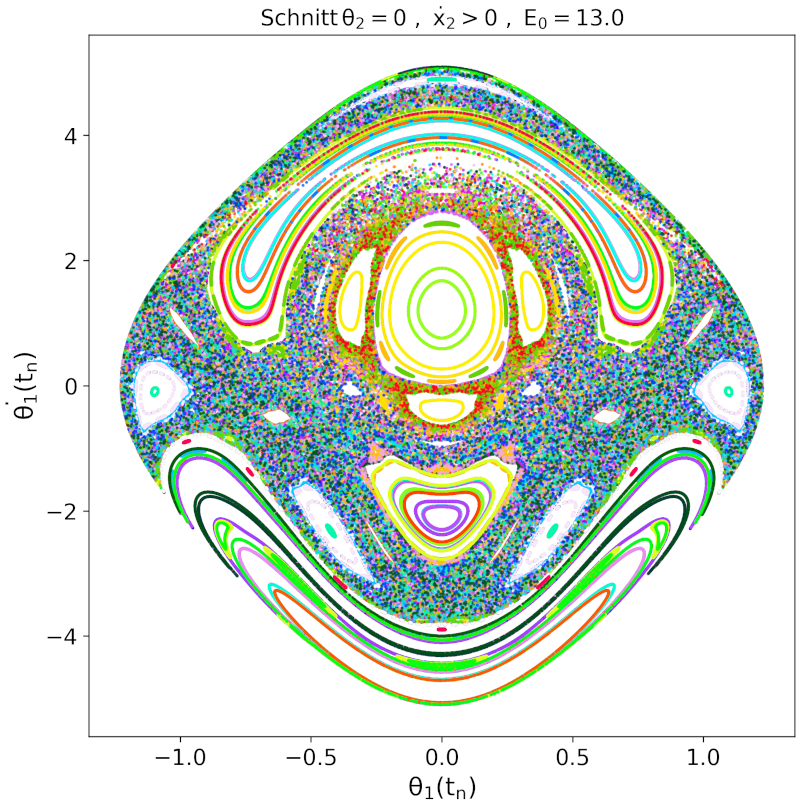
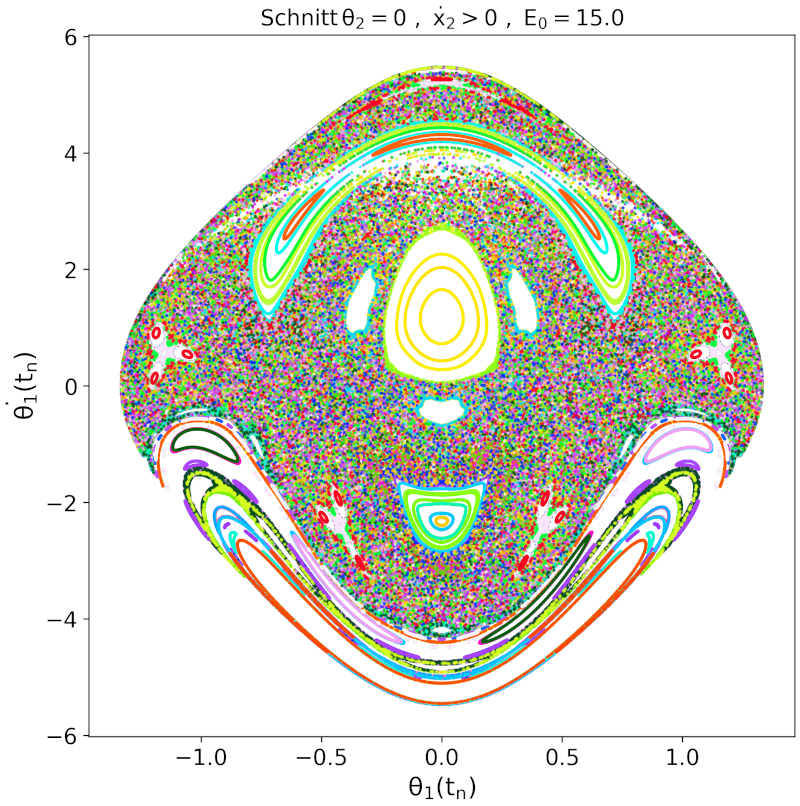
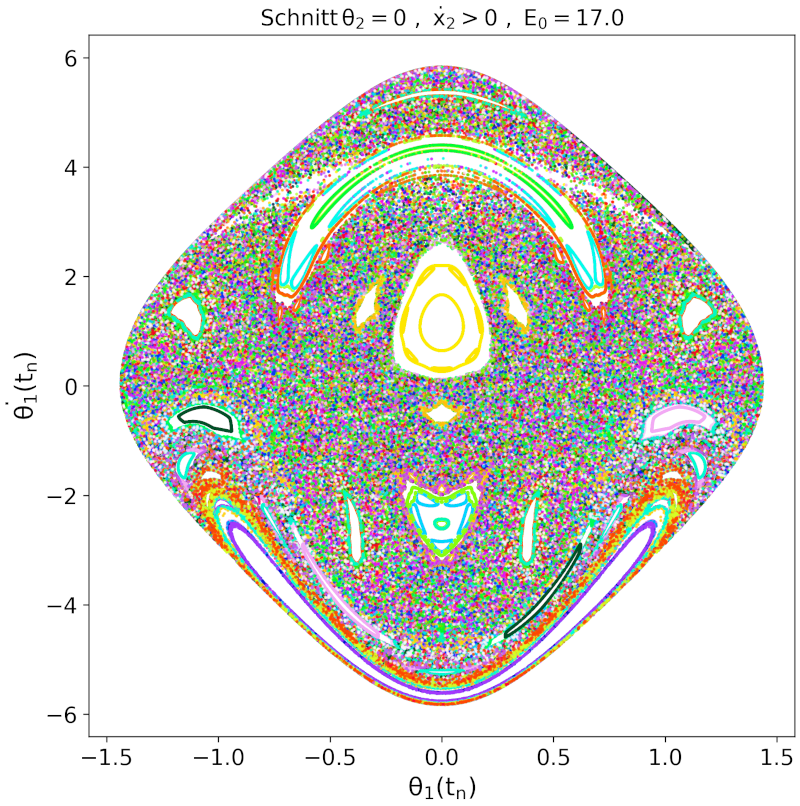
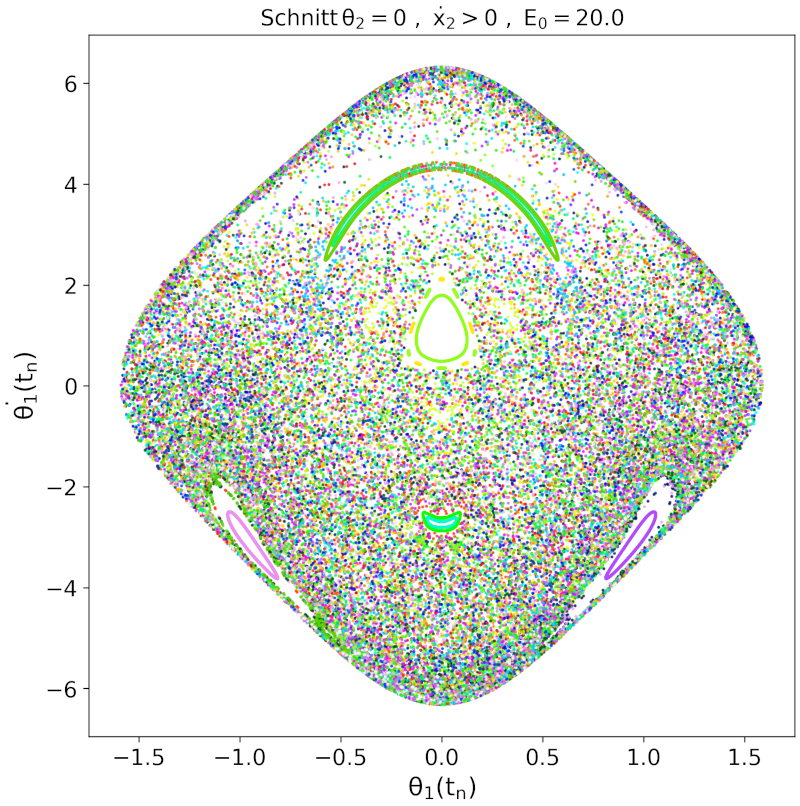
Erhöht man die Energie weiter, so dehnen sich die chaotischen Bereiche weiter aus und reguläre Bewegungen werden untypischer. Die obere Abbildung zeigt den Poincaré-Schnitt bei einer Energie von $E_0 = 13$ und die unteren drei Grafiken jeweils $E_0 = 15$ (links), $E_0 = 17$ (mitte) und $E_0 = 20$ (rechts).
Chaotische Bewegungen bei hoher Energie und Pendelüberschläge
Wir werden nun die Bewegung des Doppelpendels bei noch höheren Gesamtenergien studieren. Wieder betrachten wir zur Zeit $t=0$ das Pendel als ruhend, wobei wir die beiden Massen jetzt noch mehr aus der Nulllage auslenken. Speziell betrachten wir die folgenden beiden Anfangsbedingungen. Simulation 1: $\theta_1(0) = \pi/1.5$ , $\theta_2(0) = \sqrt{2} \cdot \theta_1(0)$, Simulation 2: $\theta_1(0) = \pi/1.5$ , $\theta_2(0) = - \sqrt{2} \cdot \theta_1(0)$, wobei bei beiden $\dot{\theta}_1(0) = \dot{\theta}_2(0) = 0$ gilt. Wieder besitzt somit unser System am Anfang nur potentielle und keine kinetische Energie ($E_0 = V(0) \approx 48.89$ und $T(0)=0$). Die unteren beiden Animationen zeigen die Bewegung der Doppelpendel und die entstehenden Phasenraumtrajektorien des zweiten Pendels. Bei beiden Simulationen überschlägt sich das zweite Pendel mehrfach, wobei in der zweiten Simulation sich das erste Pendel zusätzlich auch überschlägt. Bei solchen Bewegungen mit Überschlag werden die Phasenraumtrajektorien oft Modulo $2 \pi$ dargestellt. Diese Darstellungsart haben wir auch in den unteren Animationen verwendet.
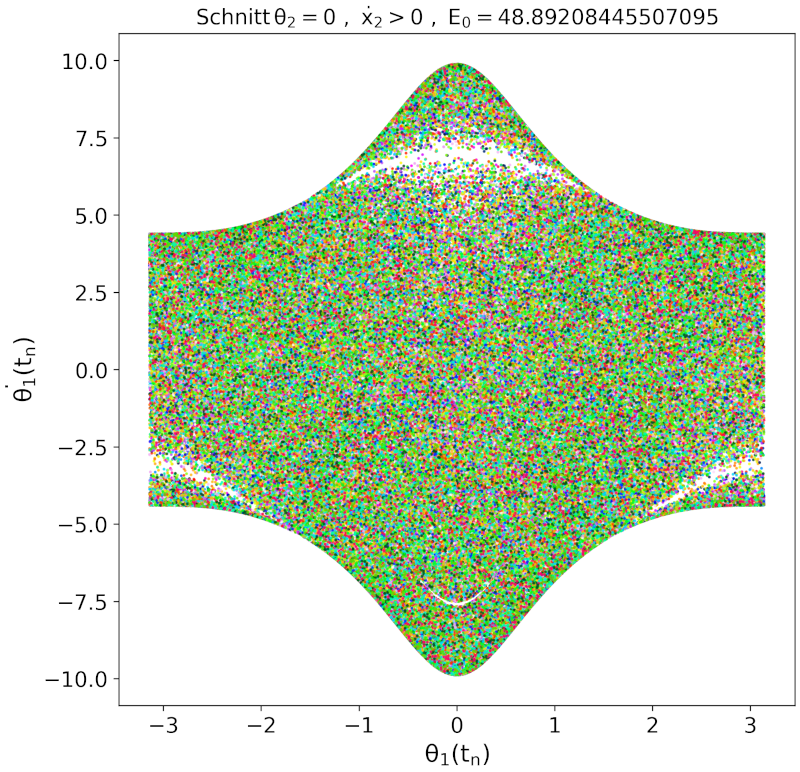
Beide Simulationen sehen sehr chaotisch aus, was auch der zugehörige Poincaré-Schnitt zeigt (siehe Abbildung rechts oben). Unsere Vermutung, dass bei dieser Gesamtenergie ($E_0 \approx 48.89$) stets ein chaotisches Verhalten erzeugt wird, bestätigt sich somit beim Betrachten des Poincaré-Schnitts. Reguläre Bewegungen scheinen bei dieser Energie so gut wie nicht möglich zu sein.
Erhöht man die Energie weiter, so entstehen bei sehr hohen Energien wieder Bereiche, die reguläre (nicht chaotische) Pendelbewegungen zeigen. Dies zeigen die weiteren Abbildungen.
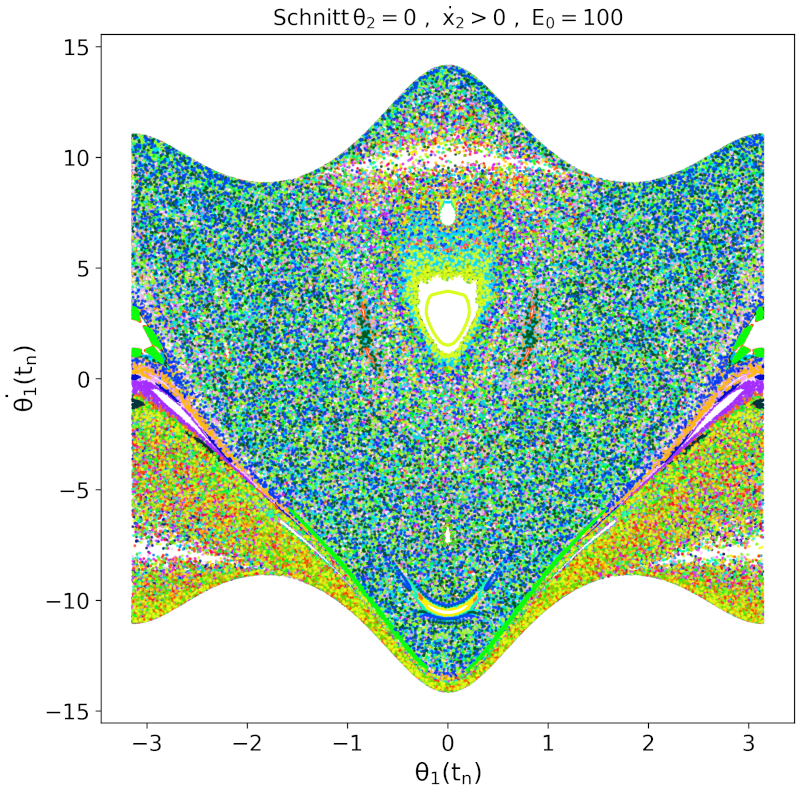
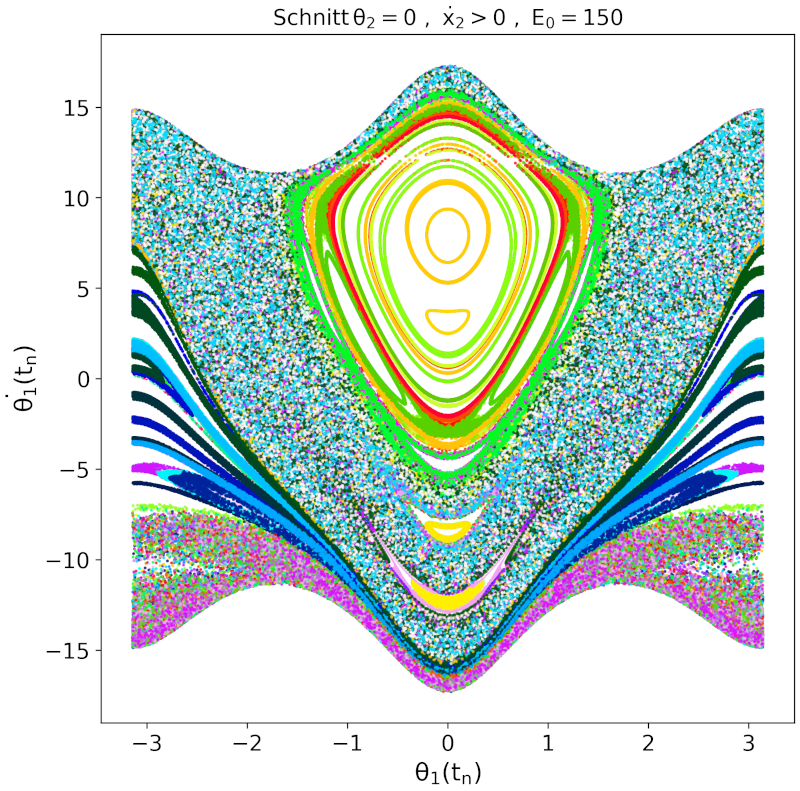
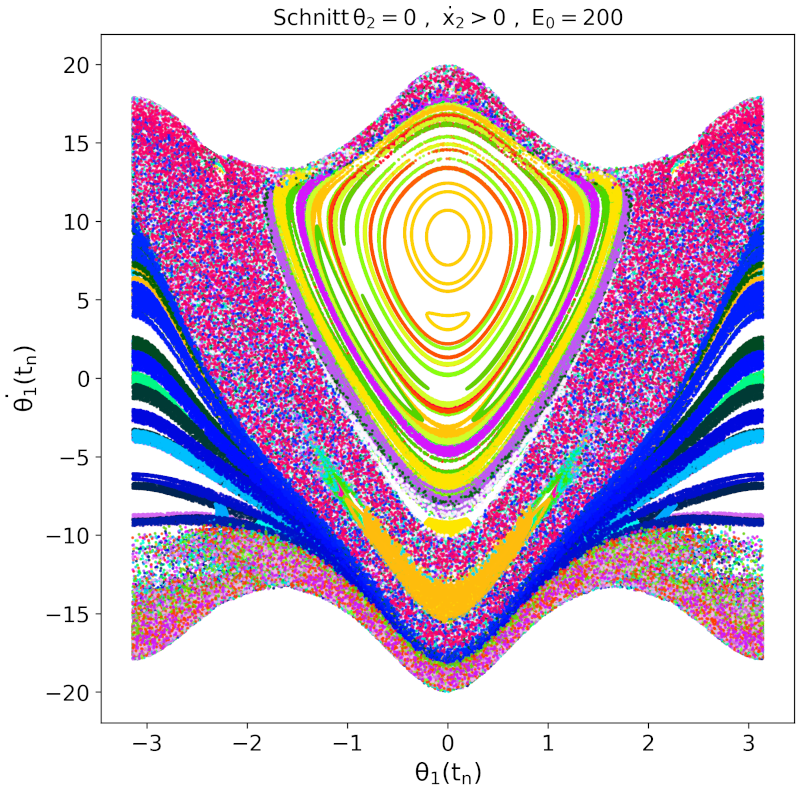
Berechnung der Poincaré Abbildungen: Das C++ Programm
Zur Berechnung der Poincaré Abbildungen wurde ein parallelisiertes C++ Programm (Doppelpendel_pschnitt_omp.cpp) verwendet, welches wir im Folgenden kurz vorstellen möchten. Es basiert auf dem Programm (Doppelpendel.cpp), welches wir schon weiter oben vorgestellt hatten, und besitzt das folgende Aussehen.
// Das Doppelpendel - Erstellung des Poincare-Schnitts bei fester Gesamtenergie /* Beispiel eines schwingenden Systems aus dem Bereich der Mechanik * welches bei gewissen Parameterkonstellationen deterministisch chaotische Bewegungen zeigt * Berechnung der Loesung eines Systems von Differentialgleichungen * mittels Runge-Kutta Ordnung vier Verfahren * Verfahren zur Loesung der DGL ist in einer Klasse ausgelagert * Zeitentwicklung, t-Werte in [a,b] * Konstruktor: dsolve(Anfangszeit a, Endzeit b, Anzahl der Punkte N, Anfangswerte alpha=y(a), DGL als Funktion, Laenge Pendel1, Laenge Pendel2) * Parallelisierung mittels OpenMP * Ausgabe zum Plotten mittels Python Skript plot_poincare.py: "./a.out > Doppelpendel_pschnitt.dat" */ #include <iostream> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <vector> // Vector-Container der Standardbibliothek #include <functional> // Funktionen in der Argumentenliste von Funktionen #include <omp.h> // OpenMP zum parallelen Rechnen using namespace std; // Benutze den Namensraum std // Klasse zum Loesen der DGL des Doppelpendels class dsolve{ //Definition der Klasse 'dsolve' double a = 0; // Untergrenze des Zeit-Intervalls [a,b] in dem die Loesung berechnet werden soll double b = 1; // Obergrenze des Intervalls [a,b] int N = 10; // Anzahl der Punkte in die das t-Intervall aufgeteilt wird vector<double> alpha = {0,0,0,0}; // Vier Anfangswerte (Ort und Geschwindigkeit der beiden Pendel) bei t=a vector<vector<double>> y_RungeK_4; // Deklaration einer double Vektor-Matrix zum speichern der Loesungen vector<double> Zeit; // Deklaration eines double Vektors zum speichern der Zeit-Werte public: // Konstruktor mit sieben Argumenten (Initialisierung der Parameter, Uebergabe der DGL als Funktion, Berechnung der Loesung der DGL) dsolve(double a_, double b_, unsigned int N_, vector<double> alpha_, function< vector<double>(double, vector<double>, double, double)> f, double l1, double l2) : a(a_),b(b_),N(N_),alpha(alpha_) { double h = (b - a)/N; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) int n = alpha_.size(); // Anzahl der Anfangswerte bzw. DGL-Gleichungen vector<double> k1(n),k2(n),k3(n),k4(n); // Deklaration der vier Runge-Kutta Parameter fuer jede Loesung vector<double> y(n); // Temporaerer Hilfsvektor Zeit.push_back(a_); // Zum Zeit-Vektor die Anfangszeit eintragen y_RungeK_4.push_back(alpha_); // Zum Loesungs-Vektor die Anfangswerte eintragen for(int i=0; i < N; ++i){ // for-Schleife ueber die einzelnen Punkte des t-Intervalls for(int j=0; j < n; ++j){k1[j] = h*f(Zeit[i],y_RungeK_4[i],l1,l2)[j];} // for-Schleife ueber die vier Runge-Kutta k1-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + k1[j]/2;} // Temporaerer Hilfsvektor for(int j=0; j < n; ++j){k2[j] = h*f(Zeit[i]+h/2,y,l1,l2)[j];} // for-Schleife ueber die vier Runge-Kutta k2-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + k2[j]/2;} // Temporaerer Hilfsvektor for(int j=0; j < n; ++j){k3[j] = h*f(Zeit[i]+h/2,y,l1,l2)[j];} // for-Schleife ueber die vier Runge-Kutta k3-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + k3[j];} // Temporaerer Hilfsvektor for(int j=0; j < n; ++j){k4[j] = h*f(Zeit[i]+h,y,l1,l2)[j];} // for-Schleife ueber die vier Runge-Kutta k4-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + (k1[j] + 2*k2[j] + 2*k3[j] + k4[j])/6;} // Temporaerer Hilfsvektor y_RungeK_4.push_back(y); // Zum Loesungs-Vektor den neuen Wert eintragen Zeit.push_back(a + (i+1)*h); // Zum Zeit-Vektor die neue Zeit eintragen } // Ende for-Schleife ueber die einzelnen Punkte des t-Intervalls }; // Ende des Konstruktors const vector<vector<double>>& get_y() const { return y_RungeK_4; } // Definition der konstanten Member-Funktion get_y(), Rueckgabewert Vektor-Matrix der Loesung der DGL const vector<double>& get_zeit() const { return Zeit; } // Definition der konstanten Member-Funktion get_zeit(), Rueckgabewert vector der zeit-Punkte }; // Ende der Klasse // Definition der Bewegungsgleichung des Doppelpendels vector<double> dgls(double t, vector<double> u_vec, double l1, double l2){ // Laenge Pendel1 l1, Laenge Pendel2 l2 double g {9.81}; // Erdbeschleunigung double m1 {1.0}; // Masse Pendel 1 double m2 {1.0}; // Masse Pendel 2 vector<double> du_dt; du_dt.push_back(u_vec[2]); // Vier DGLs erster Ordnung du_dt.push_back(u_vec[3]); // eigentliche Bewegungsgleichung folgt du_dt.push_back((g*m1*sin(u_vec[0]) + g*m2*sin(u_vec[0])/2 + g*m2*sin(u_vec[0] - 2*u_vec[1])/2 + l1*m2*pow(u_vec[2],2)*sin(2*u_vec[0] - 2*u_vec[1])/2 + l2*m2*pow(u_vec[3],2)*sin(u_vec[0] - u_vec[1]))/(l1*(-m1 + m2*pow(cos(u_vec[0] - u_vec[1]),2) - m2))); du_dt.push_back((-g*m1*sin(u_vec[1]) + g*m1*sin(2*u_vec[0] - u_vec[1]) - g*m2*sin(u_vec[1]) + g*m2*sin(2*u_vec[0] - u_vec[1]) + 2*l1*m1*pow(u_vec[2],2)*sin(u_vec[0] - u_vec[1]) + 2*l1*m2*pow(u_vec[2],2)*sin(u_vec[0] - u_vec[1]) + l2*m2*pow(u_vec[3],2)*sin(2*u_vec[0] - 2*u_vec[1]))/(2*l2*(m1 - m2*pow(cos(u_vec[0] - u_vec[1]),2) + m2))); return du_dt; // Rueckgabewert der DGLs als Standard-Vektor } // Ende: Definition der Bewegungsgleichung-Funktion // Vektorwertige Funktion, Rueckgabe von zwei Werten der Winkelgeschwindigkeit bei fester Gesamtenergie E0 vector<double> calc_d_theta2(double theta1, double theta2, double d_theta1, double E0, double l1, double l2) { double g {9.81}; // Erdbeschleunigung double m1 {1.0}; // Masse Pendel 1 double m2 {1.0}; // Masse Pendel 2 vector<double> d_theta2 = {0.0,0.0}; // Zwei Winkelgeschwindigkeiten des zweiten Pendels // Ausdruck unter der Wurzel (Ausdruck mittels Python Jupyter Notebook Doppelpendel.ipynb berechnet) double under_sqrt = E0 - 0.5*pow(d_theta1, 2)*pow(l1, 2)*m1 + 0.5*pow(d_theta1, 2)*pow(l1, 2)*m2*pow(cos(theta1 - theta2), 2) - 0.5*pow(d_theta1, 2)*pow(l1, 2)*m2 + g*l1*m1*cos(theta1) - g*l1*m1 + g*l1*m2*cos(theta1) - g*l1*m2 + g*l2*m2*cos(theta2) - g*l2*m2; if (under_sqrt >= 0) { // Festlegung der Winkelgeschwindigkeiten falls die Loesungen reell sind, sonst Rueckgabe {0.0,0.0} d_theta2 = {- d_theta1*l1*cos(theta1 - theta2)/l2 + sqrt(2.0)*sqrt(under_sqrt)/(l2*sqrt(m2)) , - d_theta1*l1*cos(theta1 - theta2)/l2 - sqrt(2.0)*sqrt(under_sqrt)/(l2*sqrt(m2)) }; } // Ende der if-Auswahlanweisung return d_theta2; // Rueckgabewert der zwei Loesungen als Standard-Vektor } // Vektor-Matrixwertige Funktion, Erzeugung und Rueckgabe mehrerer Anfangsbedingungen bei fester Gesamtenergie E0 vector<vector<double>> Erzeug_Anfangsb(double E0, int grid_size, double l1, double l2) { vector<vector<double>> Anfangsb; // Deklaration einer double Vektor-Matrix zum speichern der Anfangsbedingungen double d_theta2_lim = calc_d_theta2(0.0,0.0,0.0,E0,l1,l2)[0]; // Maximal moeglicher Wert der Winkelgeschwindigkeit des zweiten Pendels (E0=E_kin von Pendel 2) double theta1_lim = M_PI; // Definition, maximal moeglicher Wert des Winkels des ersten Pendels // Festlegung des maximal moeglichen Wert des Winkels des ersten Pendels for (int i = 0; i < 300; ++i) { double theta1 = i * M_PI/300.0; vector<double> d_theta2 = calc_d_theta2(theta1,0.0,0.0,E0,l1,l2); if ( d_theta2[0] != 0.0 ) { theta1_lim = theta1; } } // Erzeugung der Anfangsbedingungen (maximal grid_size*grid_size Werte) for (int i = 0; i < grid_size; ++i) { // for-Schleife ueber die einzelnen Punkte der Winkel des ersten Pendels double theta1 = - theta1_lim + i * theta1_lim/grid_size*2.0; // theta1-Werte in [-theta1_lim , theta1_lim] for (int j = 0; j < grid_size; ++j) { // for-Schleife ueber die einzelnen Punkte der Winkelgeschwindigkeit des ersten Pendels double d_theta1 = - d_theta2_lim + j * d_theta2_lim/grid_size*2.0; // theta1-Werte in [-theta2_lim , theta2_lim] vector<double> d_theta2 = calc_d_theta2(theta1,0.0,d_theta1,E0,l1,l2); // Berechnung der zwei Loesungen der Winkelgeschwindigkeiten bei theta2==0 und E0 if ( d_theta2[0] != 0.0 ) { // Falls die Loesungen reell sind werden sie zur Vektor-Matrix der Anfangsbedingungen hinzugefuegt Anfangsb.push_back({theta1, 0.0, d_theta1, d_theta2[0]}); // Anfangsbedingung, Loesung 1 Anfangsb.push_back({theta1, 0.0, d_theta1, d_theta2[1]}); // Anfangsbedingung, Loesung 2 } // Ende der if-Auswahlanweisung } // Ende for-Schleife grid 2 } // Ende for-Schleife grid 1 return Anfangsb; // Rueckgabewert der Anfangsbedingungen als Vektor-Matrix } // Funktion um bei Ueberschlaegen des Pendels den Winkel wieder in den Bereich [-pi,pi] zu verschieben double wrap_angle(double angle) { double wrapped = fmod(angle + M_PI, 2.0 * M_PI); // Verschiebt in [0,2*pi] und wendet Modulo an if (wrapped < 0) wrapped += 2.0 * M_PI; // Korrigiert negative Werte return wrapped - M_PI; // Verschiebt zurück in [-pi,pi] } // Struktur zum Speichern eines Poincare-Punkts struct PoincarePoint { double t_cross; // Zeitpunkt des Schnitts double theta1; // Winkel theta1 double theta2; // Winkel theta2 (hier immer 0) double d_theta1; // Winkelgeschwindigkeit dtheta1 double d_theta2; // Winkelgeschwindigkeit dtheta2 }; // Hauptfunktion int main(){ double E0 = 15.0; // Deklaration und Initialisierung der Gesamtenergie double l1 = 1.0, l2 = 1.0; // Parameterwerte des Doppelpendels double t_end = 3000; // Obergrenze des t-Intervalls [0,t_end] unsigned int Anz_Punkte = 500000; // Anzahl der Punkte in die das t-Intervall aufgeteilt wird int grid_size = 15; // Gittergroesse zur Erzeugung der Anfangsbedingungen (maximal grid_size*grid_size Werte) vector<vector<double>> Anfangsb = Erzeug_Anfangsb(E0,grid_size,l1,l2); // Deklaration einer double Vektor-Matrix zum speichern der unterschiedlichen Anfangsbedingungen vector<vector<PoincarePoint>> pschnitt_wert(Anfangsb.size()); // Deklaration einer double Vektor-Matrix zum speichern der Loesungen der Punkte des Poincare-Schnitts // for-Schleife ueber unterschiedliche Anfangsbedingungen (mit OpenMP-Parallelisierung) #pragma omp parallel for for (int n=0; n < Anfangsb.size(); ++n) { // Pendel-Konstruktor (Zeit-Intervall: [0,t_end], Anzahl der Zeit-Punkte: Anz_Punkte, Anfangsorte und Geschwindigkeiten: {0,0,0,0}, DGL,Laenge Pendel 1,Laenge Pendel 2) dsolve Loes {0,t_end,Anz_Punkte,Anfangsb[n],dgls,l1,l2}; vector<PoincarePoint> pschnitt_wert_n; // Lokaler Vektor fuer jeden Thread for(int i=0; i < Loes.get_zeit().size()-1; ++i){ // for-Schleife zur Terminalausgabe; Zeitwerte double theta2_w = wrap_angle(Loes.get_y()[i][1]); // Winkel bei Ueberschlaegen wieder in den Bereich [-pi,pi] zu verschieben double theta2_wd = wrap_angle(Loes.get_y()[i+1][1]); // Winkel bei Ueberschlaegen wieder in den Bereich [-pi,pi] zu verschieben if (theta2_w * theta2_wd < 0 && l2*Loes.get_y()[i][3] +l1*Loes.get_y()[i][2]*cos(Loes.get_y()[i][0]) > 0 && abs(theta2_w) < 1){ // if-Anweisung, theta2 == 0, dx2 > 0 double t_cross = Loes.get_zeit()[i] - theta2_w * (Loes.get_zeit()[i+1] - Loes.get_zeit()[i]) / (theta2_wd - theta2_w); // Interpolationen double theta1_cross = Loes.get_y()[i][0] + (Loes.get_y()[i+1][0] - Loes.get_y()[i][0]) * (t_cross - Loes.get_zeit()[i]) / (Loes.get_zeit()[i+1] - Loes.get_zeit()[i]); double d_theta1_cross = Loes.get_y()[i][2] + (Loes.get_y()[i+1][2] - Loes.get_y()[i][2]) * (t_cross - Loes.get_zeit()[i]) / (Loes.get_zeit()[i+1] - Loes.get_zeit()[i]); double d_theta2_cross = Loes.get_y()[i][3] + (Loes.get_y()[i+1][3] - Loes.get_y()[i][3]) * (t_cross - Loes.get_zeit()[i]) / (Loes.get_zeit()[i+1] - Loes.get_zeit()[i]); double theta1_wrapped = wrap_angle(theta1_cross); // Winkel bei Ueberschlaegen wieder in den Bereich [-pi,pi] zu verschieben pschnitt_wert_n.push_back({t_cross, theta1_wrapped, 0.0, d_theta1_cross, d_theta2_cross} ); // Fuellen des lokalen Vektors der Poincare-Punkte der n-ten Anfangsbedingung } // Ende der if-Auswahlanweisung } // Ende der for-Schleife, Zeitwerte pschnitt_wert[n] = pschnitt_wert_n; // Fuellen der Vektor-Matrix der Poincare-Punkte } // Ende der for-Schleife, Anfangsbedingungen printf("# 0: Anfbed i \n# 1: t-Wert \n# 2: theta_1 \n# 3: theta_2 \n# 4: d_theta_2 \n# 5: d_theta_2 \n"); // Beschreibung der ausgegebenen Groessen for(int n=0; n < Anfangsb.size(); ++n){ // for-Schleife zur Terminalausgabe, unterschiedliche Anfangsbedingungen for(const auto& p : pschnitt_wert[n]){ // for-Schleife zur Terminalausgabe, Poincare-Punkte der n-ten Anfangsbedingung printf("%3d ", n); printf("%19.15f %19.15f %19.15f %19.15f %19.15f \n", p.t_cross, p.theta1, p.theta2, p.d_theta1, p.d_theta2); } // Ende for-Schleife, Poincare-Punkte der n-ten Anfangsbedingung } // Ende for-Schleife, unterschiedliche Anfangsbedingungen } // Ende der Hauptfunktion
Unterhalb der Klasse 'dsolve' und der Funktion 'dgls', aber außerhalb der Hauptfunktion sind mehrere Funktionen dem Programm hinzugefügt worden. Die Funktion 'calc_d_theta2' wurde mittels des Jupyter Notebook Das Doppelpendel generiert und sie berechnet, falls möglich, zwei Lösungen der Winkelgeschwindigkeiten des zweiten Pendels bei fester Gesamtenergie $E_0$. Diese Funktion wird dann innerhalb der Funktion 'Erzeug_Anfangsb' benutzt, die benutzt wird, um mehrere Anfangsbedingungen bei fester Gesamtenergie $E_0$ zu erzeugen. Weiter wird eine Funktion 'wrap_angle' definiert, die benutzt wird, um bei möglichen Pendelüberschlägen den Winkel wieder in den Bereich $[-\pi , \pi]$ zu verschieben. Schließlich wird noch eine Struktur 'struct PoincarePoint' erzeugt, die in komfortabler Weise die Variablen eines Poincaré-Punktes speichert.
In der Hauptfunktion des Programms werden zunächst die Anfangsbedingungen bei fester Gesamtenergie $E_0$ erzeugt, wobei der Phasenraum des ersten Pendels in eine Gitterstruktur unterteilt wurde (hier grid_size = 15) um die unterschiedlichen Bereiche des Poincaré-Schnitts abbilden zu können. In einer parallelisierten for-Schleife werden dann die einzelnen unabhängigen Simulationen der unterschiedlichen Anfangsbedingungen durchgeführt und die Poincaré-Punkte gespeichert. Am Ende werden dann die Lösungen in geordneter Weise ausgegeben.
Die berechneten Daten können dann mit dem folgenden Python Skript geplottet werden, wobei jede Anfangsbedingung eine unterschiedliche Farbe erhält.
import numpy as np import matplotlib.pyplot as plt import matplotlib params = { 'figure.figsize' : [8,8], 'axes.titlesize' : 14, 'axes.labelsize' : 16, 'xtick.labelsize' : 14 , 'ytick.labelsize' : 14 } matplotlib.rcParams.update(params) data = np.genfromtxt("./Doppelpendel_pschnitt.dat") plt.title(r"$\rm Schnitt \, \theta_2=0 \,\, , \,\, \dot{x}_2>0 \,\, , \,\, E_0 = 15$") plt.xlabel(r"$\rm \theta_1(t_n)$") plt.ylabel(r"$\rm \dot{\theta_1}(t_n)$") plt.scatter(data[:,2],data[:,4],c=data[:,0], cmap=plt.cm.gist_ncar, s=1, alpha=0.7) #Speichern der Bilder als (.png , benoetigt dvipng unter Linux)- und .pdf-Datei saveFig="./poincare_15.png" plt.savefig(saveFig, dpi=300,bbox_inches="tight",pad_inches=0.05,format="png") #saveFig = "./poincare_15.pdf" #plt.savefig(saveFig,bbox_inches="tight",pad_inches=0.05,format="pdf") plt.show()
