Die Achterbahn
Von der Euler-Lagrange Gleichung zur Bewegungsgleichung mittels SymPy
Wir berechnen zunächst auf analytischem Weg, unter Verwendung der SymPy Bibliothek, die Euler-Lagrange Gleichungen der Achterbahn und schreiben diese dann in ein System von erster Ordnung Differentialgleichungen um.
Das nebenstehende Python Jupyter Notebook 'Achterbahn.ipynb' (View Notebook, Download Notebook) stellt eine Musterlösung dieser ersten Teilaufgaben dar. Wir betrachten zunächst den Fall einer allgemeinen Funktion $h(x)$, definieren die nötigen SymPy-Symbole und SymPy-Funktionen und implementieren die Lagrangefunktion $L = T - V$ in der folgenden Form: $$ \begin{eqnarray} &T = \frac{1}{2} m \left[ \dot{x}(t)^2 + \dot{y}(t)^2 \right] = \frac{1}{2} m \, \dot{x}^2 \cdot \left[ 1 + \left( \frac{d h(x)}{dx} \right)^2 \right] &\\ &V(t) = m \, g \cdot y(t) = m \, g \cdot h(x(t)) & \end{eqnarray} $$ Mittels der Euler-Lagrange Gleichungen $$ \begin{equation} \frac{d }{dt} \left( \frac{\partial L}{\partial \dot{x}} \right) - \frac{\partial L}{\partial x} \, =\, 0 \end{equation} $$ erhält man die Bewegungsgleichung des betrachteten Systems. Die Bewegung des Wagens wird durch eine Differentialgleichung zweiter Ordnung bestimmt und diese hängt nicht mehr von dem Wert der Masse des Wagens ab. Wir formen die DGL in die übliche Form einer Differentialgleichung zweiter Ordnung um und erhalten: $$ \begin{equation} \ddot{x}(t) = \frac{d^{2}}{d t^{2}} x{\left (t \right )} = - \frac{\left(g + \frac{d^{2}}{d x^{2}} h{\left (x \right )} \left(\frac{d}{d t} x{\left (t \right )} \right)^{2}\right) \frac{d}{d x } h{\left (x \right )}}{\left(\frac{d}{d x } h{\left (x \right )}\right)^{2} + 1} = f(t,x,\dot{x}) \end{equation} $$
Setzt man nun die formbestimmende Funktion der Metallschiene der Achterbahn ( z.B. $h(x) = e^{\frac{\sqrt{x^2}}{10}} \cdot \left( \hbox{sin}\left( \frac{x^2}{10} \right) \right)^2$) ein, so erhält man mittels Sympy den in der folgenden Abbildung dargestellte Ausdruck für die DGL bestimmende Funktion $f(t,x,\dot{x})$.

Die obige Ausgabe verwendeten wir dann später im C++ Programm Achterbahn.cpp.
Um die entstandene DGL zweiter Ordnung numerisch lösen zu können, schreiben wir sie in ein System von zwei DGLs erster Ordnung um. Wir betrachten nun die numerische Lösung und machen die folgenden Variablenumbenennung: $u_1(t)=x(t)$, und $u_2(t)=\dot{x}(t)$ und definieren das System von DGLs wie folgt: $$ \begin{eqnarray} \dot{u_1}(t) &=& \frac{d u_1}{dt} = \frac{d x}{dt} = u_2(t) \\ \dot{u_2}(t) &=& \frac{d u_2}{dt} = \frac{d \dot{x}}{dt} = \ddot{x}(t) = f(u_1,u_2) = f(t,x,\dot{x}) \end{eqnarray} $$
Simulationsergebnisse
Die untere Animation stellt die Bewegung zweier Achterbahn-Wagen dar und die Simulationen wurden mit dem Python Jupyter Notebook 'Achterbahn.ipynb' (View Notebook, Download Notebook) erstellt. Der rote Wagen wurde dabei mit $\dot{x}(0) = 8.5$ [m/s] in die Bahn katapultiert und der grüne Wagen mit $\dot{x}(0) = 13.2$ [m/s].
Die Ergebnisse wurden dann mit den Berechnungen des C++ Programms Achterbahn.cpp verglichen. Als Vorlage verwenden wir dabei das im Projekt Die schwingende Kette erstellte Programm SchwingendeKette.cpp. In diesem objektorientierten C++ Programm hatten wir den Kern-Algorithmus der numerischen Lösung (Runge-Kutta Ordnung vier Verfahren) in einer C++ Klasse auslagern. Die Klasse 'dsolve' war dabei so allgemein gehalten, das sie die Berechnung der numerischen Lösung für eine beliebige Anzahl von gekoppelten Differentialgleichungen erster Ordnung generieren konnte. In dem folgenden Programm (Achterbahn.cpp) verwenden wir nun diese Klasse zum Simulieren der Bewegung des Achterbahn-Wagens.
/* Achterbahn: Bewegung eines Massenpunktes auf einer vorgegebenen Bahn * Berechnung der Loesung eines Systems von Differentialgleichungen * mittels Runge-Kutta Ordnung vier Verfahren * Verfahren zur Loesung der DGL ist in eine Klasse ausgelagert * Zeitentwicklung der fuer unterschiedliche t-Werte in [a,b] * Konstruktor: dsolve(Anfangszeit a, Endzeit b, Anzahl der Punkte N, Anfangswerte alpha=y(a), DGL als Funktion) * Ausgabe zum Plotten mittels Python Jupyter Notebook Achterbahn.ipynb: "./a.out > Achterbahn_low.dat */ #include <iostream> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <vector> // Vector-Container der Standardbibliothek #include <functional> // Funktionen in der Argumentenliste von Funktionen using namespace std; // Benutze den Namensraum std class dsolve{ //Definition der Klasse 'dsolve' double a = 0; // Untergrenze des Zeit-Intervalls [a,b] in dem die Loesung berechnet werden soll double b = 1; // Obergrenze des Intervalls [a,b] int N = 10; // Anzahl der Punkte in die das t-Intervall aufgeteilt wird vector<double> alpha = {1,0}; // Zwei Anfangswerte (Ort und Geschwindigkeit des Wagens) bei t=a vector<vector<double>> y_RungeK_4; // Deklaration eine double Vektor-Matrix zum speichern der Loesungen vector<double> Zeit; // Deklaration eines double Vektors zum speichern der Zeit-Werte public: // Konstruktor mit fuenf Argumenten (Initialisierung der Parameter, Uebergabe der DGL als Funktion, Berechnung der Loesung der DGL) dsolve(double a_, double b_, int N_, vector<double> alpha_, function< vector<double>(double, vector<double>)> f) : a(a_),b(b_),N(N_),alpha(alpha_) { double h = (b - a)/N; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) int n = alpha_.size(); // Anzahl der Anfangswerte bzw. DGL-Gleichungen vector<double> k1(n),k2(n),k3(n),k4(n); // Deklaration der vier Runge-Kutta Parameter fuer jede Loesung vector<double> y(n); // Temporaerer Hilfsvektor Zeit.push_back(a_); // Zum Zeit-Vektor die Anfangszeit eintragen y_RungeK_4.push_back(alpha_); // Zum Loesungs-Vektor die Anfangswerte eintragen for(int i=0; i < N; ++i){ // for-Schleife ueber die einzelnen Punkte des t-Intervalls for(int j=0; j < n; ++j){k1[j] = h*f(Zeit[i],y_RungeK_4[i])[j];} // for-Schleife ueber die Runge-Kutta k1-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + k1[j]/2;} // Temporaerer Hilfsvektor for(int j=0; j < n; ++j){k2[j] = h*f(Zeit[i]+h/2,y)[j];} // for-Schleife ueber die Runge-Kutta k2-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + k2[j]/2;} // Temporaerer Hilfsvektor for(int j=0; j < n; ++j){k3[j] = h*f(Zeit[i]+h/2,y)[j];} // for-Schleife ueber die Runge-Kutta k3-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + k3[j];} // Temporaerer Hilfsvektor for(int j=0; j < n; ++j){k4[j] = h*f(Zeit[i]+h,y)[j];} // for-Schleife ueber die Runge-Kutta k4-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + (k1[j] + 2*k2[j] + 2*k3[j] + k4[j])/6;} // Temporaerer Hilfsvektor y_RungeK_4.push_back(y); // Zum Loesungs-Vektor den neuen Wert eintragen Zeit.push_back(a + (i+1)*h); // Zum Zeit-Vektor die neue Zeit eintragen } // Ende for-Schleife ueber die einzelnen Punkte des t-Intervalls }; // Ende des Konstruktors const vector<vector<double>>& get_y() const { return y_RungeK_4; } // Definition der konstanten Member-Funktion get_y(), Rueckgabewert Vektor-Matrix der Loesung der DGL const vector<double>& get_zeit() const { return Zeit; } // Definition der konstanten Member-Funktion get_zeit(), Rueckgabewert vector der zeit-Punkte }; // Ende der Klasse // Definition der Bewegungsgleichung (Zwei DGLs erster Ordnung, siehe Jupyter Notebook Achterbahn.ipynb) vector<double> dgls(double t, vector<double> u_vec){ double g = 9.81; // Wert der Erbeschleunigung vector<double> du_dt; du_dt.push_back(u_vec[1]); du_dt.push_back(0.2*u_vec[0]*(-200.0*g*pow(u_vec[0], 2)*exp(0.316227766016838*fabs(u_vec[0]))*cos(0.1*pow(u_vec[0], 2)) - 158.11388300841898*g*exp(0.316227766016838*fabs(u_vec[0]))*sin(0.1*pow(u_vec[0], 2))*fabs(u_vec[0]) + 32.0*pow(u_vec[0], 4)*pow(u_vec[1], 2)*exp(0.63245553203367599*fabs(u_vec[0]))*pow(sin(0.1*pow(u_vec[0], 2)), 2)*cos(0.1*pow(u_vec[0], 2)) - 16.0*pow(u_vec[0], 4)*pow(u_vec[1], 2)*exp(0.63245553203367599*fabs(u_vec[0]))*cos(0.1*pow(u_vec[0], 2)) + 75.894663844041105*pow(u_vec[0], 2)*pow(u_vec[1], 2)*exp(0.63245553203367599*fabs(u_vec[0]))*pow(sin(0.1*pow(u_vec[0], 2 )), 3)*fabs(u_vec[0]) + 80.0*pow(u_vec[0], 2)*pow(u_vec[1], 2)*exp(0.63245553203367599*fabs(u_vec[0]))*pow(sin(0.1*pow(u_vec[0], 2)), 3) - 60.0*pow(u_vec[0], 2)*pow(u_vec[1], 2)*exp(0.63245553203367599*fabs(u_vec[0]))*pow(sin(0.1*pow(u_vec[0], 2)), 2)*cos(0.1*pow(u_vec[0], 2)) - 63.245553203367592*pow(u_vec[0], 2)*pow(u_vec[1], 2)*exp(0.63245553203367599*fabs(u_vec[0]))*sin(0.1*pow(u_vec[0], 2))*fabs(u_vec[0]) - 80.0*pow(u_vec[0], 2)*pow(u_vec[1], 2)*exp(0.63245553203367599*fabs(u_vec[0]))*sin(0.1*pow(u_vec[0], 2)) - 15.811388300841898*pow(u_vec[1], 2 )*exp(0.63245553203367599*fabs(u_vec[0]))*pow(sin(0.1*pow(u_vec[0], 2)), 3)*fabs(u_vec[0]) - 63.245553203367592*pow(u_vec[1], 2)*exp(0.63245553203367599*fabs(u_vec[0]))*pow(sin(0.1*pow(u_vec[0], 2)), 2)*cos(0.1*pow(u_vec[0], 2))*fabs(u_vec[0]))*sin(0.1*pow(u_vec[0], 2))/(100.0*pow(u_vec[0], 2) + 16.0*pow(pow(u_vec[0], 2)*cos(0.1*pow(u_vec[0], 2)) + 0.79056941504209488*sin(0.1*pow(u_vec[0], 2))*pow(fabs(u_vec[0]), 1.0), 2)*exp(0.63245553203367599*fabs(u_vec[0]))*pow(sin(0.1*pow(u_vec[0], 2)), 2))); return du_dt; // Rueckgabewert der DGLs als Standard-Vektor } // Ende: Definition der Bewegungsgleichung-Funktion // Hauptfunktion int main(){ dsolve Loes {0,15,10000,{0.01,13.2},dgls}; // Benutzt Konstruktor mit a=0, b=15, N=10000, Ort=0.01, Geschwindigkeit=13.2 printf("# 0: Index i \n# 1: t-Wert \n# 2: x \n# 3: v_x \n"); // Beschreibung der ausgegebenen Groessen for(size_t i=0; i < Loes.get_zeit().size(); ++i){ // for-Schleife zur Terminalausgabe; Zeitwerte printf("%3ld %19.15f %19.15f %19.15f \n",i, Loes.get_zeit()[i], Loes.get_y()[i][0], Loes.get_y()[i][1]); // Ausgabe } // Ende der for-Schleife } // Ende der Hauptfunktion
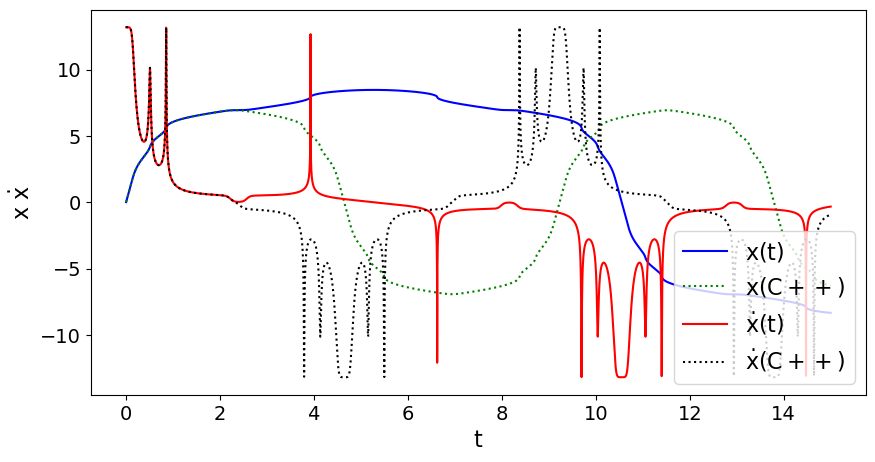
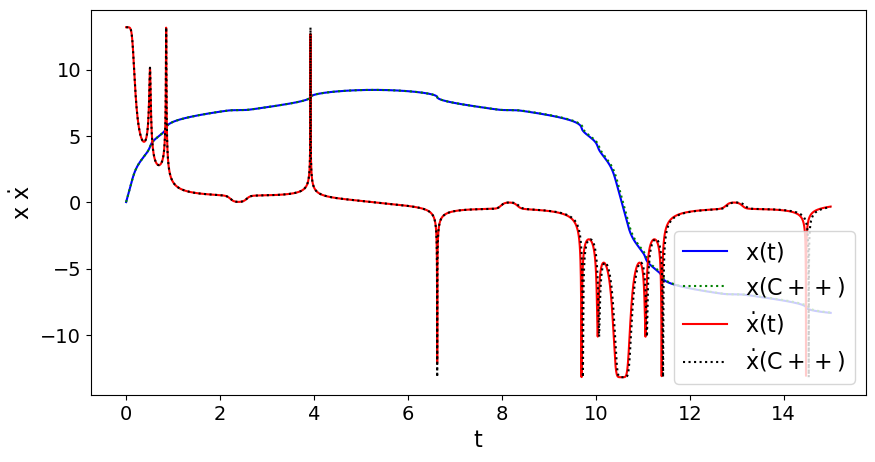
Die DGL bestimmende Funktion $f(t,x,\dot{x})$ exportierten wir uns dabei als C++ Quelltext vom Jupyter Notebook und fügten den Ausdruck in der Funktion 'vector<double> dgls(double t, vector<double> u_vec){ ...}' ein. Am Ende des Programms werden die berechneten Daten im Terminal ausgegeben. Leitet man die Terminalausgabe in eine Datei 'Achterbahn.dat' um und liest sie in das Jupyter Notebook 'Achterbahn.ipynb' (View Notebook, Download Notebook) ein, so kann man die numerische Lösung des C++ Programms mit den Python Simulationen vergleichen. Die unteren Abbildungen wurden mittels dieses Notebooks generiert und sie stellen die numerische Python Lösung des grünen Wagens der Animation (blaue Kurve $x(t)$ und rote Kurve $\dot{x}(t)$) im Vergleich zu den Ergebnissen des C++ Programmes dar ($N=10000$, linke Abbildung und $N=100000$, rechte Abbildung). Die untere linke Abbildung zeigt, dass sich die Ergebnisse des C++ Programms ab $t \approx 2$ merklich von der Python Simulation unterscheidet, wohingegen bei einer Simulation mit $N=100000$ Gitterpunkten die Ergebnisse gut miteinander übereinstimmen (rechte Abbildung).
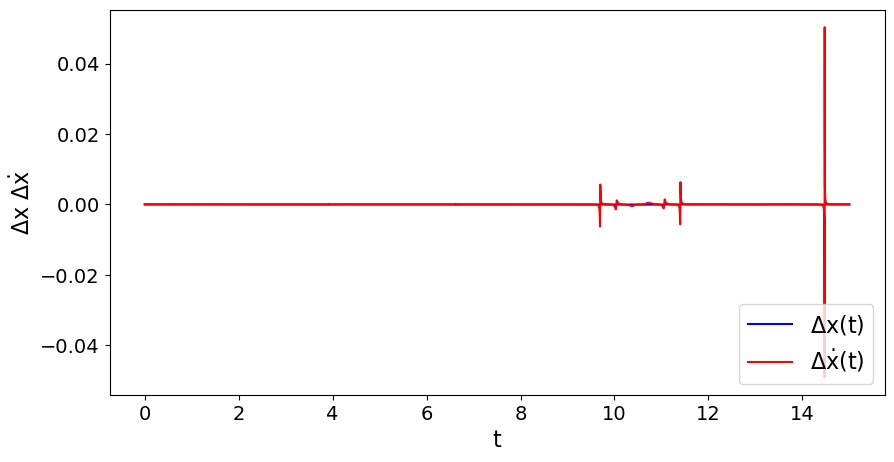
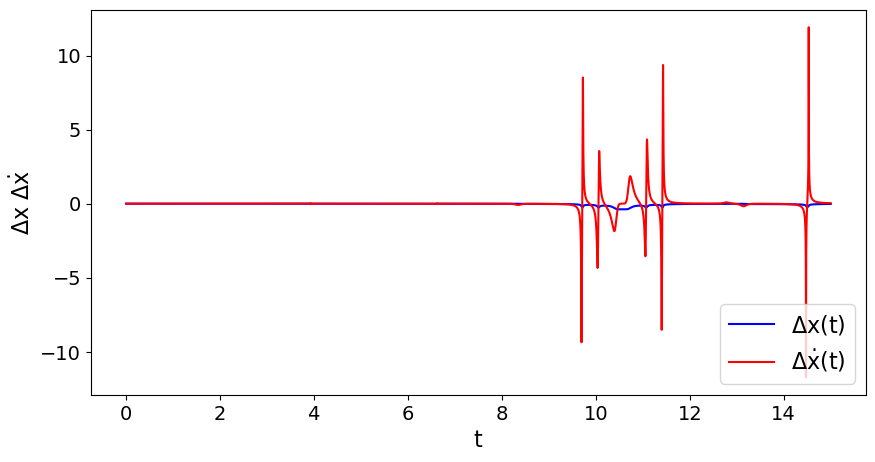
Stellt man jedoch den absoluten Fehler der zeitlichen Verläufe der berechneten Größen dar ($\Delta x$ und $\Delta \dot{x}$), so erkennt man, dass sich auch bei $N=100000$ Gitterpunkten in einigen Bereichen noch große Abweichungen zwischen den Ergebnissen des C++ Programms und der Python Simulation ergeben (rechte untere Abbildung). Erhöht man die Anzahl an zeitlichen Gitterpunkten auf $N=500000$, so verkleinern sich auch diese Abweichungen (linke untere Abbildung). Die C++ und Python Simulationen konvergieren somit für große $N$ zu einer übereinstimmenden zeitlichen Entwicklung des Achterbahn-Wagens.