Das Paradigma der parallelen Programmierung und das Rechnen auf Supercomputern
Einführung
In diesem Unterpunkt werden wir uns mit dem Paradigma der parallelen Programmierung befassen. In diesem Programmierparadigma wird bei der Konzeption von rechenintensiven Computerprogrammen berücksichtigt, dass die Rechenleistung des Computers stets voll ausgelastet ist und separate, voneinander unabhängige Teilaufgaben (Tasks) innerhalb der Programme möglichst gleichzeitig (parallel) berechnet werden.
- "Shared Memory" Mehrprozessorsysteme:
Mehrere Prozessoren eines Computers teilen sich einen gemeinsamen Arbeitsspeicher (RAM). Parallelisierung mittels OpenMP (Open Multi-Processing) relativ einfach möglich. - "Distributed Memory" Mehrprozessorsysteme:
Bei Hochleistungs-Großrechenanlagen sind mehrere Mehrprozessor-Computer zu Computer-Clustern verbunden, wobei jeder Computer seinen eigenen privaten Arbeitsspeicher hat. Parallelisierung mittels MPI (Message Passing Interface).
Die Art und Weise wie ein paralleles Programm zu konzipieren ist, hängt auch von der zugrundeliegenden Rechnerarchitektur des ausführenden Computers ab und man unterscheidet hier grob in die nebenstehenden Varianten. Viele Programmiersprachen lassen sich relativ einfach mittels OpenMP (Open Multi-Processing) parallelisieren, welches sich jedoch nur auf "Shared Memory" Systeme anwenden lässt. MPI (Message Passing Interface) stellt dagegen eine weit verbreitete Parallelisierungsmöglichkeit dar, die sowohl auf "Shared Memory" als auch auf "Distributed Memory" Systemen anwendbar ist. Die Parallelisierung eines sequentiellen Programms mittels MPI ist jedoch ein wenig aufwendiger. Dieser Unterpunkt gibt eine Einführung in die parallele Programmierung mit C++ und OpenMP. Die Parallelisierung eines Python-Programms ist aber natürlich auch möglich und kann z.B. mittels des Python-Moduls (threading oder multiprocessing) implementiert werden, bzw. unter Zuhilfenahme von MPI for Python realisiert werden.
Parallelen Programmierung mit OpenMP
Die parallele Erweiterung eines sequentiellen C++ Programms (ein Programm ohne Parallelisierung) ist mittels OpenMP relativ einfach möglich. Betrachten wir z.B. das folgende C++ Programm, welches für neun unterschiedliche q-Werte den Wert der unendlich geometrischen Reihe berechnet (siehe Übungsblatt Nr. 3, Aufgabe 1). Um die Berechnung möglichst genau zu machen, wurde hierbei ein sehr hoher Wert (50 Millionen) als Obergrenze der Partialsumme benutzt \[ \begin{equation} \sum_{k=0}^{50000000} q^k \, \approx \, \sum_{k=0}^\infty q^k = \frac{1}{1-q},\quad \hbox{mit:} \quad q \in ℝ \,\, , \,\, \left| q \right| < 1 \quad . \end{equation} \]
/* Konvergenzverhalten der geometrischen Reihe für unterschiedliche q * Sequentielle Version der Berechnung von 9 approximierten Werten */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) using namespace std; // Benutze den Namensraum std int main(){ // Hauptfunktion int startTime = time(NULL); // Starten der Zeitmessung double q; // Deklaration des Parameters q long N = 50000000; // Definition der Anzahl der mitgenommenen Summenglieder double wert_approx; // Deklaration des approximierten Wertes der Summe for(int i=1; i <= 9; ++i){ // Schleife zur ueber neun q-Werte q = i*0.1; // Festlegung des q-Wertes wert_approx = 0; // Summenvariable auf Null setzen for(long k=0; k<=N; ++k){ // Schleife zur Berechnung der Summe wert_approx = wert_approx + pow(q,k); // Innerer Teil der geometrischen Reihe } // Ende der Schleife der Summenberechnung printf("q=%6.4f , Wert der Summe = ",q); // Terminalausgabe der berechneten Werte printf("%13.10f (Fehler zum wirklichen Wert : %13.6e ) \n",wert_approx, wert_approx - 1.0/(1-q)); } // Ende der for-Schleife ueber die unterschiedlichen q-Werte // Terminalausgabe der benoetigten Zeit cout << "Das Programm benoetigte: " << time(NULL)-startTime << " Sekunden." << endl; } // Ende Hauptfunktion
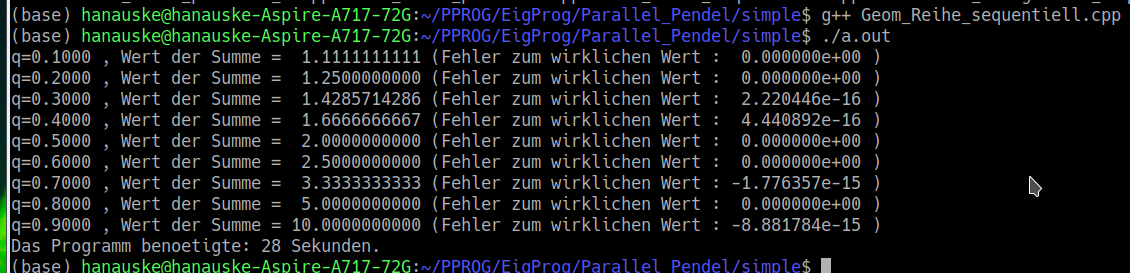
Das Programm berechnet nacheinander, in sequentieller Weise die Werte der geometrischen Reihe für neun unterschiedliche q-Werte und gibt die berechneten Werte im Terminal aus. Zusätzlich wurde eine Zeitmessung der benötigten Rechenzeit im Programm implementiert, die am Ende des Programms ebenfalls ausgegeben wird. Die nebenstehende Abbildung zeigt die Terminalausgabe des Programms. Die berechneten Werte stimmen sehr gut mit den wirklichen Werten der unendlich geometrischen Reihe überein, wobei das Programm jedoch zur Berechnung der neun Werte 28 Sekunden benötigt.
Die parallele Erweiterung dieser sequentiellen Version des Programms ist mittels OpenMP relativ einfach möglich. Da die Berechnung der einzelnen Werte nicht voneinander abhängt und somit die neun unterschiedlichen Berechnungen neun unabhängige 'Tasks' darstellen, kann man die for-Schleife, die die Berechnung der einzelnen Werte durchführt, parallel ausführen. Das folgende C++ Programm stellt diese parallele Version dar:
/* Konvergenzverhalten der geometrischen Reihe für unterschiedliche q * Parallele Version der Berechnung von 9 approximierten Werten * Parallelisierung in der for-Schleife ueber neun q-Werte */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <omp.h> // OpenMP zum parallelen Rechnen using namespace std; // Benutze den Namensraum std int main(){ // Hauptfunktion int startTime = time(NULL); // Starten der Zeitmessung double q; // Deklaration des Parameters q long N = 50000000; // Definition der Anzahl der mitgenommenen Summenglieder double wert_approx; // Deklaration des approximierten Wertes der Summe #pragma omp parallel for private(q,wert_approx) for(int i=1; i <= 9; ++i){ // Schleife zur ueber neun q-Werte q = i*0.1; // Festlegung des q-Wertes wert_approx = 0; // Summenvariable auf Null setzen for(long k=0; k<=N; ++k){ // Schleife zur Berechnung der Summe wert_approx = wert_approx + pow(q,k); // Innerer Teil der geometrischen Reihe } // Ende der Schleife der Summenberechnung printf("q=%6.4f , Wert der Summe = ",q); // Terminalausgabe der berechneten Werte printf("%13.10f (Fehler zum wirklichen Wert : %13.6e ) \n",wert_approx, wert_approx - 1.0/(1-q)); } // Ende der for-Schleife ueber die unterschiedlichen q-Werte // Terminalausgabe der benoetigten Zeit cout << "Das Programm benoetigte: " << time(NULL)-startTime << " Sekunden." << endl; } // Ende Hauptfunktion
Um das Programm zu parallelisieren, bindet man zunächst die OpenMP-Header-Datei mittels '#include <omp.h>' ein. Dann schreibt man vor die zu parallelisierende for-Schleife die Zeile '#pragma omp parallel for '. Dies hat den Effekt, dass nun die einzelnen Summenberechnungen mit den unterschiedlichen q-Werten nicht mehr sequentiell nacheinander ausgeführt werden, sondern mehrere sogenannte Threads die Berechnungen simultan, gleichzeitig ausführen. Spezifiziert man die Anzahl der Threads nicht explizit (mittels omp_set_num_threads()), so entscheidet OpenMP selbständig, in Abhängigkeit von der auf dem Computer zu Verfügung stehenden Prozessor-Kernen, wie viele Threads erzeugt werden sollen. Bei der hier vorliegenden for-Schleife ist bei der Parallelisierung noch das folgende zu beachten: Da die Variablen 'q' und 'wert_approx' von allen Threads benutzt werden, ist es erforderlich diese Variablen beim Parallelisierungsmechanismus als 'private' Thread-Variablen zu kennzeichnen (private(q,wert_approx)), da sie sonst die berechneten Größen der anderen Threads überschreiben. Bemerkung: Man hätte dies auch vermeiden können, falls man die beiden Variablen lokal innerhalb der for-Schleife deklariert hätte.
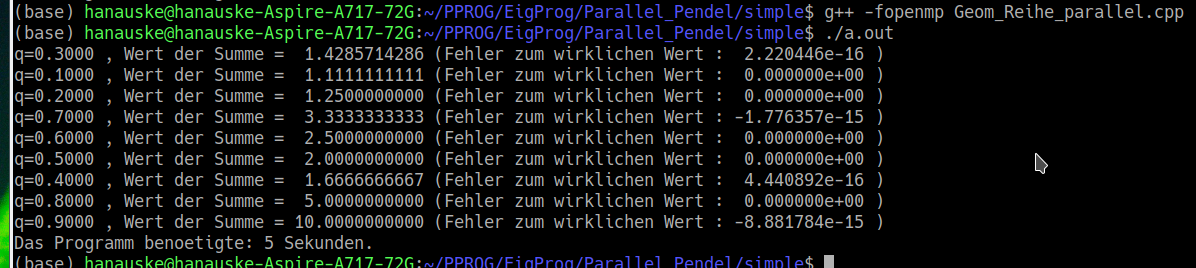
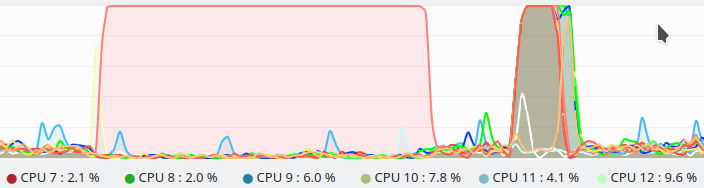
Um ein OpenMP-Programm auch parallel ausführen zu können, muss man es mittels des Zusatzes '-fopenmp' kompilieren ( g++ -fopenmp Geom_Reihe_parallel.cpp ). Die nebenstehende Terminalausgabe zeigt, dass das Programm (auf meinem Laptop) nur 5 Sekunden benötigt. Des Weiteren erkennt man, dass sich die Reihenfolge der ausgegebenen Werte, im Vergleich zum sequentiellen Programm, geändert hat. Die Ausgabe erfolgt nun nicht mehr in Reihenfolge, sondern jeder Thread gibt nach Beendigung seines Tasks den berechneten Wert im Terminal aus. Die nebenstehende Ausgabe zeigt die Auslastung der einzelnen Prozessorkerne (CPUs) meines Laptops beim Ausführen der sequentiellen und parallelen Version des Programms. Beim Ausführen des sequentiellen Programms wird nur ein Prozessorkern benutzt, wohingegen bei der parallelen Version viele der verfügbaren CPUs simultan die einzelnen Werte berechnen und somit viel weniger Zeit benötigt wird (5 Sekunden anstatt 28 Sekunden).
Man hätte die Parallelisierung des Programms auch auf die for-Schleife der Summenberechnung anwenden können, wie die folgende Version des parallelen Programms zeigt.
/* Konvergenzverhalten der geometrischen Reihe für unterschiedliche q * Parallele Version der Berechnung von 9 approximierten Werten * Parallelisierung in der for-Schleife zur Berechnung der Summe bei festem q */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <omp.h> // OpenMP zum parallelen Rechnen using namespace std; // Benutze den Namensraum std int main(){ // Hauptfunktion int startTime = time(NULL); // Starten der Zeitmessung double q; // Deklaration des Parameters q long N = 50000000; // Definition der Anzahl der mitgenommenen Summenglieder double wert_approx; // Deklaration des approximierten Wertes der Summe for(int i=1; i <= 9; ++i){ // Schleife zur ueber neun q-Werte q = i*0.1; // Festlegung des q-Wertes wert_approx = 0; // Summenvariable auf Null setzen #pragma omp parallel for reduction(+:wert_approx) for(long k=0; k<=N; ++k){ // Schleife zur Berechnung der Summe wert_approx = wert_approx + pow(q,k); // Innerer Teil der geometrischen Reihe } // Ende der Schleife der Summenberechnung printf("q=%6.4f , Wert der Summe = ",q); // Terminalausgabe der berechneten Werte printf("%13.10f (Fehler zum wirklichen Wert : %13.6e ) \n",wert_approx, wert_approx - 1.0/(1-q)); } // Ende der for-Schleife ueber die unterschiedlichen q-Werte // Terminalausgabe der benoetigten Zeit cout << "Das Programm benoetigte: " << time(NULL)-startTime << " Sekunden." << endl; } // Ende Hauptfunktion
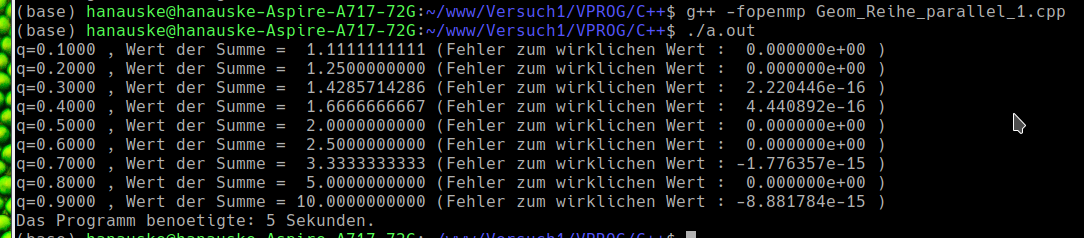
Das Programm benötigt ebenfalls nur 5 Sekunden um die neun Werte zu berechnen und hat zusätzlich den Vorteil, dass die Terminalausgabe in gewohnter Reihenfolge ausgegeben wird. Bei der Parallelisierung ist nun eine Kennzeichnung von privaten Variablen nicht mehr nötig, jedoch ist der Zusatz 'reduction(+:wert_approx)' erforderlich. In der hier gewählten Parallelisierungsvariante werden die einzelnen Teile der Summenberechnung auf mehrere Threads aufgeteilt und es kann dabei ein Schreib-Lese-Konflikt ( race condition ) in der Zeile 'wert_approx = wert_approx + pow(q,k);' auftreten; der Zusatz 'reduction(+:wert_approx)' verhindert diesen Konflikt.
Beispiel: Die parallele OpenMP-Version des C++ Programms "Eine Kiste voller Pendel"
Im Folgenden werden wir eine parallele OpenMP-Version des C++ Programms "Eine Kiste voller Pendel" (siehe Vorlesung 11, Unterpunkt Klausurvorbereitung und prüfungsrelevante Themen) erstellen. Wir benutzen dafür die folgende sequentielle Version des C++ Programms, wobei wir im Vergleich zur ursprünglichen Version zusätzlich eine Zeitmessung eingebaut haben und die Anzahl der Zeitgitterpunkte und das zu simulierende Zeitintervall erhöht haben:
/* Sequentielle Version * 25 Pendel-Simulationen in einem <vector>-Container * Das physikalische und mathematische Pendel mit Reibung (Stokesscher Ansatz) * Berechnung der Lösung einer Differentialgleichung zweiter Ordnung * bzw. eines Systems von zwei Differentialgleichungen erster Ordnung * mittels der Runge-Kutta Ordnung vier Methode * Verfahren zur Loesung der DGL ist in einer abstrakten Basisklasse ausgelagert * Berechnung der Lösung innerhalb einer Methode (Klassenfunktion) Runge-Kutta-Verfahren * Überschreibung der virtuellen Funktion der Bewegungsgleichungen in der abgeleiteten Klasse (Subklasse) Pendel * Zeitentwicklung der fuer unterschiedliche t-Werte in [a,b] * Konstruktor: Pendel(Masse des Pendels, Länge des Pendels l, Reibung beta, Anfangszeit a, Endzeit b, Anzahl der Punkte N, Anfangswerte alpha) * bzw. Konstruktor: Pendel_math(...) * Direkte Ausgabe der berechneten Werte von 25 Pendel-Simulationen in eine Datei (Visualisierung mittels Pendel_Container.py) */ #include "Pendel.hpp" // Header-Datei des physikalischen und mathematischen Pendels mit Reibung (Stokesscher Ansatz) #include <iostream> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <vector> // Sequenzieller Container vector<Type> der Standardbibliothek using namespace std; // Hauptprogramm int main() { int startTime = time(NULL); // Starten der Zeitmessung size_t Anz_Pendel = 25; // Anzahl der zu berechnenden Pendel-Simulationen double m = 1.0; // Masse des Pendels double l = 0.5; // Länge des Pendels double beta = 0; // Reibungskoeffizient double a = 0; // Untergrenze des Zeit-Intervalls double b = 20; // Obergrenze des Intervalls int N = 1000000; // Anzahl der Punkte vector<double> alpha = {0.0,8.2}; // Anfangswerte FILE *ausgabe; // Deklaration eines Files fuer die Ausgabedatei ausgabe = fopen("Pendel_Container.dat", "w+"); // Ergebnisse werden in die Datei "Pendel.dat" geschrieben vector<Pendel> Kiste_Pendel(Anz_Pendel); // Deklaration eines vector-Containers fuer die einzelnen Pendel-Objekte for (size_t n = 0; n < Anz_Pendel; ++n){ // for-Schleife zum Auffuellen des Containers mit Elementen vom Typ 'Pendel' if ((n % 5) == 0) { alpha[1] *= (1 + double(n)/55); beta = 0.0; } // Jeweils 5 Simulationen werden mit gleicher Anfangsgeschwindigkeit gemacht Kiste_Pendel[n] = Pendel(m,l,beta,a,b,N,alpha); // Initialisierung der Pendel-Objekte Kiste_Pendel[n].solve(); // Methode des Runge-Kutta-Verfahrens ausführen beta += 0.2; // Der Parameter beta der Reibung wird veraendert } // Beschreibung der in die Ausgabedatei "Pendel_Container.dat" ausgegebenen Groessen fprintf(ausgabe, "%10s %20s %20s %20s %20s %20s %20s %20s \n", "# Index i", "t-Wert", "x(t), Pendel 1", "y(t), Pendel 1", "v_x(t), Pendel 1", "v_y(t), Pendel 1", "x(t), Pendel 2", "..."); // Ausgabe der Werte for(size_t i=0; i < Kiste_Pendel[0].t.size(); ++i){ // for-Schleife ueber die Zeitgitterpunkte der Simulation if ((i % 500) == 0) { // nur jeden 100-ten Wert ausgeben lassen fprintf(ausgabe, "%10ld %20.12f ",i, Kiste_Pendel[0].t[i]); // Ausgabe des Zeit-Indexes und der aktuellen Zeit in die Ausgabedatei for (auto& n : Kiste_Pendel){ // Bereichsbasierte for-Schleife ueber die einzelnen Pendel-Objekte fprintf(ausgabe, "%20.12f %20.12f %20.12f %20.12f ",n.r(i)[0],n.r(i)[1],n.v(i)[0],n.v(i)[1]); // Ausgabe der Orts- und Geschwindigkeitswerte des Pendel-Objektes } // Ende for-Schleife (Pendel-Objekte) fprintf(ausgabe, "\n"); // Neue Zeile in der Ausgabedatei } // Ende if } // Ende for-Schleife (Zeitgitterpunkte) fclose(ausgabe); // Schliessen der Ausgabedatei cout << "Das Programm benoetigte: " << time(NULL)-startTime << " Sekunden." << endl; // Terminalausgabe der benoetigten Zeit } // Ende Hauptprogramm
Da die einzelnen 25 Pendelsimulationen voneinander unabhängig sind, können wir das Programm in einfacher Weise parallelisieren. Wir lagern dazu die zeitintensive Berechnung der Lösung der Differentialgleichung 'Kiste_Pendel[n].solve();' in eine separate for-Schleife aus, die wir dann parallel ausführen. Das folgende C++ stellt eine parallele Version des Programms dar:
/* parallele Version * 25 Pendel-Simulationen in einem <vector>-Container * Das physikalische und mathematische Pendel mit Reibung (Stokesscher Ansatz) * Berechnung der Lösung einer Differentialgleichung zweiter Ordnung * bzw. eines Systems von zwei Differentialgleichungen erster Ordnung * mittels der Runge-Kutta Ordnung vier Methode * Verfahren zur Loesung der DGL ist in einer abstrakten Basisklasse ausgelagert * Berechnung der Lösung innerhalb einer Methode (Klassenfunktion) Runge-Kutta-Verfahren * Überschreibung der virtuellen Funktion der Bewegungsgleichungen in der abgeleiteten Klasse (Subklasse) Pendel * Zeitentwicklung der fuer unterschiedliche t-Werte in [a,b] * Konstruktor: Pendel(Masse des Pendels, Länge des Pendels l, Reibung beta, Anfangszeit a, Endzeit b, Anzahl der Punkte N, Anfangswerte alpha) * bzw. Konstruktor: Pendel_math(...) * Direkte Ausgabe der berechneten Werte von 25 Pendel-Simulationen in eine Datei (Visualisierung mittels Pendel_Container.py) */ #include "Pendel.hpp" // Header-Datei des physikalischen und mathematischen Pendels mit Reibung (Stokesscher Ansatz) #include <iostream> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <vector> // Sequenzieller Container vector<Type> der Standardbibliothek #include <omp.h> // OpenMP zum parallelen Rechnen using namespace std; // Hauptprogramm int main() { int startTime = time(NULL); // Starten der Zeitmessung size_t Anz_Pendel = 25; // Anzahl der zu berechnenden Pendel-Simulationen double m = 1.0; // Masse des Pendels double l = 0.5; // Länge des Pendels double beta = 0; // Reibungskoeffizient double a = 0; // Untergrenze des Zeit-Intervalls double b = 20; // Obergrenze des Intervalls int N = 1000000; // Anzahl der Punkte vector<double> alpha = {0.0,8.2}; // Anfangswerte FILE *ausgabe; // Deklaration eines Files fuer die Ausgabedatei ausgabe = fopen("Pendel_Container.dat", "w+"); // Ergebnisse werden in die Datei "Pendel.dat" geschrieben vector<Pendel> Kiste_Pendel(Anz_Pendel); // Deklaration eines vector-Containers fuer die einzelnen Pendel-Objekte for (size_t n = 0; n < Anz_Pendel; ++n){ // for-Schleife zum Auffuellen des Containers mit Elementen vom Typ 'Pendel' if ((n % 5) == 0) { alpha[1] *= (1 + double(n)/55); beta = 0.0; } // Jeweils 5 Simulationen werden mit gleicher Anfangsgeschwindigkeit gemacht Kiste_Pendel[n] = Pendel(m,l,beta,a,b,N,alpha); // Initialisierung der Pendel-Objekte beta += 0.2; // Der Parameter beta der Reibung wird veraendert } #pragma omp parallel for // Parallelisierungsanweisung für die folgende, zeitintensive for-Schleife for (size_t n = 0; n < Anz_Pendel; ++n){ // for-Schleife: Parallele Berechnung der Zeitentwicklung der einzelnen Pendel Kiste_Pendel[n].solve(); // Methode des Runge-Kutta-Verfahrens ausführen } // Beschreibung der in die Ausgabedatei "Pendel_Container.dat" ausgegebenen Groessen fprintf(ausgabe, "%10s %20s %20s %20s %20s %20s %20s %20s \n", "# Index i", "t-Wert", "x(t), Pendel 1", "y(t), Pendel 1", "v_x(t), Pendel 1", "v_y(t), Pendel 1", "x(t), Pendel 2", "..."); // Ausgabe der Werte for(size_t i=0; i < Kiste_Pendel[0].t.size(); ++i){ // for-Schleife ueber die Zeitgitterpunkte der Simulation if ((i % 500) == 0) { // nur jeden 100-ten Wert ausgeben lassen fprintf(ausgabe, "%10ld %20.12f ",i, Kiste_Pendel[0].t[i]); // Ausgabe des Zeit-Indexes und der aktuellen Zeit in die Ausgabedatei for (auto& n : Kiste_Pendel){ // Bereichsbasierte for-Schleife ueber die einzelnen Pendel-Objekte fprintf(ausgabe, "%20.12f %20.12f %20.12f %20.12f ",n.r(i)[0],n.r(i)[1],n.v(i)[0],n.v(i)[1]); // Ausgabe der Orts- und Geschwindigkeitswerte des Pendel-Objektes } // Ende for-Schleife (Pendel-Objekte) fprintf(ausgabe, "\n"); // Neue Zeile in der Ausgabedatei } // Ende if } // Ende for-Schleife (Zeitgitterpunkte) fclose(ausgabe); // Schliessen der Ausgabedatei cout << "Das Programm benoetigte: " << time(NULL)-startTime << " Sekunden." << endl; // Terminalausgabe der benoetigten Zeit } // Ende Hauptprogramm

Da die einzelnen Threads immer einem separaten Pendelobjekt zugeordnet sind, ist eine zusätzliche private Kennzeichnung von Variablen nicht nötig und man kann einfach mittels "#pragma omp parallel for" parallelisieren. Die nebenstehende Abbildung zeigt die Terminalausgabe des sequentiellen und parallelen Programms und die unteren Bilder zeigen den zeitlichen Verlauf der Auslastung der Prozessorkerne. Man erkennt eine deutliche Reduzierung der benötigten Zeit.

