Das periodisch angetriebene Pendel
Das periodisch angetriebenes Pendel ist ein Anwendungsfall aus der klassischen Mechanik (siehe z.B. Walter Greiner, 'Klassische Mechanik II' [8. Auflage, 2008, Kapitel VII27. Seite 496]). Das System besteht aus einem Pendel, auf welches zusätzlich eine äußere Kraft mit periodischer Zeitabhängigkeit wirkt. Außerdem soll das Pendel durch eine geschwindigkeitsabhängige Luftreibung gedämpft sein. Die zugrundeliegende Differentialgleichung besitzt die folgende Form \begin{equation} \frac{d^2 \theta(t)}{dt^2} + \frac{\beta}{m} \frac{d \theta(t)}{dt} + \frac{g}{l} \cdot \hbox{sin}\left( \theta(t) \right) = A \cdot \hbox{cos}\left( \Omega \cdot t \right) \quad , \end{equation} wobei $m$ und $l$ die Masse und Länge des Pendels, $\beta$ der Stokessche Reibungskoeffizient und $A$ und $\Omega$ die Amplitude und Frequenz der äußeren Kraft ist. Die zugrundeliegende Bewegungsgleichung des periodisch angetriebenen Pendels ist stark nichtlinear und die, nur auf numerischem Weg zu berechnenden Lösungen, zeigen deterministisch chaotische Bewegungen. Ohne Beschränkung der Allgemeinheit, setzen wir der Einfachheit halber die Masse des Pendels auf $m=1$ und seine Länge auf $l=9.81$, sodass die zugrundeliegende Differentialgleichung des periodisch angetriebenen Pendels die folgende Form besitzt: \begin{equation} \frac{d^2 \theta(t)}{dt^2} + \beta \cdot \frac{d \theta(t)}{dt} + \hbox{sin}\left( \theta(t) \right) = A \cdot \hbox{cos}\left( \Omega \cdot t \right) \end{equation}
Numerische Lösung mit C++ und Python
Wir werden die numerische Lösung der Differentialgleichung sowohl mit Python, als auch mit einem C++ Programm erstellen. In beiden Fällen müssen wir jedoch zunächst die Differentialgleichungen zweiter Ordnung in ein System von zwei Differentialgleichungen erster Ordnung überführen. Näheres zum numerischen Lösen von Differentialgleichungen finden Sie in der Vorlesung Einführung in die Programmierung für Studierende der Physik (Sommersemester 2025), speziell in Vorlesung 9 Systeme von gekoppelten Differentialgleichungen und Differentialgleichungen zweiter Ordnung und in dem Jupyter Notebook Systeme von gekoppelten Differentialgleichungen und Differentialgleichungen zweiter Ordnung.
Umschreiben der Bewegungsgleichung in ein System von Differentialgleichungen erster Ordnung
Wir schreiben nun die obere Bewegungsgleichung zweiter Ordnung in ein System von zwei miteinander gekoppelten Differentialgleichungen erster Ordnung um. Wir machen dafür die vorgegebene Variablenumbenennung ($u_1(t)=\theta(t)$ , $u_2(t)=\dot{\theta}(t) = \frac{d \theta(t)}{dt}$) und definieren das System von DGLs wie folgt: $$ \begin{eqnarray} \dot{u}_1(t) &=& \frac{d u_1}{dt} = \frac{d \theta(t)}{dt} = u_2(t) \\ \dot{u}_2(t) &=& \frac{d u_2}{dt} = \frac{d \dot{\theta}}{dt} = \frac{d^2 \theta(t)}{dt^2} = - \beta \cdot u_2(t) - \hbox{sin}\left( u_1(t) \right) + A \cdot \hbox{cos}\left( \Omega \cdot t \right) := f(t,u_1,u_2) \end{eqnarray} $$
In dem Jupyter Notebook Das periodisch angetriebene Pendel (AngetriebenesPendel.ipynb) benutzen wir zum Lösen des gekoppelten Systems von Differentialgleichungen das Python-Modul SciPy, welches eine breite Kollektion von mathematischen Algorithmen und Funktionen bereitstellt. Im Speziellen werden wir die Funktion 'solve_ivp(...)' verwenden, die sich im Untermodul 'scipy.integrate' befindet, welches Funktionen zum Lösen von gewöhnlichen Differentialgleichungen bereitstellt.
Das C++ Programm
Wir möchten nun das obere System von zwei gekoppelten Differentialgleichungen mit einem C++ Programm numerisch Lösen. Dazu verwenden wir als Vorlage das im Projekt Die schwingende Kette erstellte Programm SchwingendeKette.cpp. In diesem objektorientierten C++ Programm hatten wir den Kern-Algorithmus der numerischen Lösung (Runge-Kutta Ordnung vier Verfahren) in einer C++ Klasse auslagern. Die Klasse 'dsolve' war dabei so allgemein gehalten, das sie die Berechnung der numerischen Lösung für eine beliebige Anzahl von gekoppelten Differentialgleichungen erster Ordnung generieren konnte. In dem folgenden Programm (GetriebenesPendel.cpp) verwenden wir nun diese Klasse zum simulieren der Bewegung des periodisch angetriebenen Pendels.
// Das periodisch angetriebenen Pendel /* ist ein Beispiel eines schwingenden Systems aus dem Bereich der Mechanik * welches bei gewissen Parameterkonstellationen deterministisch chaotische Bewegungen zeigt * Berechnung der Loesung eines Systems von Differentialgleichungen * mittels Runge-Kutta Ordnung vier Verfahren * Verfahren zur Loesung der DGL ist in eine Klasse ausgelagert * Zeitentwicklung der fuer unterschiedliche t-Werte in [a,b] * Konstruktor: dsolve(Anfangszeit a, Endzeit b, Anzahl der Punkte N, Anfangswerte alpha=y(a), DGL als Funktion, Amplitude A der ausseren periodischen Kraft) * Ausgabe zum Plotten mittels Python Jupyter Notebook AngetriebenesPendel.ipynb: "./a.out > GetriebenesPendel.dat */ #include <iostream> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <vector> // Vector-Container der Standardbibliothek #include <functional> // Funktionen in der Argumentenliste von Funktionen using namespace std; // Benutze den Namensraum std class dsolve{ //Definition der Klasse 'dsolve' double a = 0; // Untergrenze des Zeit-Intervalls [a,b] in dem die Loesung berechnet werden soll double b = 1; // Obergrenze des Intervalls [a,b] int N = 10; // Anzahl der Punkte in die das t-Intervall aufgeteilt wird vector<double> alpha {0,0}; // Zwei Anfangswerte (Ort und Geschwindigkeit des Pendels) bei t=a vector<vector<double>> y_RungeK_4; // Deklaration eine double Vektor-Matrix zum speichern der Loesungen vector<double> Zeit; // Deklaration eines double Vektors zum speichern der Zeit-Werte public: // Konstruktor mit sechs Argumenten (Initialisierung der Parameter, Uebergabe der DGL als Funktion, Berechnung der Loesung der DGL) dsolve(double a_, double b_, int N_, vector<double> alpha_, function< vector<double>(double, vector<double>, double)> f, double A) : a(a_),b(b_),N(N_),alpha(alpha_) { double h = (b - a)/N; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) int n = alpha_.size(); // Anzahl der Anfangswerte bzw. DGL-Gleichungen vector<double> k1(n),k2(n),k3(n),k4(n); // Deklaration der vier Runge-Kutta Parameter fuer jede Loesung vector<double> y(n); // Temporaerer Hilfsvektor Zeit.push_back(a_); // Zum Zeit-Vektor die Anfangszeit eintragen y_RungeK_4.push_back(alpha_); // Zum Loesungs-Vektor die Anfangswerte eintragen for(int i=0; i < N; ++i){ // for-Schleife ueber die einzelnen Punkte des t-Intervalls for(int j=0; j < n; ++j){k1[j] = h*f(Zeit[i],y_RungeK_4[i],A)[j];} // for-Schleife ueber die sechs Runge-Kutta k1-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + k1[j]/2;} // Temporaerer Hilfsvektor for(int j=0; j < n; ++j){k2[j] = h*f(Zeit[i]+h/2,y,A)[j];} // for-Schleife ueber die sechs Runge-Kutta k2-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + k2[j]/2;} // Temporaerer Hilfsvektor for(int j=0; j < n; ++j){k3[j] = h*f(Zeit[i]+h/2,y,A)[j];} // for-Schleife ueber die sechs Runge-Kutta k3-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + k3[j];} // Temporaerer Hilfsvektor for(int j=0; j < n; ++j){k4[j] = h*f(Zeit[i]+h,y,A)[j];} // for-Schleife ueber die sechs Runge-Kutta k4-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + (k1[j] + 2*k2[j] + 2*k3[j] + k4[j])/6;} // Temporaerer Hilfsvektor y_RungeK_4.push_back(y); // Zum Loesungs-Vektor den neuen Wert eintragen Zeit.push_back(a + (i+1)*h); // Zum Zeit-Vektor die neue Zeit eintragen } // Ende for-Schleife ueber die einzelnen Punkte des t-Intervalls }; // Ende des Konstruktors const vector<vector<double>>& get_y() const { return y_RungeK_4; } // Definition der konstanten Member-Funktion get_y(), Rueckgabewert Vektor-Matrix der Loesung der DGL const vector<double>& get_zeit() const { return Zeit; } // Definition der konstanten Member-Funktion get_zeit(), Rueckgabewert vector der zeit-Punkte }; // Ende der Klasse // Definition der Bewegungsgleichung des periodisch angetriebenen Pendels vector<double> dgls(double t, vector<double> u_vec, double A){ // mit A der Amplitude der ausseren periodisch Kraft double Omega {2.0/3}; // Frequenz der ausseren periodisch Kraft double beta {0.5}; // Stokessche Reibungskoeffizient vector<double> du_dt; du_dt.push_back(u_vec[1]); // Zwei DGLs erster Ordnung du_dt.push_back(A*cos(Omega*t) - beta*u_vec[1] - sin(u_vec[0])); // eigentliche Bewegungsgleichung return du_dt; // Rueckgabewert der DGLs als Standard-Vektor } // Ende: Definition der Bewegungsgleichung-Funktion // Hauptfunktion int main(){ dsolve Loes {0,300,10000,{0,0},dgls,0.9}; // Benutzt Konstruktor mit a=0, b=300, N=10000, A=0.9 printf("# 0: Index i \n# 1: t-Wert \n# 2: theta \n# 3:d_theta \n"); // Beschreibung der ausgegebenen Groessen for(int i=0; i < Loes.get_zeit().size(); ++i){ // for-Schleife zur Terminalausgabe; Zeitwerte printf("%3d %19.15f %19.15f %19.15f \n",i, Loes.get_zeit()[i], Loes.get_y()[i][0], Loes.get_y()[i][1]); // Ausgabe Index und Zeitwert } // Ende der for-Schleife } // Ende der Hauptfunktion
In dem oben abgebildeten C++ Programm ist die numerische Lösung der Differentialgleichung innerhalb einer Klassenstruktur implementiert, wobei als Klassenname 'dsolve' verwendet wurde. Das zugrundeliegende, zu lösende Differentialgleichungssystem ist in einer vektorwertigen Funktion 'vector<double> dgls(double t, vector<double> u_vec, double A){ ' definiert, die an den Konstruktor der Klasse als Argument übergeben wird. Hier unterscheidet sich das die Klasse dsolve ein wenig von ihrer Vorlage SchwingendeKette.cpp. Da in der Argumentenliste der 'dgls'-Funktion zusätzlich auch der Parameter der Antriebsstärke 'A' aufgelistet wird, wurde die Struktur der Funktion 'f' im Konstruktor der Klasse leicht abgeändert und zusätzlich der Parameter 'A' auch der Argumentenliste des Konstruktors zugefügt. Diese Erweiterung wurde gemacht, damit der Benutzer im Hauptprogramm in einfacher Weise den Parameter 'A' verändern kann. Die Bewegungsgleichung des getriebenen Pendels ist nicht-linear und, abhängig von den Parametern $A$, $\Omega$ und $\beta$ können sehr unterschiedliche und teilweise chaotische Bewegungsformen auftreten.
Numerische Ergebnisse
Im Folgenden werden wir nur einen kleinen Ausschnitt aus dem Parameterraum untersuchen und die Abhängigkeit von der Antriebsstärke $A$ bei festgehaltener Frequenz $\Omega=2/3$ und Reibungskonstante $\beta=0.5$ betrachten.
Kleiner Wert der Antriebsstärke $A=0.9$
Wir beginnen die Diskussion der Ergebnisse und wählen zunächst einen kleinen Wert der Antriebsstärke ($A=0.9$). Dies ist gerade der Wert, den der Benutzer auch im oberen Programm verwendet. Der Konstruktor der Klasse in der Hauptfunktion berechnet die numerische Lösung $\vec{u}(t) = \left( u_1(t), u_2(t) \right)$ einer Simulation im Zeitintervall $t \in [0,300]$ bei vorgegebener Parameterwahl (hier $\beta=0.5$, $\Omega=2/3$ und $A=0.9$). Als Anfangswert zur Zeit $t=0$ betrachten wir das Pendel als ruhend in der Nulllage ($u_1(0) = \theta(0) = \alpha_1 = 0 \,\, , \quad u_2(0) = \dot{\theta}(0) = \alpha_2 = 0$) und wir lösen das Anfangswertproblem unter Verwendung von $N=10000$ zeitlichen Gitterpunkten (mesh points).
Die nebenstehende Animation zeigt die Bewegung des periodisch angetriebenen gedämpften Pendels und die entstehende Phasenraumtrajektorie (Abbildung $\frac{d \theta(t)}{dt}$ vs. $\theta(t)$ bzw. $u_2(t)$ vs. $u_1(t)$) im Zeitbereich von $t \in [0,75]$. Die gepunktete Kurve in der rechten Abbildung zeigt die Phasenraumtrajektorie in der Einschwingphase des Pendels. Man erkennt, dass die Pendelbewegung, nach dieser Einschwingphase, einem Attraktor-Grenzzyklus zuläuft und die Phasenraumtrajektorie dann stabil auf einer periodischen Bewegung bleibt. Bei diesem kleinen Wert der Antriebsstärke ($A=0.9$) vollzieht das Pendel noch keinen Überschlag und es zeigt sich auch noch kein chaotisches Verhalten in seiner Bewegung.
Antriebsstärke $A=1.098$
Wir erhöhen nun die Antriebsstärke der äußeren periodischen Kraft auf $A=1.098$. Die nebenstehende Animation zeigt wieder die Bewegung des Pendels und die zugehörige Phasenraumtrajektorie im Zeitbereich von $t \in [0,75]$. Die Animation zeigt, dass die Bewegung des Pendels auf dem Grenzzyklus einen Überschlag des Pendels periodisch erzeugt, da der Winkel $\theta$ teilweise über $\pi$ ist. Bei solchen Bewegungen werden die Phasenraumtrajektorien gewöhnlich Modulo $2 \pi$ dargestellt. Diese Darstellung wurde auch hier in der rechten Abbildung gewählt. Obwohl das Pendel einen periodischen Überschlag zeigt sieht seine Bewegung nach der Einschwingphase regulär und nicht-chaotisch aus. Dies bestätigt sich auch beim Vergleich der Simulationsergebnisse des C++ Programms mit der numerischen Python Lösung. In dem Jupyter Notebook Das periodisch angetriebene Pendel wurden die Ergebnisse einer Berechnung des C++ Programms mit $N=100000$ Gitterpunkten mit einer Python 'solve_ivp(...)'-Lösung (relative und absolute Fehler-Toleranzen (rtol und atol) von $10^{-13}$) verglichen. Die absoluten Unterschiede beider Lösungen ($\Delta\theta(t) := \theta_{cpp}(t) - \theta_{python}(t)$ und $\Delta\dot{\theta}(t) := \dot{\theta}_{cpp}(t) - \dot{\theta}_{python}(t)$) betrugen dabei lediglich $10^{-10}$ und $10^{-11}$.
Antriebsstärke $A=1.2$
Wir werden sehen, dass nun, bei einer Antriebsstärke von $A=1.2$, chaotische Bewegungsformen auftreten. Die zeitliche Entwicklung von chaotischen Bewegungen ist nicht vorhersagbar und es ist bemerkenswert, dass ein solches Chaos überhaupt in deterministischen Gleichungen entstehen kann (deterministisches Chaos). Aufgrund der hochgradig nicht-linearen Bewegungsgleichung des getriebenen Pendels können sich in gewissen Parameterbereichen kleine Ungenauigkeiten exponentiell vergrößern, sodass eine genaue Vorhersage der Bewegung nach einiger Zeit nicht mehr möglich ist. Die nebenstehende Animation zeigt die Pendelbewegung in diesem chaotischen Bereich. Man erkennt, dass auch nach einer Einschwingphase von $t \in [0,50]$ kein Grenzzyklus der Phasenraumtrajektorie zu erkennen ist und man spricht hierbei von einem chaotischen bzw. seltsamen Attraktor.

Um zu verdeutlichen, dass die Bewegung des Pendels bei einer Antriebsstärke von $A=1.2$ für lange Zeiten nicht genau vorhersagbar ist, vergleichen wir in der nebenstehenden Abbildung mehrere Simulationen miteinander. Die mit Python erstellten Simulationen benutzen zwei unterschiedliche Fehler-Toleranzen (schwarze Kurve $10^{-13}$ und blue Kurve $10^{-10}$) und in einer zusätlichen Simulation wurde der Anfangswert des Pendels zur Zeit $t=0$ nicht exakt in der Nulllage positioniert ist ($\theta_0 = \theta(0) = 10^{-8}$, grüne Kurve). Diese numerischen Lösungen vergleichen wir auch wieder mit den Resultaten des C++ Programms. Bei der Erzeugung der Daten wurden ebenfalls $N=100000$ Gitterpunkte verwndet und bei einer Simulation wurde der Anfangswert des Pendels ebenfalls leicht verschoben (rote gepunktete Kurve). Die Abbildung zeigt, wie sich der Winkel $\theta$ des Pendels im Laufe der Zeit für die unterschiedlichen Simulationen verändert. Man erkennt, dass sich die Simulationen ab einer gewissen Zeit merklich voneinander unterscheiden.
Antriebsstärke $A=1.6$
Erhöht man die Antriebsstärke weiter, auf $A=1.4$, so verschwindet die chaotische Bewegung wieder und man erhält wieder einen Attaktor-Grenzzyklus. Bei weiterer Erhöhung ($A=1.46$ und $A=1.47$) entstehen sogenannte Bifurkation mit Periodenverdopplung und bei $A = 1.5$ ergibt sich dann wieder ein Bereich mit chaotischen Lösungen. Bei einer Antriebsstärke von $A=1.6$ erhält man aber wieder eine reguläre (nicht-chaotische) Lösung (siehe nebenstehende Animation). Die unterschiedlichen numerischen Lösungen gliedern sich somit nach dem Wert der Antriebsstärke $A$, die hier als ein Systemparameter fungiert.
Poincaré-Abbildungen und Attraktordiagramme (Feigenbaum-Diagramme)
Um einen globalen Überblick über das Verhalten eines teils-chaotischen Systems zu erhalten, erstellt man gewöhnlich Poincaré-Abbildungen und Attraktordiagramme. In einem Attraktordiagramm (Feigenbaum-Diagramm) wird die Abfolge von regulären und chaotischen Bereichen visualisiert, indem man den Wert einer der Systemkoordinaten (hier $\dot{\theta}(t_n)$) in regelmäßigen Zeitabständen $t_n$ als Funktion des Systemparameter $A$ darstellt. Das Abtasten der Systemkoordinate geschieht hierbei bei Zeitabständen $t_n$, die durch die charakteristische Frequenz $\Omega$ der äußeren periodischen Kraft definiert sind.
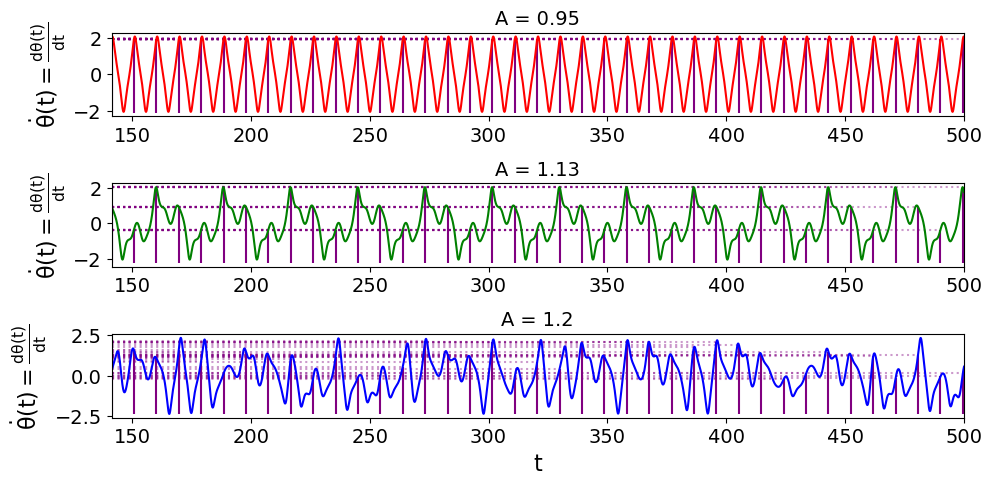
Um diese Vorgehensweise zu verdeutlichen ist die zeitliche Entwicklung der Systemkoordinate für drei Simulationen ($A=0.95$, $A=1.13$ und $A=1.20$) in der nebenstehenden Abbildung dargestellt. Zusätzlich wurden die Werte der Winkelgeschwindigkeiten $\dot{\theta}(t_n)$ bei den Zeitwerten $t_n = t_0 + n \cdot \frac{2 \pi}{\Omega}$ markiert. Die Ergebnisse wurden dabei erst nach einer gewissen Einschwingphase $t_0 = 15 \cdot \frac{2 \pi}{\Omega} \approx 141.37$ visualisiert. Die Abbildung verdeutlicht, dass die Simulationen mit $A=0.95$ und $A=1.13$ eine reguläre Struktur zeigen und als Folge dessen auch die Winkelgeschwindigkeiten $\dot{\theta}(t_n)$ bei den Zeitwerten $t_n$ feste Werte ergeben. Bei $A=0.95$ z.B. einen Wert von $\dot{\theta}(t_n)\approx 1.92$ und für $A=1.13$ drei feste Werte. Hingegen ergeben sich für $A=1.2$ unterschiedliche Werte und es ist keine reguläre Struktur zu erkennen.
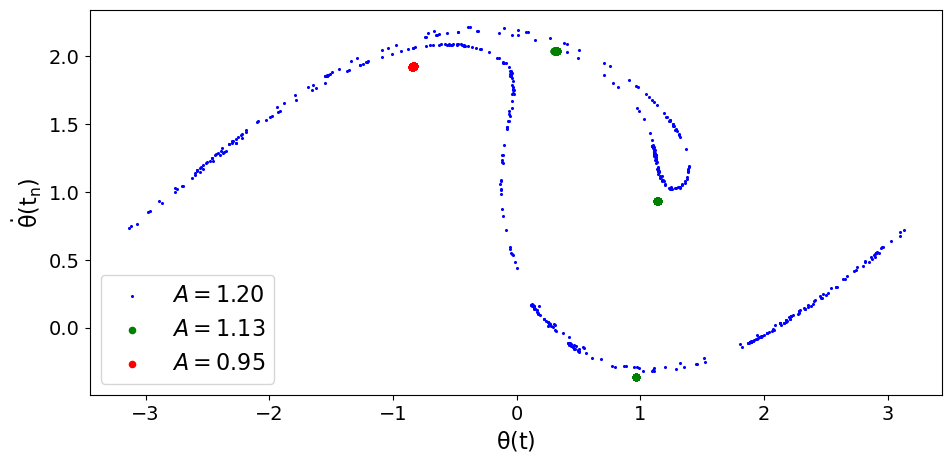
Stellen wir die, bei dieser stroboskopischen Vorgehensweise gewonnenen Werte, in einem $(\theta , \dot{\theta})$-Phasenraum dar, so nennt man diese Abbildung einen Poincaré-Schnitt (Poincaré-Abbildung), und die kontinuierlichen Trajektorien der Simulationen verwandelt sich in eine Punkt-Abbildung. Die Poincaré-Schnitte von regulären, nicht-chaotische Bewegungen bestehen lediglich aus einem Punkt (hier die Simulation mit $A=0.95$) bzw. aus mehreren festen Punkten (hier drei Punkte für die Simulation mit $A=1.13$), wobei sich an der Anzahl der Punkte die Periodenlänge der Schwingung ablesen lässt. Bei chaotischen Bewegungen ergibt sich hingegen ein Poincaré-Schnitt, welcher ausgedehnte Teilbereiche des $(\theta , \dot{\theta})$-Phasenraums bedeckt (hier der seltsame Attraktor der Simulation mit $A=1.2$). Die Poincaré-Schnitte der drei Simulationen sind in der linken unteren Abbildung dargestellt.
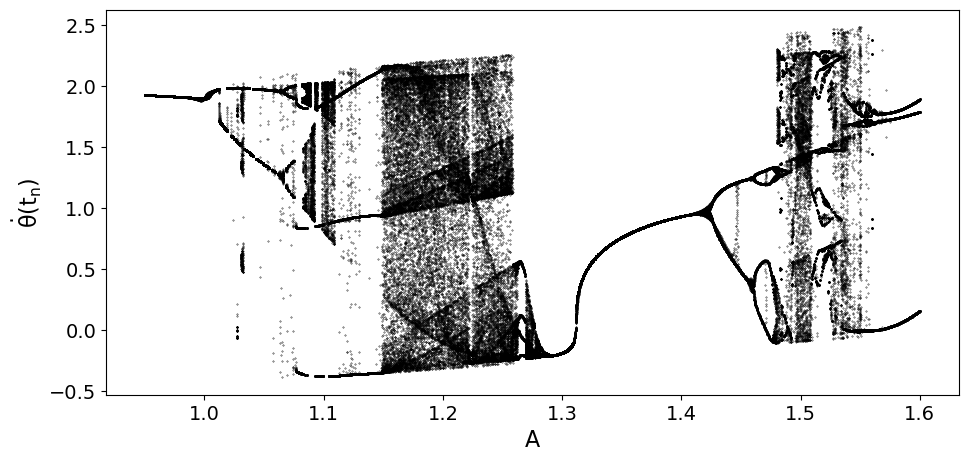
Die Abbildung oben rechts zeigt das sogenannte Attraktordiagramm des periodisch angetriebenen Pendels mit Reibung. Es stellt die Resultaten des C++ Programms GetriebenesPendel_attr_dia.cpp dar (siehe auch GetriebenesPendel_attr_dia_omp.cpp für eine Version mit OpenMP-Parallelisierung). In dem Diagramm werden 2000 unterschiedliche Pendelsimulationen dargestellt, wobei der Wert der Amplitude der äußeren periodischen Kraft von $A=0.95$ auf $A=1.6$ erhöht wurde. Wir stellen für jede der Simulationen die Winkelgeschwindigkeiten $\dot{\theta}(t_n)$ bei den Zeitwerten $t_n = t_0 + n \cdot \frac{2 \pi}{\Omega}$ dar, wobei wir wieder erst nach einer gewissen Einschwingphase $t_0 = 15 \cdot \frac{2 \pi}{\Omega} \approx 141.37$ mit dem Abtasten der Werte starten. In der Abbildung erkennt man gut die Trennung zwischen regulären und chaotischen Bereichen. Man erkennt auch, dass der Übergang von einem regulären Bereich hin zu einem chaotischen Bereich oft mit einer zunächst auftretenden Periodenverdopplung (Bifurkation) verbunden ist.
Im folgenden wird das entsprechende C++ Programm GetriebenesPendel_attr_dia.cpp vorgestellt.
// Das periodisch angetriebenen Pendel /* Beispiel eines schwingenden Systems aus dem Bereich der Mechanik * welches bei gewissen Parameterkonstellationen deterministisch chaotische Bewegungen zeigt * Berechnung der Loesung eines Systems von Differentialgleichungen * mittels Runge-Kutta Ordnung vier Verfahren * Verfahren zur Loesung der DGL ist in einer Klasse ausgelagert * Zeitentwicklung, t-Werte in [a,b] * Konstruktor: dsolve(Anfangszeit a, Endzeit b, Anzahl der Punkte N, Anfangswerte alpha=y(a), DGL als Funktion, Amplitude A, Frequenz Omega der ausseren periodischen Kraft) * Attraktordiagramm vieler Pendel mit unterschiedlichen Amplitudenwerten (Feigenbaumdiagramm) * Ausgabe zum Plotten mittels Python Jupyter Notebook AngetriebenesPendel.ipynb: "./a.out > GetriebenesPendel_attr_dia.dat" */ #include <iostream> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <vector> // Vector-Container der Standardbibliothek #include <functional> // Funktionen in der Argumentenliste von Funktionen using namespace std; // Benutze den Namensraum std // Klasse zum Loesen der DGL des periodisch angetriebenen Pendels class dsolve{ //Definition der Klasse 'dsolve' double a = 0; // Untergrenze des Zeit-Intervalls [a,b] in dem die Loesung berechnet werden soll double b = 1; // Obergrenze des Intervalls [a,b] int N = 10; // Anzahl der Punkte in die das t-Intervall aufgeteilt wird vector<double> alpha = {0,0}; // Zwei Anfangswerte (Ort und Geschwindigkeit des Pendels) bei t=a vector<vector<double>> y_RungeK_4; // Deklaration eine double Vektor-Matrix zum speichern der Loesungen vector<double> Zeit; // Deklaration eines double Vektors zum speichern der Zeit-Werte public: // Konstruktor mit sechs Argumenten (Initialisierung der Parameter, Uebergabe der DGL als Funktion, Berechnung der Loesung der DGL) dsolve(double a_, double b_, unsigned int N_, vector<double> alpha_, function< vector<double>(double, vector<double>, double, double)> f, double A, double Omega) : a(a_),b(b_),N(N_),alpha(alpha_) { double h = (b - a)/N; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) int n = alpha_.size(); // Anzahl der Anfangswerte bzw. DGL-Gleichungen vector<double> k1(n),k2(n),k3(n),k4(n); // Deklaration der vier Runge-Kutta Parameter fuer jede Loesung vector<double> y(n); // Temporaerer Hilfsvektor Zeit.push_back(a_); // Zum Zeit-Vektor die Anfangszeit eintragen y_RungeK_4.push_back(alpha_); // Zum Loesungs-Vektor die Anfangswerte eintragen for(int i=0; i < N; ++i){ // for-Schleife ueber die einzelnen Punkte des t-Intervalls for(int j=0; j < n; ++j){k1[j] = h*f(Zeit[i],y_RungeK_4[i],A,Omega)[j];} // for-Schleife ueber die sechs Runge-Kutta k1-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + k1[j]/2;} // Temporaerer Hilfsvektor for(int j=0; j < n; ++j){k2[j] = h*f(Zeit[i]+h/2,y,A,Omega)[j];} // for-Schleife ueber die sechs Runge-Kutta k2-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + k2[j]/2;} // Temporaerer Hilfsvektor for(int j=0; j < n; ++j){k3[j] = h*f(Zeit[i]+h/2,y,A,Omega)[j];} // for-Schleife ueber die sechs Runge-Kutta k3-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + k3[j];} // Temporaerer Hilfsvektor for(int j=0; j < n; ++j){k4[j] = h*f(Zeit[i]+h,y,A,Omega)[j];} // for-Schleife ueber die sechs Runge-Kutta k4-Parameter for(int j=0; j < n; ++j){y[j] = y_RungeK_4[i][j] + (k1[j] + 2*k2[j] + 2*k3[j] + k4[j])/6;} // Temporaerer Hilfsvektor y_RungeK_4.push_back(y); // Zum Loesungs-Vektor den neuen Wert eintragen Zeit.push_back(a + (i+1)*h); // Zum Zeit-Vektor die neue Zeit eintragen } // Ende for-Schleife ueber die einzelnen Punkte des t-Intervalls }; // Ende des Konstruktors const vector<vector<double>>& get_y() const { return y_RungeK_4; } // Definition der konstanten Member-Funktion get_y(), Rueckgabewert Vektor-Matrix der Loesung der DGL const vector<double>& get_zeit() const { return Zeit; } // Definition der konstanten Member-Funktion get_zeit(), Rueckgabewert vector der zeit-Punkte }; // Ende der Klasse // Definition der Bewegungsgleichung des periodisch angetriebenen Pendels vector<double> dgls(double t, vector<double> u_vec, double A, double Omega){ // A der Amplitude und Omega Frequenz der ausseren periodisch Kraft double beta {0.5}; // Stokessche Reibungskoeffizient vector<double> du_dt; du_dt.push_back(u_vec[1]); // Zwei DGLs erster Ordnung du_dt.push_back(A*cos(Omega*t) - beta*u_vec[1] - sin(u_vec[0])); // eigentliche Bewegungsgleichung return du_dt; // Rueckgabewert der DGLs als Standard-Vektor } // Ende: Definition der Bewegungsgleichung-Funktion // Hauptfunktion int main(){ unsigned int Anz_Pendel = 100; // Anzahl der Pendel im Attraktordiagramm double Omega = 2.0/3.0; // Deklaration und Initialisierung der Frequenz Omega der ausseren periodisch Kraft unsigned int Anz_Punkte = 100000; // Anzahl der Punkte in die das t-Intervall aufgeteilt wird unsigned int Anz_Punkte_attr = 80; // Anzahl der Punkte im Attraktordiagramm (minus 50 Punkte fuer die Einschwingphase) double t_end = Anz_Punkte_attr * 2.0*M_PI/Omega; // Obergrenze des t-Intervalls [0,t_end] als Vielfaches der Zeitabstaende t_ni = 2*M_PI/Omega int i_schritt = Anz_Punkte/Anz_Punkte_attr; // Anzahl der Iterationen fuer einen Zeitabstand t_ni = 2*M_PI/Omega double Anf_A = 0.95; // Anfangswert der Amplitude A der ausseren periodischen Kraft im Attraktordiagramm double End_A = 1.35; // Endwert der Amplitude A der ausseren periodischen Kraft im Attraktordiagramm double dA = (End_A - Anf_A)/(Anz_Pendel-1); // Schrittweite dA der Amplitude A der ausseren periodischen Kraft im Attraktordiagramm vector<vector<double>> attr_wert(Anz_Pendel); // Deklaration einer double Vektor-Matrix zum speichern der Loesungen der Attraktorwerte der unterschiedlichen Pendel // for-Schleife zum Auffuellen des Containers mit unterschiedlichen Pendel-Loesungen for (unsigned int n = 0; n < Anz_Pendel; ++n){ // Pendel-Konstruktor (Zeit-Intervall: [0,t_end], Anzahl der Zeit-Punkte: Anz_Punkte, Anfangsort und Geschwindigkeit: {0,0}, Amplitude A und Frequenz Omega der ausseren periodischen Kraft) dsolve Loes {0,t_end,Anz_Punkte,{0,0},dgls,Anf_A+n*dA,Omega}; // Berechnung der Werte fuer das Attraktordiagramm (Winkelgeschwindigkeit in regelmaessigen Zeitabstaenden t_ni = ni * 2*M_PI/Omega) unsigned int ni = 50; // Deklaration des Integerwertes der Zeitwerte des Attraktordiagramms mit Einschwingphase (50 * 2*M_PI/Omega) vector<double> attr_wert_n; // Deklaration eines vector-Containers der Winkelgeschw. der Pendel-Loesungen zur Zeit t_ni attr_wert_n.push_back(Anf_A+n*dA); // attr_wert_n[0] ist jedoch die Amplitude A der ausseren periodischen Kraft while(ni <= Anz_Punkte_attr){ // while-Schleife ueber alle Zeitwerte des Attraktordiagramms attr_wert_n.push_back( Loes.get_y()[ni*i_schritt][1] ); // Winkelgeschw. zur Zeit t_ni ni++; // Naechster Zeitwert des Attraktordiagramms } // Ende while-Schleife attr_wert[n] = attr_wert_n; // Fuellen der Vektor-Matrix der Attraktordiagramm-Werte des n-ten Pendels } // Ende der for-Schleife, Ende der Parallelisierung for(int n=0; n < Anz_Pendel; ++n){ // for-Schleife zur Terminalausgabe, unterschiedliche Pendel-Loesungen for(int i=0; i < attr_wert[n].size(); ++i){ // for-Schleife zur Terminalausgabe, unterschiedliche Pendel-Zeitwerte t_ni printf("%19.15f ",attr_wert[n][i]); // Ausgabe Winkelgeschw. des n-ten Pendels zur Zeit t_ni } // Ende for-Schleife, Pendel-Zeitwerte t_ni printf("\n"); } // Ende for-Schleife, unterschiedliche Pendel-Loesungen } // Ende der Hauptfunktion
In der Hauptfunktion des Programms werden unter Anderem die Anzahl der Pendelsimulationen, der Anfangs- und Endwert der Amplitude $A$ und die Dauer einer jeden Simulation festgelegt. Damit ein Abtasten der $t_n$-Werte ($t_n = t_0 + n \cdot \frac{2 \pi}{\Omega}$) einfacher wird, wurde die Dauer der Simulation auf ein Vielfaches von $\frac{2 \pi}{\Omega}$ gesetzt. Innerhalb einer for-Schleife werden die Pendelsimulationen mit unterschiedlichen $A$-Werten erzeugt und die Werte der entsprechenden Attraktorwerte der Winkelgeschwindigkeiten $\dot{\theta}(t_n)$ in der Vektor-Matrix 'vector<vector<double>> attr_wert(Anz_Pendel);' gespeichert.
In dem Attraktordiagramm ist es durch eine Farbgebung der Punkte auch möglich Informationen über den Wert der Winkelkoordinate zu erzeugen. In dem unteren Diagramm wurde dafür das C++ Programm leicht abgeändert und neben den Werten $\dot{\theta}(t_n)$ auch die entsprechenden Werte der Winkelkoordinate $\theta(t_n)$ berechnet und gespeichert (siehe GetriebenesPendel_attr_dia_omp_a.cpp). In der unteren Abbildung wurde dann die Farbgebung entsprechend der Winkelkoordinate $\theta(t_n)$ gewählt ($-\pi < \theta \leq \pi$).
