Musterlösung: Projekt Achterbahn
1. Teilaufgabe
Berechnen Sie zunächst auf analytischem Weg, mittels eines Jupyter Notebooks unter Verwendung der SymPy Bibliothek, die Euler-Lagrange Gleichungen der Bewegung eines Wagens auf der Achterbahn, wobei der Verlauf der Metallschiene der Achterbahn durch die Funktion $h(x) = e^{\frac{\sqrt{x^2}}{10}} \cdot \left( \hbox{sin}\left( \frac{x^2}{10} \right) \right)^2$ bestimmt ist. Schreiben Sie dann die Bewegungsgleichung in ein System von erster Ordnung Differentialgleichungen um.
Das nebenstehende Python Jupyter Notebook 'Achterbahn_2.ipynb' (View Notebook, Download Notebook) stellt eine Musterlösung der ersten Teilaufgaben des Projektes Die Achterbahn dar.
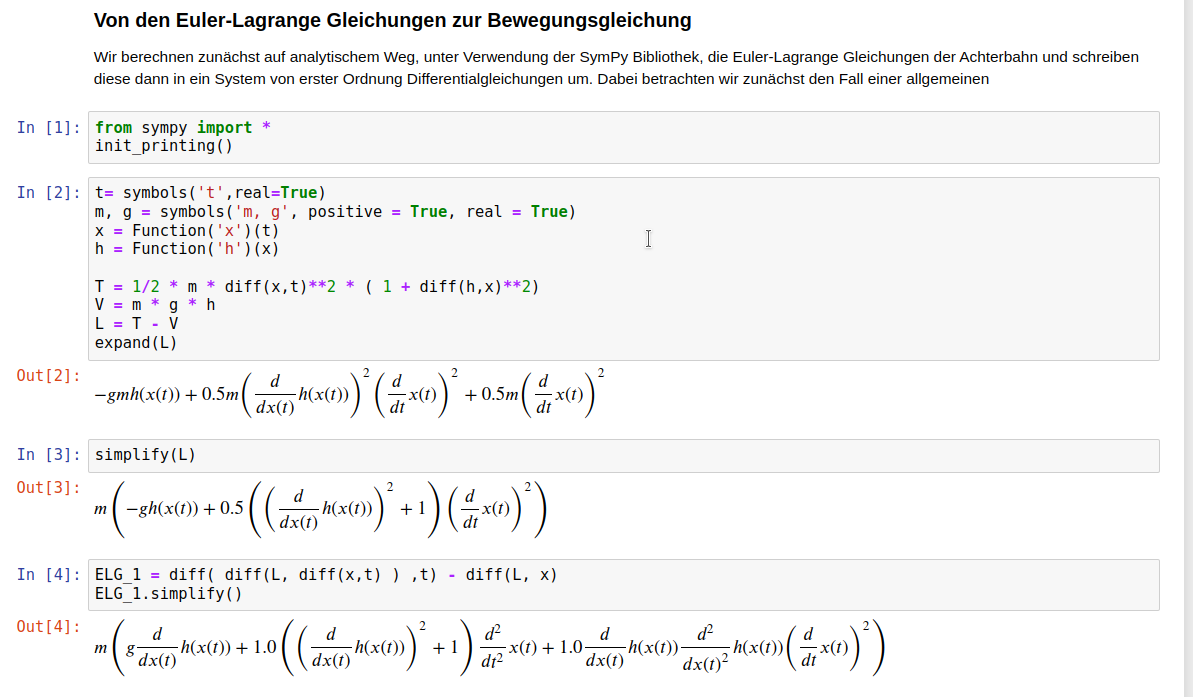
Wir berechnen zunächst auf analytischem Weg, unter Verwendung der SymPy Bibliothek, die Euler-Lagrange Gleichungen der Achterbahn und schreiben diese dann in ein System von erster Ordnung Differentialgleichungen um. Dabei betrachten wir zunächst den Fall einer allgemeinen Funktion $h(x)$, damit eine, in späteren Teilaufgaben möglicherweise abgeänderte Form der Achterbahn, einfach in den Algorithmus eingebaut werden kann. Wir definieren zunächst die nötigen SymPy-Symbole und SymPy-Funktionen und implementieren die Lagrangefunktion $L = T - V$ in der folgenden Form: $$ \begin{eqnarray} &T = \frac{1}{2} m \left[ \dot{x}(t)^2 + \dot{y}(t)^2 \right] = \frac{1}{2} m \, \dot{x}^2 \cdot \left[ 1 + \left( \frac{d h(x)}{dx} \right)^2 \right] &\\ &V(t) = m \, g \cdot y(t) = m \, g \cdot h(x(t)) & \end{eqnarray} $$ Mittels der Euler-Lagrange Gleichungen $$ \begin{equation} \frac{d }{dt} \left( \frac{\partial L}{\partial \dot{x}} \right) - \frac{\partial L}{\partial x} \, =\, 0 \end{equation} $$ erhält man die folgende Bewegungsgleichungen (siehe auch unterste Gleichung in der nebenstehenden Abbildung) $$ \begin{equation} m \left(g \frac{d}{d x{\left (t \right )}} h{\left (x{\left (t \right )} \right )} + \left(\left(\frac{d}{d x{\left (t \right )}} h{\left (x{\left (t \right )} \right )}\right)^{2} + 1\right) \frac{d^{2}}{d t^{2}} x{\left (t \right )} + \frac{d}{d x{\left (t \right )}} h{\left (x{\left (t \right )} \right )} \frac{d^{2}}{d x{\left (t \right )}^{2}} h{\left (x{\left (t \right )} \right )} \left(\frac{d}{d t} x{\left (t \right )}\right)^{2}\right) \, =\, 0 \quad . \end{equation} $$ Die Bewegung des Wagens wird somit durch eine Differentialgleichung zweiter Ordnung bestimmt und diese hängt nicht von dem Wert der Masse des Wagens ab. Wir formen die DGL in die übliche Form einer Differentialgleichung zweiter Ordnung um: $$ \begin{equation} \ddot{x}(t) = \frac{d^{2}}{d t^{2}} x{\left (t \right )} = - \frac{\left(g + \frac{d^{2}}{d x^{2}} h{\left (x \right )} \left(\frac{d}{d t} x{\left (t \right )} \right)^{2}\right) \frac{d}{d x } h{\left (x \right )}}{\left(\frac{d}{d x } h{\left (x \right )}\right)^{2} + 1} = f(t,x,\dot{x}) \end{equation} $$
Setzt man nun die formbestimmende Funktion $h(x) = e^{\frac{\sqrt{x^2}}{10}} \cdot \left( \hbox{sin}\left( \frac{x^2}{10} \right) \right)^2$ ein, so erhält man mittels Sympy den in der folgenden Abbildung dargestellte Ausdruck für die DGL bestimmende Funktion $f(t,x,\dot{x})$.

Die obige Ausgabe verwendeten wir dann schließlich für im C++ Programm Achterbahn_1.cpp und Achterbahn_2.cpp.
Um die entstandene DGL zweiter Ordnung numerisch lösen zu können, schreiben wir sie in ein System von zwei DGLs erster Ordnung um. Wir betrachten nun die numerische Lösung und machen die folgenden Variablenumbenennung: $u_1(t)=x(t)$, und $u_2(t)=\dot{x}(t)$ und definieren das System von DGLs wie folgt: $$ \begin{eqnarray} \dot{u_1}(t) &=& \frac{d u_1}{dt} = \frac{d x}{dt} = u_2(t) \\ \dot{u_2}(t) &=& \frac{d u_2}{dt} = \frac{d \dot{x}}{dt} = \ddot{x}(t) = f(u_1,u_2) = f(t,x,\dot{x}) \end{eqnarray} $$
2. Teilaufgabe
Der Wagen ($m=100$ [Kg]) werde zur Zeit $t=0$ [s], mit einer Anfangsgeschwindigkeit von $\dot{x}(0) = 30.42$ [km/h] bei $x=0.01$ [m] in die Achterbahn katapultiert. Lösen Sie das System von Differentialgleichungen erster Ordnung zunächst mittels Python und visualisieren Sie die Simulation in einem Jupyter Notebook. Erhöhen Sie nun die Anfangsgeschwindigkeit auf $\dot{x}(0) = 60$ [km/h] und stellen beide numerischen Lösungen in einer Animation dar.
Die nebenstehende Animation stellt die Bewegung der beiden Wagen dar und wurde mit dem Python Jupyter Notebook 'Achterbahn_2.ipynb' (View Notebook, Download Notebook) erstellt. Der rote Wagen wurde mit $\dot{x}(0) = 30.42$ [km/h] in die Bahn katapultiert und der grüne Wagen mit $\dot{x}(0) = 60$ [km/h].
3. Teilaufgabe
Lösen Sie nun das System von Differentialgleichungen erster Ordnung mittels eines C++ Programms und benutzen Sie das Runge-Kutta Ordnung vier Verfahren.
Als Vorlage verwenden wir das in der vorigen Vorlesung vorgestellte C++ Programm DGL_2_a.cpp, das eine Differentialgleichung zweiter Ordnung mittels der Euler- und Runge-Kutta Ordnung vier Methode löst (siehe unteres Frame). Die für unser Problem keine analytische Lösung existiert, benötigen wir die Funktionen 'double u_1_analytisch(...)' und 'double u_2_analytisch(...)' nicht mehr. Die DGL bestimmende Funktion $f(t,x,\dot{x})$ exportieren wir uns als C++ Quelltext vom Jupyter Notebook und fügen den Ausdruck in der Funktion 'double f_2(...)' anstelle von 'wert = 2*u_2 - 2*u_1 + exp(2*t)*sin(t);' (es wäre vielleicht an dieser Stelle eleganter gewesen, hätte man den allgemeinen Ausdruck für $f(t,x,\dot{x})$ verwendet, indem die Funktion $h(x)$ noch nicht festgelegt wurde). Da wir unser System nur mit der Runge-Kutta Ordnung vier Methode lösen möchten, benötigen wir die Variablen und Ausdrücke nicht mehr, die das Euler Verfahren betreffen (z.B. 'double u_Euler_1 = alpha_1;' oder 'double tmp;').
/* Berechnung der Lösung einer Differentialgleichung zweiter Ordnung ( y''= 2*y' - 2*y + exp(2*t)*sin(t) ) * welches in ein System von zwei Differentialgleichung umgeschrieben wurde * Form des DGL Systems: u_1'=y'=f_1(t,u_1,u_2)=u_2 , u_2'=y''=f_2(t,u_1,u_2) * Loesung mittels der Euler Methode und Runge-Kutta Ordnung vier Methode * Zeitentwicklung von u_1(t), u_2(t) fuer unterschiedliche t-Werte in [a,b] * Ausgabe zum Plotten mittels Python Jupyter Notebook DGL_2.ipynb: "./a.out >> DGL_2_a.dat */ #include <stdio.h> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) double f_1(double t, double u_1, double u_2){ // Deklaration und Definition der Funktion f_1(t,u_1,u_2) double wert; wert = u_2; // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f_1 } // Ende der Funktion f_1 double f_2(double t, double u_1, double u_2){ // Deklaration und Definition der Funktion f_2(t,u_1,u_2) double wert; wert = 2*u_2 - 2*u_1 + exp(2*t)*sin(t); // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f_2 } // Ende der Funktion f_2 double u_1_analytisch(double t, double alpha_1, double alpha_2){ // Analytische Loesung y(t)=u_1(t) double wert; // bei gegebenem Anfangswert y(a)=1, y'(a)=1 wert = exp(t)*sin(t)*(alpha_2 + 1.0/5.0 - alpha_1) + exp(t)*cos(t)*(alpha_1 + 2.0/5.0) + ((sin(t) - 2*cos(t))*exp(2*t))/5.0; return wert; // Rueckgabewert } // Ende der Definition double u_2_analytisch(double t, double alpha_1, double alpha_2){ // Analytische Loesung y'(t)=u_2(t) double wert; // bei gegebenem Anfangswert y(a)=1, y'(a)=1 wert = ((-3*cos(t) + 4*sin(t))*exp(2*t))/5.0 - 2*((alpha_1 - alpha_2/2.0 + 1.0/10.0)*sin(t) - cos(t)*(alpha_2 + 3.0/5.0)/2.0)*exp(t); return wert; // Rueckgabewert } // Ende der Definition int main(){ // Hauptfunktion double a = 0; // Untergrenze des Zeit-Intervalls [a,b] in dem die Loesung berechnet werden soll double b = 1; // Obergrenze des Intervalls [a,b] int N = 100; // Anzahl der Punkte in die das t-Intervall aufgeteilt wird double h = (b - a)/N; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) double alpha_1 = -0.4; // 1.Anfangswert bei t=a: u_1(a)=alpha_1 double alpha_2 = -0.6; // 2.Anfangswert bei t=a: u_2(a)=alpha_2 double t; // Aktueller Zeitwert double u_Euler_1 = alpha_1; // Deklaration und Initialisierung der numerischen Loesung der Euler Methode fuer u_1 double u_RungeK_4_1 =alpha_1; // Deklaration und Initialisierung der numerischen Loesung der Runge-Kutta Ordnung vier Methode double k1_1,k2_1,k3_1,k4_1; // Deklaration der vier Runge-Kutta Parameter fuer u_1 double u_Euler_2 = alpha_2; // Deklaration und Initialisierung der numerischen Loesung der Euler Methode fuer u_2 double u_RungeK_4_2 = alpha_2; // Deklaration und Initialisierung der numerischen Loesung der Runge-Kutta Ordnung vier Methode double k1_2,k2_2,k3_2,k4_2; // Deklaration der vier Runge-Kutta Parameter fuer u_2 double tmp; // Variable zum Zwischenspeichern von Ergebnissen printf("# 0: Index i \n# 1: t-Wert \n# 2: Euler Methode y=u1 \n# 3: Euler Methode y'=u2 \n# 4: Runge-Kutta Ordnung vier y=u1 \n"); printf("# 5: Runge-Kutta Ordnung vier y'=u2 \n# 6: Analytische Loesung y=u1 \n# 7: Analytische Loesung y'=u2 \n"); // Beschreibung der ausgegebenen Groessen for(int i=0; i <= N; ++i){ // for-Schleife ueber die einzelnen Punkte des t-Intervalls t = a + i*h; // Zeit-Parameter wird um h erhoeht printf("%3d %19.15f %19.15f %19.15f %19.15f %19.15f ",i, t, u_Euler_1, u_Euler_2,u_RungeK_4_1, u_RungeK_4_2); // Ausgaben der Loesungen printf(" %19.15f %19.15f \n",u_1_analytisch(t,alpha_1,alpha_2),u_2_analytisch(t,alpha_1,alpha_2)); // Ausgaben der Loesungen tmp = u_Euler_1 + h*f_1(t,u_Euler_1,u_Euler_2); // Euler Methode u_Euler_2 = u_Euler_2 + h*f_2(t,u_Euler_1,u_Euler_2); // u_2 u_Euler_1 = tmp; // u_1 k1_1 = h*f_1(t,u_RungeK_4_1,u_RungeK_4_2); // Runge-Kutta Parameter k1 fuer u_1 k1_2 = h*f_2(t,u_RungeK_4_1,u_RungeK_4_2); // Runge-Kutta Parameter k1 fuer u_2 k2_1 = h*f_1(t+h/2,u_RungeK_4_1+k1_1/2,u_RungeK_4_2+k1_2/2); // Runge-Kutta Parameter k2 fuer u_1 k2_2 = h*f_2(t+h/2,u_RungeK_4_1+k1_1/2,u_RungeK_4_2+k1_2/2); // Runge-Kutta Parameter k2 fuer u_2 k3_1 = h*f_1(t+h/2,u_RungeK_4_1+k2_1/2,u_RungeK_4_2+k2_2/2); // Runge-Kutta Parameter k3 fuer u_1 k3_2 = h*f_2(t+h/2,u_RungeK_4_1+k2_1/2,u_RungeK_4_2+k2_2/2); // Runge-Kutta Parameter k3 fuer u_2 k4_1 = h*f_1(t+h,u_RungeK_4_1+k3_1,u_RungeK_4_2+k3_2); // Runge-Kutta Parameter k4 fuer u_1 k4_2 = h*f_2(t+h,u_RungeK_4_1+k3_1,u_RungeK_4_2+k3_2); // Runge-Kutta Parameter k4 fuer u_2 u_RungeK_4_1 = u_RungeK_4_1 + (k1_1 + 2*k2_1 + 2*k3_1 + k4_1)/6; // Runge-Kutta Ordnung vier Methode fuer u_1 u_RungeK_4_2 = u_RungeK_4_2 + (k1_2 + 2*k2_2 + 2*k3_2 + k4_2)/6; // Runge-Kutta Ordnung vier Methode fuer u_2 } // Ende for-Schleife ueber die einzelnen Punkte des t-Intervalls } // Ende der Hauptfunktion
Im Hinblick auf die spätere Teilaufgabe, der Konstruktion einer Achterbahn-Klasse, lagern wir schon an dieser Stelle den Teil der numerischen Lösung der DGL in eine Klasse aus. Diese Klasse kann dann später als die Achterbahn-Klasse definiert werden, wobei Sie an dieser Stelle lediglich die Lösung der Bewegungsgleichungen mittels des Runge-Kutta Ordnung vier Verfahrens beinhalten soll. Es wird im Folgenden eine Klassenstruktur verwendet, bei der die Instanzen der Klasse die Bewegungen eines Wagens mit spezifizierten Anfangswerten beschreiben sollen. Mittels des Konstruktors soll der Benutzer der Klasse die Anfangswerte festlegen können und außerdem spezifizieren, in welchem Zeitintervall $[a,b]$ und mit wievielen Zeitgitterpunkte $N$ er die numerische Rechnung durchgeführt haben möchte. Im Hauptprogramm soll dann lediglich der zu simulierende Wagen als Objekt dieser Klasse definiert und die berechneten Werte im Terminal ausgegeben werden.
Da es wohl, im Hinblick auf spätere Teilaufgaben, ein schon recht umfangreiches Programm werden wird, teilen wir die Datei des Quelltextes in zumindest zwei separate Dateien auf (das Aufteilen von großen Programmen in mehrere Unterdateien wird in einer der späteren Vorlesungen genauer behandelt). Das Hauptprogramm und die Definition der DGL bestimmenden Funktion ist in dem folgenden C++ Programm in der Quelldatei Achterbahn_1.cpp zu finden, wobei die Klasse der numerischen Berechnung in eine hpp-Datei (Achterbahn_1.hpp) geschrieben wurde. Die Endung '.hpp' bezeichnet eine besondere Art von Quellcodedatei, eine sogenannte 'Header Datei', die dann im main()-Programm mittels '#include "Achterbahn_1.hpp"' eingebunden wird.
/* Klasse zur Berechnung der Loesung einer Differentialgleichung der Form y''=f_2(t,y) * mittels Runge-Kutta Ordnung vier Verfahren * Verfahren zur Loesung der DGL ist in eine Klasse ausgelagert * Zeitentwicklung der fuer unterschiedliche t-Werte in [a,b] * Kostruktor: Achterbahn_1(Anfangszeit a, Endzeit b, Anzahl der Punkte N, Anfangswert1 alpha_1=y(a)=u_1(a), Anfangswert2 alpha_2=y'(a)=u_2(a),) */ #include <stdio.h> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <vector> // Vector-Container der Standardbibliothek using namespace std; // Benutze den Namensraum std class Achterbahn_1{ //Definition der Klasse 'Achterbahn_1' double a = 0; // Untergrenze des Zeit-Intervalls [a,b] in dem die Loesung berechnet werden soll double b = 1; // Obergrenze des Intervalls [a,b] const unsigned int N = 5000; // Anzahl der Punkte in die das t-Intervall aufgeteilt wird double h = (b - a)/N; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) double alpha_1 = 0.0; // 1.Anfangswert bei t=a: u_1(a)=alpha_1 double alpha_2 = 0.0; // 2.Anfangswert bei t=a: u_2(a)=alpha_2 double t = a; // Aktueller Zeitwert double k1_1,k2_1,k3_1,k4_1; // Deklaration der vier Runge-Kutta Parameter fuer u_1 double k1_2,k2_2,k3_2,k4_2; // Deklaration der vier Runge-Kutta Parameter fuer u_2 vector<double> Zeit; // Deklaration eines double Vektors zum Speichern der Zeit-Werte vector<double> u_RungeK_4_1; // Deklaration eines double Vektors zum Speichern der Loesung fuer u_1 vector<double> u_RungeK_4_2; // Deklaration eines double Vektors zum Speichern der Loesung fuer u_2 public: // Konstruktor mit fuenf Argumenten (Initialisierung der Parameter, Berechnung der Loesung der DGL) Achterbahn_1(double a_, double b_, const unsigned int N_, double alpha_1_, double alpha_2_) : a(a_),b(b_),N(N_),alpha_1(alpha_1_),alpha_2(alpha_2_) { Zeit.resize( N + 1 ); // Die Anzahl der Eintraege im Vektor wird auf N+1 erhoeht u_RungeK_4_1.resize( N + 1 ); // Die Anzahl der Eintraege im Vektor wird auf N+1 erhoeht u_RungeK_4_2.resize( N + 1 ); // Die Anzahl der Eintraege im Vektor wird auf N+1 erhoeht Zeit[ N ] = b; // Zum Zeit-Vektor die Endzeit eintragen u_RungeK_4_1[0] = alpha_1; // Zum y-Vektor den Anfangswert alpha_1=y(a) eintragen u_RungeK_4_2[0] = alpha_2; // Zum y'-Vektor den Anfangswert alpha_2=y'(a) eintragen for(int i=0; i < N; ++i){ // for-Schleife ueber die einzelnen Punkte des t-Intervalls t = a + i*h; // Zeit-Parameter wird um h erhoeht Zeit[i] = t; // Zum Zeit-Vektor die neue Zeit eintragen k1_1 = h*f_1(t,u_RungeK_4_1[i],u_RungeK_4_2[i]); // Runge-Kutta Parameter k1 fuer u_1 k1_2 = h*f_2(t,u_RungeK_4_1[i],u_RungeK_4_2[i]); // Runge-Kutta Parameter k1 fuer u_2 k2_1 = h*f_1(t+h/2,u_RungeK_4_1[i]+k1_1/2,u_RungeK_4_2[i]+k1_2/2); // Runge-Kutta Parameter k2 fuer u_1 k2_2 = h*f_2(t+h/2,u_RungeK_4_1[i]+k1_1/2,u_RungeK_4_2[i]+k1_2/2); // Runge-Kutta Parameter k2 fuer u_2 k3_1 = h*f_1(t+h/2,u_RungeK_4_1[i]+k2_1/2,u_RungeK_4_2[i]+k2_2/2); // Runge-Kutta Parameter k3 fuer u_1 k3_2 = h*f_2(t+h/2,u_RungeK_4_1[i]+k2_1/2,u_RungeK_4_2[i]+k2_2/2); // Runge-Kutta Parameter k3 fuer u_2 k4_1 = h*f_1(t+h,u_RungeK_4_1[i]+k3_1,u_RungeK_4_2[i]+k3_2); // Runge-Kutta Parameter k4 fuer u_1 k4_2 = h*f_2(t+h,u_RungeK_4_1[i]+k3_1,u_RungeK_4_2[i]+k3_2); // Runge-Kutta Parameter k4 fuer u_2 u_RungeK_4_1[i+1] = u_RungeK_4_1[i] + (k1_1 + 2*k2_1 + 2*k3_1 + k4_1)/6; // Zum y-Vektor den neuen Wert eintragen u_RungeK_4_2[i+1] = u_RungeK_4_2[i] + (k1_2 + 2*k2_2 + 2*k3_2 + k4_2)/6; // Zum y'-Vektor den neuen Wert eintragen } // Ende for-Schleife ueber die einzelnen Punkte des t-Intervalls }; // Ende des Konstruktors double f_1(double t, double u_1, double u_2); // Deklaration der Member-Funktion f_1(t,y) (Definition findet ausserhalb der Klasse statt) double f_2(double t, double u_1, double u_2); // Deklaration der Member-Funktion f_2(t,y) (Definition findet ausserhalb der Klasse statt) const vector<double>& get_u_1() const { return u_RungeK_4_1; } // Definition der konstanten Member-Funktion get_u_1, Rueckgabewert vector der Loesung y(t)=u_1(t) der DGL const vector<double>& get_u_2() const { return u_RungeK_4_2; } // Definition der konstanten Member-Funktion get_u_2, Rueckgabewert vector der Loesung y'(t)=u_2(t) der DGL const vector<double>& get_zeit() const { return Zeit; } // Definition der konstanten Member-Funktion get_zeit(), Rueckgabewert vector der zeit-Punkte }; // Ende der Klasse
// Musterlösung Projekt Achterbahn (Aufgabe 1) /* Berechnung der Lösung einer Differentialgleichung der Form x'=f(t,x) * mittels Runge-Kutta Ordnung vier Verfahren * Verfahren zur Loesung der DGL ist in eine Klasse ausgelagert * Zeitentwicklung der fuer unterschiedliche t-Werte in [a,b] */ #include "Achterbahn_1.hpp" // Einbinden der Klasse die das System der DGLs mittels Runge-Kutta Ordnung vier loest #include <stdio.h> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <vector> // Vector-Container der Standardbibliothek using namespace std; // Benutze den Namensraum std double Achterbahn_1::f_1(double t, double u_1, double u_2){ // Deklaration und Definition der Funktion f_1(t,u_1,u_2) double wert; wert = u_2; // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f_1 } // Ende der Funktion f_1 double Achterbahn_1::f_2(double t, double u_1, double u_2){ // Deklaration und Definition der Funktion f_2(t,u_1,u_2), berechnet mittels des Jupyter Notebooks Achterbahn.ipynb double wert; wert = 0.20000000000000001*u_1*(-32.0*pow(u_1, 4)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*pow(cos(0.10000000000000001*pow(u_1, 2)), 3) + 16.0*pow(u_1, 4)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*cos(0.10000000000000001*pow(u_1, 2)) + 75.894663844041105*pow(u_1, 2)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*pow(sin(0.10000000000000001*pow(u_1, 2)), 3)*fabs(u_1) + 80.0*pow(u_1, 2)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*pow(sin(0.10000000000000001*pow(u_1, 2)), 3) - 63.245553203367592*pow(u_1, 2)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*sin(0.10000000000000001*pow(u_1, 2))*fabs(u_1) - 80.0*pow(u_1, 2)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*sin(0.10000000000000001*pow(u_1, 2)) + 60.0*pow(u_1, 2)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*pow(cos(0.10000000000000001*pow(u_1, 2)), 3) - 60.0*pow(u_1, 2)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*cos(0.10000000000000001*pow(u_1, 2)) - 1962.0*pow(u_1, 2)*exp(0.316227766016838*fabs(u_1))*cos(0.10000000000000001*pow(u_1, 2)) - 15.811388300841898*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*pow(sin(0.10000000000000001*pow(u_1, 2)), 3)*fabs(u_1) + 63.245553203367592*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*pow(cos(0.10000000000000001*pow(u_1, 2)), 3)*fabs(u_1) - 63.245553203367592*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*cos(0.10000000000000001*pow(u_1, 2))*fabs(u_1) - 1551.0971923125903*exp(0.316227766016838*fabs(u_1))*sin(0.10000000000000001*pow(u_1, 2))*fabs(u_1))*sin(0.10000000000000001*pow(u_1, 2))/(100.0*pow(u_1, 2) + pow(4.0*pow(u_1, 2)*cos(0.10000000000000001*pow(u_1, 2)) + 3.1622776601683795*sin(0.10000000000000001*pow(u_1, 2))*pow(fabs(u_1), 1.0), 2)*exp(0.63245553203367599*fabs(u_1))*pow(sin(0.10000000000000001*pow(u_1, 2)), 2)); return wert; // Rueckgabewert der Funktion f_2 } // Ende der Funktion f_2 int main(){ // Hauptfunktion Achterbahn_1 Wagen_0 { 0, 15, 5000, 0.01, 30.42*1000/(60*60) }; // Konstruktor erzeugt die zeitliche Entwicklung eines Wagens auf der Achterbahn vector<double> Zeit = Wagen_0.get_zeit(); // Aufrufen der Member-Funktion get_zeit() und kopieren der Zeitwerte vector<double> x = Wagen_0.get_u_1(); // Aufrufen der Member-Funktion et_u_1() und kopieren der Loesungswerte vector<double> v_x = Wagen_0.get_u_2(); // Aufrufen der Member-Funktion et_u_2() und kopieren der Loesungswerte printf("# 0: Index i \n# 1: t-Wert \n# 2:x(t) \n"); // Beschreibung der ausgegebenen Groessen printf("# 3: v_x(t) \n"); // (i, t, x, v_x) for(int i=0; i <Zeit.size(); ++i){ // for-Schleife zur Terminalausgabe der Loesung printf("%4d %19.15f %19.15f %19.15f \n",i, Zeit[i], x[i], v_x[i]); } } // Ende der Hauptfunktion
Im Hauptprogramm wird mittels des Konstruktors ' Achterbahn_1 Wagen_0 { 0, 15, 5000, 0.01, 30.42*1000/(60*60) };' ein Wagen mit den Anfangswerten der Teilaufgabe erzeugt und mit $N=5000$ Gitterpunkten im Intervall $t \in [0,15]$ numerisch berechnet.
Der Konstruktor initialisiert dabei nicht nur diese Werte, sondern generiert bei Erzeugung des Objektes vector-Standard Container, die die $5001$ Zeitgitterwerte ($t_i \, , \,\, i \in [0,1,2, ..., N]$, implementiert durch 'vector<double> Zeit;') der numerischen Lösung $\vec{x}(t_i)$ (vector<double> u_RungeK_4_1;) und $\dot{\vec{x}}(t_i)$ (vector<double> u_RungeK_4_2;) als private Daten-Member der Klasse speichern.
Nach der Instanzbildung des Wagens, mit dem Namen 'Wagen_0', werden die berechneten Werte an drei vector-Standard Container übergeben. Dies geschiet mit dem Aufruf der öffentlichen Member-Funktionen des Zeit-Vektors 'get_zeit(): vector<double> Zeit = Wagen_0.get_zeit();', des $\vec{x}$-Vektors (get_u_1(): vector<double> x = Wagen_0.get_u_1();) und des $\dot{\vec{x}}$-Vektors (get_u_2(): vector<double> v_x = Wagen_0.get_u_2();). Diese Lösungsvektoren wurden zuvor in der Klasse 'Achterbahn_1' beim Aufruf des Konstruktors berechnet. Bei der Instanzbildung wurden die Anzahl der Elemente in den Lösungsvektoren zunächst mittels des Befehls '.resize( N + 1 )' auf 'N+1' erhöht und dann wurden die enzelnen Werte in sie eingetragen.
In einer veralteten Version der Musterlösung dieser Teilaufgabe (siehe C++ Programm Achterbahn_1_old.cpp und hpp-Datei dsolve_Sys_1.hpp) wurde die ausgelagerte Klasse noch 'dsolve_Sys_1' genannt und die Lösungs-Standardvektoren wurden mittels '.push_back(...)' mit Werten aufgefüllt. Der hier gewählte Weg ist für den Programmablauf vorteilhafter, da die im dynamischen Speicher bereitgestellte Größe der Lösungsvektoren sich während der Simulation sich nicht ständig anpassen muss.
4. Teilaufgabe
Vergleichen Sie beide Simulationen quantitativ.
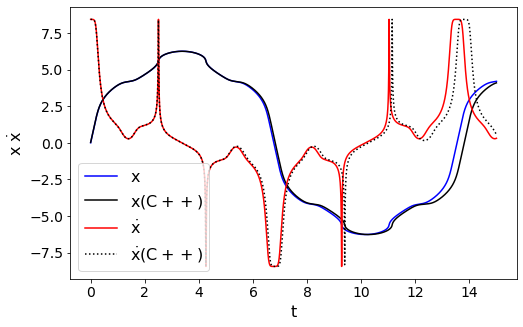
Am Ende werden die berechneten Daten im Terminal ausgegeben. Leitet man die Terminalausgabe in eine Datei 'Achterbahn_1.dat' um und liest sie in das Jupyter Notebook 'Achterbahn_2.ipynb' (View Notebook, Download Notebook) ein, so kann man die numerische Lösung des C++ Programms mit den Python Simulationen vergleichen. Die nebenstehende Abbildung wurde mittels dieses Notebooks generiert und sie stellt die numerische Python Lösung ($N=100000$, blaue Kurve $\vec{x}(t)$ und rote Kurve $\dot{\vec{x}}(t)$) im Vergleich zu den Ergebnissen des C++ Programmes ($N=5000$, , schwarze durchgehende Kurve $\vec{x}(t)$ und schwarze gepunktete Kurve $\dot{\vec{x}}(t)$) dar. Man erkennt ein leichtes Abweichen der C++ Resultate bei späten Zeiten, wobei man durch Erhöhung von $N$ zu den Python Resultaten konvergiert.
5. Teilaufgabe
Verallgemeinern Sie das C++ Programm so, dass mehrere Wagen auf der Achterbahn fahren können. Simulieren Sie ein System bestehend aus zwei wechselwirkungsfreien Wagen (siehe obige Animation) und benutzen Sie dabei für den ersten Wagen $i=0 \, , \, \tau_0 = 0 $ und $\dot{x}_0(0) = 16.45 \, [m/s]$ (blauer Wagen) und für den zweiten Wagen den ersten Wagen $i=1 \, , \, \tau_1=2 \, [s] $ und $\dot{x}_1(2) = 5.5 \, [m/s]$ (grüner Wagen).
Die in der vorigen Teilaufgabe konstruierte Klasse hatte die Eigenheit, dass sie im Anweisungsblock des Konstruktors die gesamte Berechnung der Wagenbewegung direkt bei Instanzbildung ausführte. Im Hinblick auf die weiteren Teilaufgaben (speziell das spätere Implementieren des elastischen Stoßes der beiden Wagen) ist es vorteilhaft, die Berechnung der numerischen Zeitschritte nach und nach zu erledigen und erst nach der Instanzbildung der Objekte durchzuführen. Auch hatten wir in der vorigen Teilaufgabe gesehen, dass es für eine genaue Berechnung eine größere Anzahl als $5000$ Gitterpunkte benötigt, man jedoch auch nicht zu viele Datenwerte im Terminal ausgeben möchte.
Die Erweiterung des Programms auf mehrere Wagen wurde möglichst allgemein gehalten, damit z.B. eine weitere Einfügung eines dritten oder vierten Wagens einfach möglich ist. Die folgenden C++ Quelltexte (Achterbahn_2.cpp und Achterbahn_2.hpp) stellen eine Verallgemeinerung, der in der vorigen Teilaufgabe beschriebenen Programme, auf mehrere Wagen dar und wenden diese auf die oben angegebenen Anfangsbedingungen an.
Der Konstruktor der neuen Klasse 'Achterbahn_2' enthält nun fünf Argumente ( Achterbahn_2(double t_, double alpha_1_, double alpha_2_, int N_sim_) : ... { ...} ), die Anfangszeit, den Anfangsort und die Anfangsgeschwindigkeit des Wagens und die Anzahl der ausgegebenen Elemente der Lösungsvektoren. Im Gegensatz zu dem vorigen Konstruktor werden bei dessen Aufruf lediglich die Anfangswerte in die jeweiligen privaten Daten-Member initialisiert. Die eigentliche Berechnung und das Auffüllen der Lösungs-vector-Container erfolgt über eine öffentlich aufrufbare Memberfunktion 'Gehe_Zeitschritt(..)', die mittels einer Runge-Kutta Ordnung vier Methode einen gewissen Zeitbereich vorausberechnet und den letzten Punkt dieser Berechnung in die Lösungs-vector-Container als neues Element einfügt. Zusätzlich zu dieser Methode wurde eine weitere Funktion ' Ruhe_Zeitschritt()' implementiert (um dem verspäteten "in die Bahn katapultieren' des zweiten Wagens gerecht zu werden. Die DGL bestimmende Funktion wurde in der Klasse als eine virtuelle Funktion deklariert (näheres über virtuelle Funktionen und abstrakte Klassen finden Sie im zweiten Unterpunkt dieser Vorlesung), wobei die Definition dieser Funktion sich in der Datei Achterbahn_2.cpp befindet, sodass der Benutzer sie gegebenenfalls noch abändern kann, ohne die Klasse 'Achterbahn' verändern zu müssen.
/* Klasse zur Berechnung der Loesung einer Differentialgleichung der Form y''=f_2(t,y) * mittels Runge-Kutta Ordnung vier Verfahren * Verfahren zur Loesung der DGL ist in eine Klasse ausgelagert * Zeitentwicklung mittels einer Methode Gehe_Zeitschritt(...) * Konstruktor: Achterbahn_2(Anfangszeit a, Anfangswert1 alpha_1=y(a)=u_1(a), Anfangswert2 alpha_2=y'(a)=u_2(a), Anzahl der Zeitgitterpunkte der Simulation) */ #include <stdio.h> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <vector> // Vector-Container der Standardbibliothek class Achterbahn_2{ //Definition der Klasse 'Achterbahn_2' double t = 0; double alpha_1 = 0.0; // 1.Anfangswert bei t=a: u_1(a)=alpha_1 double alpha_2 = 0.0; // 2.Anfangswert bei t=a: u_2(a)=alpha_2 double k1_1,k2_1,k3_1,k4_1; // Deklaration der vier Runge-Kutta Parameter fuer u_1 double k1_2,k2_2,k3_2,k4_2; // Deklaration der vier Runge-Kutta Parameter fuer u_2 int index = 0; int N_sim = 2500; // Anzahl der Gitter-Zeitpunkte der Simulation (Dimension der folgenden Loesungsvektoren) std::vector<double> u_RungeK_4_1; // Deklaration eines double Vektors zum Speichern der Loesung fuer u_1 std::vector<double> u_RungeK_4_2; // Deklaration eines double Vektors zum Speichern der Loesung fuer u_2 std::vector<double> Zeit; // Deklaration eines double Vektors zum Speichern der Zeit-Werte public: // Konstruktor mit fuenf Argumenten (Initialisierung der Parameter, Berechnung der Loesung der DGL) Achterbahn_2(double t_, double alpha_1_, double alpha_2_, int N_sim_) : t(t_),alpha_1(alpha_1_),alpha_2(alpha_2_),N_sim(N_sim_) { Zeit.resize( N_sim + 2 ); // Die Anzahl der Eintraege im Vektor wird auf N+2 erhoeht u_RungeK_4_1.resize( N_sim + 2 ); // Die Anzahl der Eintraege im Vektor wird auf N+2 erhoeht u_RungeK_4_2.resize( N_sim + 2 ); // Die Anzahl der Eintraege im Vektor wird auf N+2 erhoeht Zeit[0] = t_; // Zum Zeit-Vektor die Endzeit eintragen u_RungeK_4_1[0] = alpha_1; // Zum y-Vektor den Anfangswert alpha_1=y(a) eintragen u_RungeK_4_2[0] = alpha_2; // Zum y'-Vektor den Anfangswert alpha_2=y'(a) eintragen }; // Ende des Konstruktors double f_1(double t, double u_1, double u_2){ // Deklaration und Definition der Funktion f_1(t,u_1,u_2) double wert; wert = u_2; // Eigentliche Definition der Funktion return wert; // Rueckgabewert der Funktion f_1 } // Ende der Funktion f_1 virtual double f_2(double t, double u_1, double u_2); // Deklaration der virtuellen Member-Funktion f_1(t,y) (Definition findet ausserhalb der Klasse statt) double get_zeit(int element) const { return Zeit[element]; } // Definition der konstanten Member-Funktion get_zeit(i), Rueckgabewert i-ter Zeitpunkt double get_u1(int element) const { return u_RungeK_4_1[element]; } // Definition der konstanten Member-Funktion get_u1(i), Rueckgabewert i-ter Wert y(t_i)=u_1(t_i) der DGL double get_u2(int element) const { return u_RungeK_4_2[element]; } // Definition der konstanten Member-Funktion get_u2(i), Rueckgabewert i-ter Wert y'(t_i)=u_2(t_i) der DGL //Oeffentliche Methode Ruhe_Zeitschritt( ...) void Ruhe_Zeitschritt(double h_){ Zeit[index] = Zeit[index] + h_; // Zum Zeit-Vektor die neue Zeit eintragen u_RungeK_4_1[index+1] = u_RungeK_4_1[index]; // Zum y-Vektor den neuen Wert eintragen u_RungeK_4_2[index+1] = u_RungeK_4_2[index]; // Zum y'-Vektor den neuen Wert eintragen index++; // index um eins erhoehen } //Oeffentliche Methode Gehe_Zeitschritt( ...) void Gehe_Zeitschritt(double a, double b, int N){ double h = (b - a)/N; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) double u_1 = u_RungeK_4_1[index]; // Definition der lokalen Variable u_1=y und Initialisierung mit dem letzten berechneten Wert double u_2 = u_RungeK_4_2[index]; // Definition der lokalen Variable u_2=y' und Initialisierung mit dem letzten berechneten Wert Zeit[index] = a; // Zum Zeit-Vektor den aktuellen Zeitwert eintragen for(int i=0; i < N; ++i){ // for-Schleife ueber die einzelnen Punkte des t-Intervalls t = a + i*h; // Zeit-Parameter wird um h erhoeht k1_1 = h*f_1(t,u_1,u_2); // Runge-Kutta Parameter k1 fuer u_1 k1_2 = h*f_2(t,u_1,u_2); // Runge-Kutta Parameter k1 fuer u_2 k2_1 = h*f_1(t+h/2,u_1+k1_1/2,u_2+k1_2/2); // Runge-Kutta Parameter k2 fuer u_1 k2_2 = h*f_2(t+h/2,u_1+k1_1/2,u_2+k1_2/2); // Runge-Kutta Parameter k2 fuer u_2 k3_1 = h*f_1(t+h/2,u_1+k2_1/2,u_2+k2_2/2); // Runge-Kutta Parameter k3 fuer u_1 k3_2 = h*f_2(t+h/2,u_1+k2_1/2,u_2+k2_2/2); // Runge-Kutta Parameter k3 fuer u_2 k4_1 = h*f_1(t+h,u_1+k3_1,u_2+k3_2); // Runge-Kutta Parameter k4 fuer u_1 k4_2 = h*f_2(t+h,u_1+k3_1,u_2+k3_2); // Runge-Kutta Parameter k4 fuer u_2 u_1 = u_1 + (k1_1 + 2*k2_1 + 2*k3_1 + k4_1)/6; u_2 = u_2 + (k1_2 + 2*k2_2 + 2*k3_2 + k4_2)/6; } // Ende for-Schleife ueber die einzelnen Punkte des t-Intervalls u_RungeK_4_1[index+1] = u_1; // Zum y-Vektor den neuen Wert eintragen u_RungeK_4_2[index+1] = u_2; // Zum y'-Vektor den neuen Wert eintragen index++; // index um eins erhoehen } // Ende der Funktion Gehe_Zeitschritt( ...) }; // Ende der Klasse
// Musterlösung Projekt Achterbahn (Aufgabe 1) /* Berechnung der Lösung einer Differentialgleichung der Form x'=f(t,x) * mittels Runge-Kutta Ordnung vier Verfahren * Verfahren zur Loesung der DGL ist in eine Klasse ausgelagert * Zeitentwicklung der fuer unterschiedliche t-Werte in [a,b] * Zwei Wagen werden als Instanzen der Klasse Achterbahn_2 in einem vector-Container definiert */ #include "Achterbahn_2.hpp" // Einbinden der Klasse die das System der DGLs mittels Runge-Kutta Ordnung vier loest #include <stdio.h> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <vector> // Vector-Container der Standardbibliothek using namespace std; // Benutze den Namensraum std double Achterbahn_2::f_2(double t, double u_1, double u_2){ // Deklaration und Definition der Funktion f_2(t,u_1,u_2), berechnet mittels des Jupyter Notebooks Achterbahn.ipynb double wert; wert = 0.20000000000000001*u_1*(-32.0*pow(u_1, 4)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*pow(cos(0.10000000000000001*pow(u_1, 2)), 3) + 16.0*pow(u_1, 4)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*cos(0.10000000000000001*pow(u_1, 2)) + 75.894663844041105*pow(u_1, 2)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*pow(sin(0.10000000000000001*pow(u_1, 2)), 3)*fabs(u_1) + 80.0*pow(u_1, 2)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*pow(sin(0.10000000000000001*pow(u_1, 2)), 3) - 63.245553203367592*pow(u_1, 2)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*sin(0.10000000000000001*pow(u_1, 2))*fabs(u_1) - 80.0*pow(u_1, 2)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*sin(0.10000000000000001*pow(u_1, 2)) + 60.0*pow(u_1, 2)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*pow(cos(0.10000000000000001*pow(u_1, 2)), 3) - 60.0*pow(u_1, 2)*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*cos(0.10000000000000001*pow(u_1, 2)) - 1962.0*pow(u_1, 2)*exp(0.316227766016838*fabs(u_1))*cos(0.10000000000000001*pow(u_1, 2)) - 15.811388300841898*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*pow(sin(0.10000000000000001*pow(u_1, 2)), 3)*fabs(u_1) + 63.245553203367592*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*pow(cos(0.10000000000000001*pow(u_1, 2)), 3)*fabs(u_1) - 63.245553203367592*pow(u_2, 2)*exp(0.63245553203367599*fabs(u_1))*cos(0.10000000000000001*pow(u_1, 2))*fabs(u_1) - 1551.0971923125903*exp(0.316227766016838*fabs(u_1))*sin(0.10000000000000001*pow(u_1, 2))*fabs(u_1))*sin(0.10000000000000001*pow(u_1, 2))/(100.0*pow(u_1, 2) + pow(4.0*pow(u_1, 2)*cos(0.10000000000000001*pow(u_1, 2)) + 3.1622776601683795*sin(0.10000000000000001*pow(u_1, 2))*pow(fabs(u_1), 1.0), 2)*exp(0.63245553203367599*fabs(u_1))*pow(sin(0.10000000000000001*pow(u_1, 2)), 2)); return wert; // Rueckgabewert der Funktion f_2 } // Ende der Funktion f_2 int main(){ // Hauptfunktion double a = 0; // Untergrenze des Zeit-Intervalls [a,b] in dem die Loesung berechnet werden soll double b = 20; // Obergrenze des Intervalls [a,b] int N_RK = 100; // Anzahl der Gitter-Zeitpunkte des Runge-Kutta Ordnung vier Verfahrens int N_sim = 2500; // Anzahl der Gitter-Zeitpunkte der Simulation (Anzahl der ausgegebenen Punkte) double h_sim = (b - a)/N_sim; // Abstand dt zwischen den aequidistanten Punkten des Sim-Intervalls (h=dt) double t; // Aktueller Zeitwert vector<double> tau = {0.0, 2.0 }; // Deklaration eines double Vektors zum Speichern der Anfangszeiten der sechs Wagen vector<double> v_0 = {16.45, 5.5 }; // Deklaration eines double Vektors zum Speichern der Anfangszeiten der sechs Wagen vector<Achterbahn_2> Wagen; // Deklaration eines vector-Containers der Wagen for (unsigned int n = 0; n < tau.size(); ++n){ // for-Schleife zum Auffuellen des Containers mit Wagen-Elementen Wagen.push_back( Achterbahn_2 {a, 0.01, v_0[n], N_sim } ); // Initialisierung der Wagen und einfuegen in den Container } // Ende for-Schleife for(int i = 0; i <= N_sim; ++i){ // for-Schleife ueber die Simulations-Zeitpunkte t = a + i * h_sim; // Zeit-Parameter wird um h_sim erhoeht for(unsigned int n = 0; n < tau.size(); ++n){ // for-Schleife ueber die einzelnen Wagen if( t >= tau[n] ){ // if-Anweisung: Ist Wagen schon auf der Achterbahn? Wagen[n].Gehe_Zeitschritt(t, t+h_sim, N_RK); // Aufruf der Runge-Kutta-Methode 'Gehe_Zeitschritt(...)' in der Klasse Achterbahn_2 } else { // else-Anweisung: Ist Wagen schon auf der Achterbahn? Wagen[n].Ruhe_Zeitschritt(h_sim); // Aufruf der Runge-Kutta-Methode 'Ruhe_Zeitschritt(...)' in der Klasse Achterbahn_2 } // Ende else-Anweisung } // Ende for-Schleife ueber die einzelnen Wagen } // Ende for-Schleife ueber die Simulations-Zeitpunkte printf("# 0: Index i \n# 1: t-Wert \n"); // Beschreibung der ausgegebenen Groessen printf("# 2: x(t), Wagen 1 \n# 3: v_x(t), Wagen 1 \n"); printf("# 4: x(t), Wagen 2 \n# 5: v_x(t), Wagen 2 \n"); for(int i=0; i <= N_sim; ++i){ // for-Schleife zur Terminalausgabe der Loesung (Zeitgitterpunkte) printf("%5d %19.15f ",i, Wagen[0].get_zeit(i)); // Ausgabe der Simulierten Zeitwerte mittels der Methode get_zeit() for(auto& n : Wagen){ // for-Schleife zur Terminalausgabe der Loesung (Wagen) printf("%19.15f %19.15f ", n.get_u1(i), n.get_u2(i)); // Ausgabe der Simulierten Orts- und Geschwindigkeitswerte mittels der Methoden n.get_u_1() und n.get_u_2() } // Ende for-Schleife (Wagen) printf("\n"); } // Ende for-Schleife (Zeitgitterpunkte) } // Ende der Hauptfunktion
Die oben abgebildeten C++ Quelltexte unterscheiden sich von den Quelltexten der ersten, veralteten Müsterlösung ( siehe Achterbahn_2_old.cpp und dsolve_Sys_2.hpp) durch eine Performance-Verbesserung. In der alten Version wurden die Elemente der privaten Klassenmember mittels der const Methoden 'n.get_u_1()[i]' und ' n.get_u_2()[i]' im Terminal ausgegeben (z.B. mittels 'vector
In dem Hauptprogramm Achterbahn_2.cpp wurde zwei Gitterpunktsvariablen definiert. $N_{RK}$ 'int N_RK = 100;' beschreibt hierbei die Anzahl der Gitter-Zeitpunkte des Runge-Kutta Ordnung vier Verfahrens und $N_{sim}$ 'int N_sim = 2500; ' die Anzahl der Gitter-Zeitpunkte der Simulation (Anzahl der im Terminal ausgegebenen Punkte). Effektiv besitzt die durchgeführte Berechnung somit $N=N_{sim} \cdot $N_{RK}$ = 250000$ Zeitgitterpunkte, wobei im Terminal lediglich $2500$ Datenpunkte ausgegeben werden.
for (unsigned int n = 0; n < tau.size(); ++n){
Wagen.push_back( Achterbahn_2 {a, 0.01, v_0[n], N_sim } );
}
Zusätzlich wird im Hauptprogramm ein eigener vector-Container bestehend aus Elementen des Typs unsrer Klasse 'dsolve_Sys_2' erzeugt. Da die Elemente dieses Containers die einzelnen Wagen repräsentieren werden, wurde als Name des Containers 'Wagen gewählt (vector<dsolve_Sys_2> Wagen; ). Die Anfangszeiten $\tau_i$ und Anfangsgeschwindigkeiten $\dot{x}_i(\tau_i)$ der Wagen wurden im Hinblick auf mehrere Wagen als vector-Container definiert. Das Auffüllen des Wagen-Containers und die Instanzbildung der Wagen erfolgt der Allgemeinheit halber innerhalb der, oben rechts abgebildeten for-Schleife.
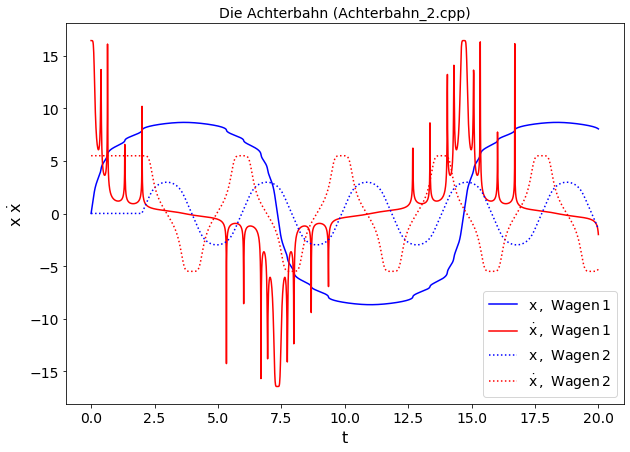
Die zeitliche Simulation über die $N_{sim}$ Simulationspunkte beginnt in der for-Schleife 'for(int i = 0; i <= N_sim; ++i){ ...}' wobei zwischen den jeweiligen Simulationszeitpunkten die zeitliche Entwicklung des Systems mittels der Runge-Kutta Ordnung vier Methode mit $N_{RK}$ Zeitgitterpunkten berechnet wird. Diese Berechnung wird innerhalb der for-Schleife, die über die einzelnen Wagen der Achterbahn geht, durchgeführt ( for(unsigned int n = 0; n < tau.size(); ++n){ ... } ) und durch den Aufruf der Funktion 'Wagen[n].Gehe_Zeitschritt(...) eingeleitet. Die obere linke Abbildung zeigt die berechneten Simulationswerte der beiden Wagen, wobei der erste Wagen durch die durchgezogenen Kurven und der zweite Wagen durch die gepunkteten Kurven beschrieben wird.
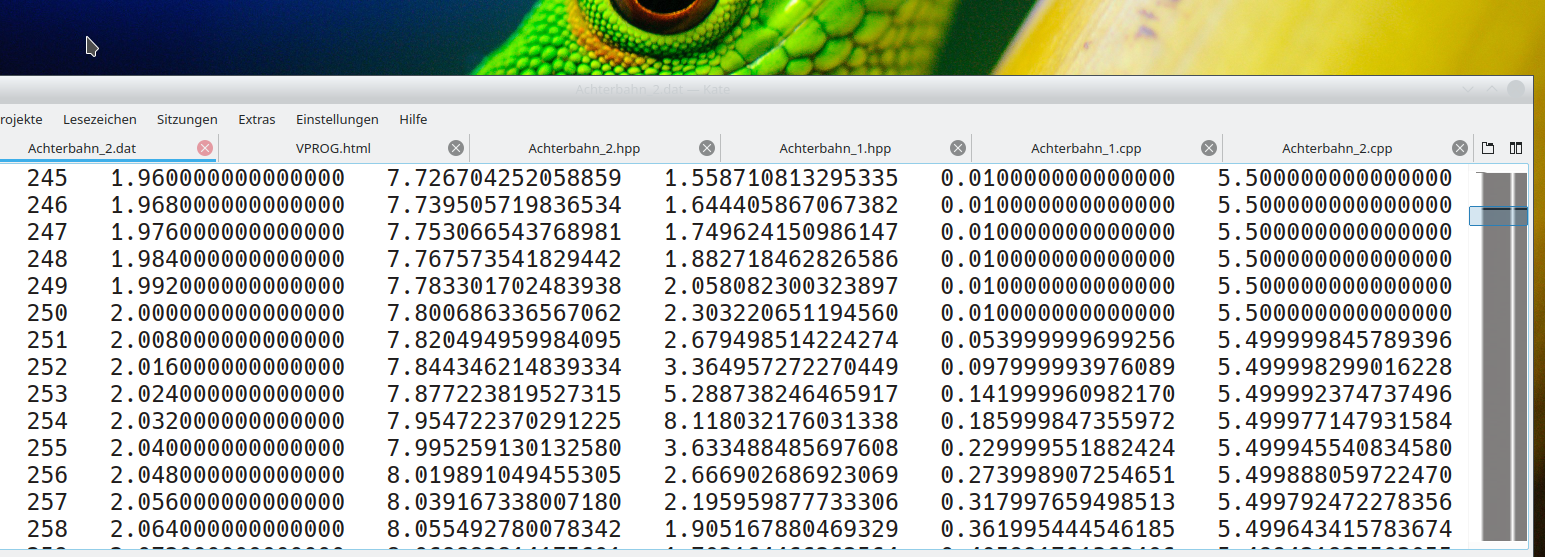
Die berechneten Daten des C++ Programms (siehe untere Abbildung) kann man nun auch wieder mittels des Jupyter Notebooks 'Achterbahn_2.ipynb' (View Notebook, Download Notebook) als Animation visualisieren (siehe unteres Video).
6. Teilaufgabe
Um die Richtigkeit der berechneten Daten des C++ Programmes zu verifizieren, führen Sie (nur in dieser Teilaufgabe) eine separate Simulation mit abgeänderter Achterbahnform durch, bei der es eine analytische Lösung gibt. Berechnen Sie zunächst auf analytischem Weg, mittels eines Jupyter Notebooks unter Verwendung der SymPy Bibliothek, die Euler-Lagrange Gleichungen der Bewegung eines Massenpunktes der Masse $m$ auf einer Zykloidenbahn (siehe Aufgabe 15.7: Walter Greiner, 'Klassische Mechanik II' [8. Auflage, 2008, Kapitel V15. Seite 271]). Der Massepunkt gleitet reibungsfrei auf einer Zykloide , die durch $$ \begin{equation} x(\theta) = a \left( \theta - \hbox{sin}(\theta) \right) \,\, , \,\, y(\theta) = a \left( 1 + \hbox{cos}(\theta) \right) \,\, , \quad 0 \leq \theta(t) \leq 2 \pi \end{equation} $$ gegeben ist. Vergleichen Sie Ihre Werte mit der analytischen Lösung in Aufgabe 15.7 (Walter Greiner, 'Klassische Mechanik II' [8. Auflage, 2008, Kapitel V15. Seite 271]). Vergleichen Sie auch die Resultate einer entsprechenden Simulation mittels Ihres C++ Programmes.
Gerne können Sie auch dieses Projekt weiter bearbeiten und einige der noch nicht bearbeiteten Teilaufgaben lösen ...
7. Teilaufgabe
Implementieren Sie nun einen elastischen Stoß der zwei Wagen in Ihr C++ Programm und führen Sie die obere Animation nochmals durch.
.....
8. Teilaufgabe
Vernachlässigen Sie nun nicht mehr die Luftreibung und bauen Sie einen zusätzlichen Reibungsterm in die Lagrangedichte ein. Lösen die dann die resultierenden Bewegungsgleichungen numerisch. Die Länge der Achterbahn sein $l=30 \, [m]$. Berechnen Sie, mit welcher maximalen Anfangsgeschwindigkeit der erste Wagen in die Bahn katapultiert werden kann.
.....
9. Teilaufgabe
Der Verlauf der Metallschiene der Achterbahn wird nun durch ein Lagrangepolynom $h(x)$ beschrieben, welches durch die Punkte $\vec{x}$ und $\vec{y}$ geht. Implementieren Sie in ihr C++ Programm die Fälle, dass vier bzw. fünf Punkte vorgegeben sind.
.....
10. Teilaufgabe
In einem der Wagen befindet sich jetzt ein physikalisches Pendel. Beschreiben Sie die Bewegung des Pendels innerhalb des Wagens.
.....
11. Teilaufgabe
Schreiben Sie Ihr Programm so um, dass das Projekt Achterbahn eine Klasse (mit eigenen Daten-Member, Member Funktionen und Konstruktoren) repräsentiert.
.....