Musterlösung zum Übungsblatt Nr. 3
Musterlösung zur Aufgabe 1 (10 Punkte)
Das folgende C++ Programm stellt eine Musterlösung zur Aufgabe 1 dar:
// Musterlösung der Aufgabe 3 des Übungsblattes Nr.1 /* Konvergenzverhalten der geometrischen Reihe * Ausgabe zum Plotten (Gnuplot oder Python) mittels: "./a.out > A3_1.dat" */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) int main(){ // Hauptfunktion const double q = 8.0/9; // Definition von q als konstante double Zahl unsigned int k; // Deklaration des Summenindex als ganze Zahl const unsigned int N = 100; // Definition der Anzahl der mitgenommenen Summenglieder als konstante ganze Zahl double wert_approx = 0; // Definition der approximierten Wertes der printf("# 0: Summenindex k \n# 1: Approximierter Wert der Summe \n"); // Beschreibung der ausgegebenen Groessen for(k=0; k<=N; ++k){ // Schleife zur Berechnung der Summe wert_approx = wert_approx + pow(q,k); // Innerer Teil der geometrischen Reihe printf("%4i %20.15f \n",k, wert_approx); // Ausgabe des approximierten Wertes } // Ende der Schleife printf("# Approximierter Wert der Summe: %20.15f \n", wert_approx); // Ausgabe des approximierten Wertes printf("# Wert im Limes der geometrischen Reihe: %20.15f \n", 1.0/(1-q)); // Ausgabe des wirklichen Wertes }
Die Variable 'q' wurde als eine konstante Größe definiert ( const double q ) und die eigentliche Berechnung der Reihe mittels einer for-Schleife programmiert ( for(k=0; k<=N; ++k){ ...} ).
Das folgende Bild zeigt das Ende der Terminalausgabe nachdem das Programm ausgeführt wurde.
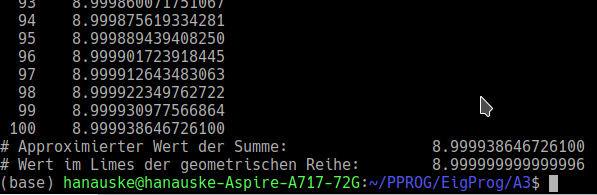
Man erkennt schon hier, dass der approximierte Wert nach 100 Folgengliedern gut mit dem Grenzwert der unendlich geometrischen Reihe ($\frac{1}{1-q} = \frac{1}{1-\frac{8}{9}} = \frac{1}{\frac{1}{9}} = 9$) übereinstimmt.
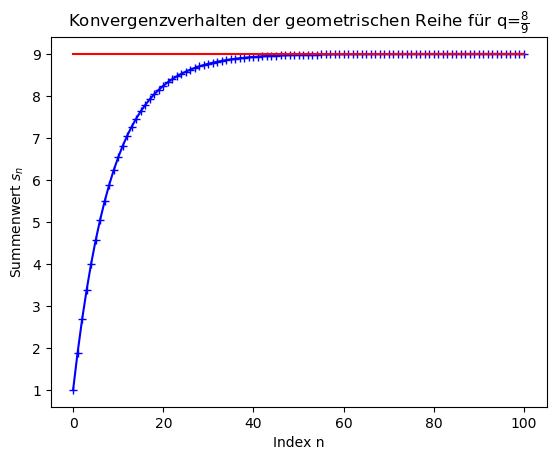
Um die Daten zu visualisieren, leiteten wir diese Terminalausgabe in eine Datei um ' ./a.out > A3_1.dat '. Für die Visualisierung des Konvergenzverhaltens der geometrischen Reihe verwendeten wir das unten angegebene Python-Skript, welches die links abgebildete Grafik erstellt. Man erkennt, dass sich schon nach ca. 40 Folgengliedern der Partialsumme unserer geometrischen Reihe, der Wert nur noch geringfügig ändert und dem analytischen Wert von 9 (rote Linie) entspricht.
# Python Programm zum Plotten der berechneten Daten von (A3_1.cpp) import matplotlib.pyplot as plt # Python Bibliothek zum Plotten (siehe https://matplotlib.org/ ) import numpy as np # Python Bibliothek fuer Mathematisches (siehe https://numpy.org/ ) data = np.genfromtxt("./A3_1.dat") # Einlesen der berechneten Daten von A3_1.cpp q=8/9 # Festlegung des q-Wertes fuer den Vergleich plt.title(r'Konvergenzverhalten der geometrischen Reihe für q=$\frac{8}{9}$') # Titel der Abbildung plt.ylabel(r'Summenwert $s_n$') # Beschriftung y-Achse plt.xlabel('Index n') # Beschriftung x-Achse plt.plot(data[:,0],data[:,1], marker='+', color="blue") # Plotten der Daten plt.plot([data[0,0],data[-1,0]],[1/(1-q),1/(1-q)], color="red") # Horizontale Linie: exakter Wert der unendlich geometrischen Reihe plt.savefig("PythonPlot_A3_1.png", bbox_inches="tight") # Speichern der Abbildung als Bild plt.show() # Zusaetzliches Darstellen der Abbildung in einem separaten Fenster
Musterlösung zur Aufgabe 2 (5 Punkte)
Das im Unterpunkt Anwendungsbeispiel: Folgen und Reihen verwendete C++ Programm While_2.cpp wurde unter Verwendung einer for-Schleife wie folgt umgeschrieben.
/* Mittels der Leibniz-Reihe * (Gottfried Wilhelm Leibniz, Zeitschrift Acta Eruditorum, 1682) * wird die Kreiszahl Pi approximiert * (Anzahl der Summanden = N) * Ausgabe zum Plotten (Gnuplot oder Python) mittels: "./a.out >> While_2.dat" */ #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) int main(){ // Hauptfunktion unsigned int k; // Deklaration des Summenindex als ganze Zahl const unsigned int N = 100; // Definition der Anzahl der mitgenommenen Summenglieder als konstante ganze Zahl double Pi_Approx = 0; // Definition der approximierten Gleitkommazahl von Pi (Datentyp 'double') printf("# 0: Summenindex k \n# 1: Approximierter Wert von Pi \n"); // Beschreibung der ausgegebenen Groessen for(k=0; k<=N; ++k){ // For-Schleife zur Berechnung von Pi/4 Pi_Approx = Pi_Approx + pow(-1,k)/(2*k + 1); // Innerer Teil der Leibniz-Reihe printf("%4i %20.15f \n",k, 4*Pi_Approx); // Ausgabe des approximierten Wertes von Pi } // Ende der Schleife Pi_Approx = Pi_Approx*4; // Leibniz-Reihe liefert Pi/4, deshalb hier mal 4 printf("# Approximierter Wert von Pi: %20.15f \n", Pi_Approx); // Ausgabe des approximierten Wertes printf("# Wirklicher Wert von Pi: %20.15f \n", M_PI); // Ausgabe des wirklichen Wertes }
Musterlösung zur Aufgabe 3 (5 Punkte)
Die folgenden Ausdrücke wurden mittels eines C++ Programms auf 15 Stellen genau berechnet \[ \begin{equation} \sum_{k=0}^{2536} \left( \frac{1}{2} \right)^k \quad,\quad \sum_{k=3}^{45} k^{\frac{3}{5}} \quad,\quad \sum_{k=-5}^{20} \frac{k^5}{e^{-k} + 1} \quad . \end{equation} \] Das C++ Programm sah wie folgt aus
// Musterlösung der Aufgabe 3 des Übungsblattes Nr.3 #include <iostream> // Ein- und Ausgabebibliothek #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) int main(){ // Hauptfunktion int k , N; // Deklaration des Summenindex und Anzahl Summenglieder double A_1 = 0; // Deklaration der double Variable für Aufgabe 2.1 und Initialisierung double A_2 = 0; // Deklaration der double Variable für Aufgabe 2.2 und Initialisierung double A_3 = 0; // Deklaration der double Variable für Aufgabe 2.3 und Initialisierung N=2536; for(k=0; k<=N; ++k){ // Schleifen Anfang A_1 = A_1 + pow(1.0/2,k); // Reihe 1 } // Schleifen Ende N=55; for(k=3; k<=N; ++k){ // Schleifen Anfang A_2 = A_2 + pow(k,3.0/5); // Reihe 2 } // Schleifen Ende N=20; for(k=-5; k<=N; ++k){ // Schleifen Anfang A_3 = A_3 + pow(k,5)/(exp(-k) + 1 ); // Reihe 3 } // Schleifen Ende // Terminal Ausgabe auf 15 Nachkommastellen printf("%-24s %-24s %-24s \n","Aufgabe 3.1","Aufgabe 3.2","Aufgabe 3.3"); printf("%-24.15f %-24.15f %-24.15f \n",A_1,A_2,A_3); }
und produzierte die folgende Terminalausgabe:
