Musterlösung zum Übungsblatt Nr. 12
Musterlösung zur Aufgabe 1 (20 Punkte)
In dem folgenden C++ Header File Pendel.hpp ist die Sub-Subklasse 'Pendel_getrieb' von der Subklasse 'Pendel' abgeleitet worden. Mittels der Klasse 'Pendel_getrieb' lassen sich Simulationen des periodisch angetriebenen Pendels erstellen.
/* Header-Datei (Übungsblatt 12) * Das physikalische und mathematische Pendel mit Reibung (Stokesscher Ansatz) * Berechnung der Lösung einer Differentialgleichung zweiter Ordnung * bzw. eines Systems von zwei Differentialgleichungen erster Ordnung * mittels der Runge-Kutta Ordnung vier Methode * Verfahren zur Loesung der DGL ist in einer abstrakten Basisklasse ausgelagert * Berechnung der Lösung innerhalb einer Methode (Klassenfunktion) Runge-Kutta-Verfahren * Überschreibung der virtuellen Funktion der Bewegungsgleichungen in der abgeleiteten Klasse (Subklasse) Pendel * Zeitentwicklung der fuer unterschiedliche t-Werte in [a,b] * Konstruktor: Pendel(Masse des Pendels, Länge des Pendels l, Reibung beta, Anfangszeit a, Endzeit b, Anzahl der Punkte N, Anfangswerte alpha) * bzw. Konstruktor: Pendel_math(...) oder Pendel_getrieb(...) */ #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <vector> // Vector-Container der Standardbibliothek using namespace std; // Benutze den Namensraum std // Abstrakte Basisklasse 'dsolve' class dsolve { public: // Daten-Member der Klasse double a; // Untergrenze des Zeit-Intervalls double b; // Obergrenze des Intervalls int N; // Anzahl der Punkte vector<double> alpha; // Anfangswerte vector<vector<double>> ym; // Lösungsmatrix vector<double> t; // Zeit-Vektor // Virtuelle Funktion dgls, wird an anderer Stelle definiert virtual vector<double> dgls(double t, vector<double> u_vec) = 0; // Konstruktor mit vier Argumenten (Initialisierung der Daten-Member) dsolve(double a_, double b_, int N_, vector<double> alpha_) :a(a_), b(b_), N(N_), alpha(alpha_) { t.push_back(a_); // Zum Zeit-Vektor die Anfangszeit eintragen ym.push_back(alpha_); // Zur Loesungs-Matrix die Anfangswerte eintragen } // Methode der Runge-Kutta-Methode void solve() { double h = (b - a)/N; // Abstand dt zwischen den aequidistanten Punkten des t-Intervalls (h=dt) int n = alpha.size(); // Anzahl der Anfangswerte bzw. DGL-Gleichungen (hier n=2) vector<double> k1(n),k2(n),k3(n),k4(n); // Deklaration der vier Runge-Kutta Parameter fuer jede Loesung vector<double> y(n); // Temporaerer Hilfsvektor for (int i = 0; i < N; ++i) { // for-Schleife ueber die einzelnen Punkte des t-Intervalls for (int j = 0; j < n; ++j) k1[j] = h * dgls(t[i], ym[i])[j]; // for-Schleife ueber die n Runge-Kutta k1-Parameter for (int j = 0; j < n; ++j) y[j] = ym[i][j] + k1[j] / 2; // Temporaerer Hilfsvektor for (int j = 0; j < n; ++j) k2[j] = h * dgls(t[i] + h / 2, y)[j]; // for-Schleife ueber die n Runge-Kutta k2-Parameter for (int j = 0; j < n; ++j) y[j] = ym[i][j] + k2[j] / 2; // Temporaerer Hilfsvektor for (int j = 0; j < n; ++j) k3[j] = h * dgls(t[i] + h / 2, y)[j]; // for-Schleife ueber die n Runge-Kutta k3-Parameter for (int j = 0; j < n; ++j) y[j] = ym[i][j] + k3[j]; // Temporaerer Hilfsvektor for (int j = 0; j < n; ++j) k4[j] = h * dgls(t[i] + h, y)[j]; // for-Schleife ueber die n Runge-Kutta k4-Parameter for (int j = 0; j < n; ++j) y[j] = ym[i][j] + (k1[j] + 2 * k2[j] + 2 * k3[j] + k4[j]) / 6; // Temporaerer Hilfsvektor ym.push_back(y); // Zum Loesungs-Vektor den neuen Wert eintragen t.push_back(a + (i + 1) * h); // Zum Zeit-Vektor die neue Zeit eintragen } // Ende for-Schleife ueber die einzelnen Punkte des t-Intervalls } // Ende des Methode 'solve()' }; // Ende der Klasse 'dsolve' // Sub-Klasse 'Pendel' class Pendel : public dsolve { public: double m; // Masse des Pendels double l; // Länge des Pendels double beta; // Reibungskoeffizient // Überschreibung der virtuellen Funktion dgls vector<double> dgls(double t, vector<double> u_vec) override { vector<double> du_dt(u_vec.size()); // Die zwei DGLs erster Ordnung werden als Standard-Vektor definiert du_dt[0] = u_vec[1]; // Zwei DGLs erster Ordnung du_dt[1] = - 9.81 / l * sin(u_vec[0]) - beta / m * u_vec[1]; // DGl des physikalischen Pendels mit Reibung (Stokesscher Ansatz) return du_dt; // Rueckgabewert der DGLs als Standard-Vektor } // Ende: Definition der Bewegungsgleichung // Konstruktor mit sieben Argumenten (Initialisierung der Instanzvariablen (m,l,beta), vier Argumente für dsolve) Pendel(double m_ = 1.0, double l_ = 1.0, double beta_ = 0.0, double a_ = 0, double b_ = 1, int N_ = 10, vector<double> alpha_ = {0.1, 0}) : dsolve(a_, b_, N_, alpha_), m(m_), l(l_), beta(beta_) {} // Methode der Ausgabe der kartesische Koordinaten des Pendels am Stützpunkt i vector<double> r(size_t i) { vector<double> w = {0.0,0.0}; if (i < t.size()) { w = {l*sin(ym[i][0]), -l*cos(ym[i][0])};} return w; } // Methode der Ausgabe der Geschwindigkeit des Pendels in kartesische Koordinaten am Stützpunkt i vector<double> v(size_t i) { vector<double> w = {0.0,0.0}; if (i < t.size()) { w = {l*cos(ym[i][0])*ym[i][1], l*sin(ym[i][0])*ym[i][1]};} return w; } }; // Ende der Unterklasse 'Pendel' //Definition der Sub-Sub-Klasse 'Pendel_math' (mathematische Pendel, harmonischer Oszillator) als abgeleitete Klasse der Unterklasse 'Pendel' class Pendel_math : public Pendel { public: // Konstruktor mit sieben Argumenten (Initialisierung der Instanzvariablen (m,l,beta), vier Argumente für dsolve) Pendel_math(double m_ = 1.0, double l_ = 1.0, double beta_ = 0.0, double a_ = 0, double b_ = 1, int N_ = 10, vector<double> alpha_ = {0.1, 0}) : Pendel(m_, l_, beta_, a_, b_, N_, alpha_){} // Überschreibung der virtuellen Funktion dgls vector<double> dgls(double t, vector<double> u_vec) override { vector<double> du_dt(u_vec.size()); // Die zwei DGLs erster Ordnung werden als Standard-Vektor definiert du_dt[0] = u_vec[1]; // Zwei DGLs erster Ordnung du_dt[1] = - 9.81 / l * u_vec[0] - beta / m * u_vec[1]; // DGl des mathematischen Pendels mit Reibung (Stokesscher Ansatz) return du_dt; // Rueckgabewert der DGLs als Standard-Vektor } // Ende: Definition der Bewegungsgleichung }; // Ende der Klasse 'Pendel_math' //Definition der Sub-Sub-Klasse 'Pendel_getrieb' als abgeleitete Klasse der Unterklasse 'Pendel' class Pendel_getrieb : public Pendel { public: // Zusätzliche Instanzvariablen double A; // Amplitude A der ausseren periodisch Kraft double Omega; // Frequenz Omega der ausseren periodisch Kraft // Konstruktor mit neun Argumenten (Initialisierung der Instanzvariablen (m,l,beta,A,Omega), vier Argumente für dsolve) Pendel_getrieb(double m_ = 1.0, double l_ = 1.0, double beta_ = 0.0, double A_ = 0.95, double Omega_ = 2.0/3.0, double a_ = 0, double b_ = 1, int N_ = 10, vector<double> alpha_ = {0.1, 0}) : Pendel(m_, l_, beta_, a_, b_, N_, alpha_), A(A_), Omega(Omega_) {} // Überschreibung der virtuellen Funktion dgls vector<double> dgls(double t, vector<double> u_vec) override { vector<double> du_dt(u_vec.size()); // Die zwei DGLs erster Ordnung werden als Standard-Vektor definiert du_dt[0] = u_vec[1]; // Zwei DGLs erster Ordnung du_dt[1] = A*cos(Omega*t) - 9.81 / l * sin(u_vec[0]) - beta / m * u_vec[1]; // DGl des periodisch angetriebenen Pendels mit Reibung (Stokesscher Ansatz) return du_dt; // Rueckgabewert der DGLs als Standard-Vektor } // Ende: Definition der Bewegungsgleichung }; // Ende der Klasse 'Pendel_getrieb'
Die eigentliche Instanzbildung des Objektes der Klasse 'Pendel_getrieb' und die konkrete Berechnung der Zeitentwicklung des periodisch angetriebenen Pendels wurde mittels der folgenden C++ Datei angefertigt.
// Das periodisch angetriebene Pendel (Übungsblatt 12) /* Beispiel eines schwingenden Systems aus dem Bereich der Mechanik * welches bei gewissen Parameterkonstellationen deterministisch chaotische Bewegungen zeigt * Berechnung der Loesung eines Systems von Differentialgleichungen * mittels Runge-Kutta Ordnung vier Verfahren * Verfahren zur Loesung der DGL ist in einer Klasse ausgelagert * Zeitentwicklung, t-Werte in [a,b] * Konstruktor mit neun Argumenten (Initialisierung der Instanzvariablen (m,l,beta,A,Omega), vier Argumente für dsolve) * Ausgabe zum Plotten mittels Python Skript PythonPlot_GetriebPendel.py */ #include "Pendel.hpp" // Header-Datei des physikalischen,mathematischen und periodisch angetriebenen Pendels mit Reibung (Stokesscher Ansatz) #include <iostream> // Standard Input- und Output Bibliothek in C, z.B. printf(...) using namespace std; // Hauptprogramm int main() { double m = 1.0; // Masse des Pendels double l = 9.81; // Länge des Pendels double beta = 0.5; // Reibungskoeffizient double A = 1.098; // Amplitude A der ausseren periodisch Kraft double Omega = 2.0/3.0; // Frequenz Omega der ausseren periodisch Kraft double a = 0; // Untergrenze des Zeit-Intervalls double b = 100; // Obergrenze des Intervalls int N = 100000; // Anzahl der Punkte FILE *ausgabe; // Deklaration eines Files fuer die Ausgabedatei ausgabe = fopen("GetriebenesPendel.dat", "w+"); // Ergebnisse werden in die Datei "GetriebenesPendel.dat" geschrieben Pendel_getrieb P_A = Pendel_getrieb(m,l,beta,A,Omega,a,b,N,{0,0}); // Konstruktor bilded eine Instanz der Klasse Pendel_getrieb P_A.solve(); // Methode der Runge-Kutta-Methode ausführen // Ausgabe in die Ausgabedatei, Beschreibung der ausgegebenen Groessen fprintf(ausgabe, "# 0: Index i \n# 1: t-Wert \n# 2: theta \n# 3:d_theta \n"); // Beschreibung der ausgegebenen Groessen fprintf(ausgabe, "# 2: x(t) , physikalisches Pendel \n# 3: y(t) , physikalisches Pendel \n"); fprintf(ausgabe, "# 4: v_x(t) , physikalisches Pendel \n# 5: v_y(t) , physikalisches Pendel \n"); // Ausgabe der Werte in die Ausgabedatei for(size_t i=0; i < P_A.t.size(); ++i){ if ((i % 50) == 0) { // nur jeden 10-ten Wert ausgeben lassen fprintf(ausgabe, "%3ld %19.15f %19.15f %19.15f ",i,P_A.t[i],P_A.ym[i][0],P_A.ym[i][1]); fprintf(ausgabe, "%19.15f %19.15f %19.15f %19.15f ",P_A.r(i)[0],P_A.r(i)[1],P_A.v(i)[0],P_A.v(i)[1]); fprintf(ausgabe, "\n"); } } fclose(ausgabe); // Schliessen der Ausgabedatei } // Ende Hauptprogramm
Die Ausgabe der Ergebnisse erfolgte dabei direkt in die Ausgabedatei 'GetriebenesPendel.dat'. Es wurde eine Pendel-Simulation mit $A=1.098$ erstellt und die berechneten Daten sind in der folgenden Abbildung mittels des Python-Skriptes PythonPlot_GetriebPendel.py visualisiert worden.
Die erstellte Simulation entspricht dabei gut den im Unterpunkt Das periodisch angetriebene Pendel dargestellten Resultaten.
Das Attraktordiagramm (Feigenbaum-Diagramm) wurde mithilfe des folgenden C++ Programms erstellt.
// Das periodisch angetriebenen Pendel (Übungsblatt 12) /* Beispiel eines schwingenden Systems aus dem Bereich der Mechanik * welches bei gewissen Parameterkonstellationen deterministisch chaotische Bewegungen zeigt * Berechnung der Loesung eines Systems von Differentialgleichungen * mittels Runge-Kutta Ordnung vier Verfahren * Verfahren zur Loesung der DGL ist in einer Klasse ausgelagert * Zeitentwicklung, t-Werte in [a,b] * Konstruktor mit neun Argumenten (Initialisierung der Instanzvariablen (m,l,beta,A,Omega), vier Argumente für dsolve) * Attraktordiagramm vieler Pendel mit unterschiedlichen Amplitudenwerten (Feigenbaum-Diagramm) * Ausgabe zum Plotten mittels Python Skript PythonPlot_GetriebPendel_attr.py: "./a.out > GetriebenesPendel_AttrDiag.dat" */ #include <iostream> // Standard Input- und Output Bibliothek in C, z.B. printf(...) #include <cmath> // Bibliothek für mathematisches (e-Funktion, Betrag, ...) #include <vector> // Vector-Container der Standardbibliothek #include "Pendel.hpp" // Header-Datei des physikalischen und mathematischen Pendels mit Reibung (Stokesscher Ansatz) using namespace std; // Benutze den Namensraum std // Hauptfunktion int main(){ double m = 1.0; // Masse des Pendels double l = 9.81; // Länge des Pendels double beta = 0.5; // Reibungskoeffizient unsigned int Anz_Pendel = 2000; // Anzahl der Pendel im Attraktordiagramm double Omega = 2.0/3; // Deklaration und Initialisierung der Frequenz Omega der ausseren periodisch Kraft unsigned int Anz_Punkte = 300000; // Anzahl der Punkte in die das t-Intervall aufgeteilt wird unsigned int Anz_Punkte_attr = 100; // Anzahl der Punkte im Attraktordiagramm (minus 70 Punkte fuer die Einschwingphase) double t_end = Anz_Punkte_attr * 2.0*M_PI/Omega; // Obergrenze des t-Intervalls [0,t_end] als Vielfaches der Zeitabstaende t_ni = 2*M_PI/Omega int i_schritt = Anz_Punkte/Anz_Punkte_attr; // Anzahl der Iterationen fuer einen Zeitabstand t_ni = 2*M_PI/Omega double Anf_A = 0.8; // Anfangswert der Amplitude A der ausseren periodischen Kraft im Attraktordiagramm double End_A = 2.5; // Endwert der Amplitude A der ausseren periodischen Kraft im Attraktordiagramm double dA = (End_A - Anf_A)/(Anz_Pendel-1); // Schrittweite dA der Amplitude A der ausseren periodischen Kraft im Attraktordiagramm vector<vector<double>> attr_wert(Anz_Pendel); // Deklaration einer double Vektor-Matrix zum speichern der Loesungen der Attraktorwerte der unterschiedlichen Pendel for (unsigned int n = 0; n < Anz_Pendel; ++n){ // Pendel-Konstruktor (Zeit-Intervall: [0,t_end], Anzahl der Zeit-Punkte: Anz_Punkte, Anfangsort und Geschwindigkeit: {0,0}, Amplitude A und Frequenz Omega der ausseren periodischen Kraft) Pendel_getrieb P_A = Pendel_getrieb(m,l,beta,Anf_A+n*dA,Omega,0,t_end,Anz_Punkte,{0,0}); // Konstruktor bilded eine Instanz der Klasse Pendel_getrieb P_A.solve(); // Methode der Runge-Kutta-Methode ausführen // Berechnung der Werte fuer das Attraktordiagramm (Winkelgeschwindigkeit in regelmaessigen Zeitabstaenden t_ni = ni * 2*M_PI/Omega) unsigned int ni = 70; // Deklaration des Integerwertes der Zeitwerte des Attraktordiagramms mit Einschwingphase (70 * 2*M_PI/Omega) vector<double> attr_wert_n; // Deklaration eines vector-Containers der Winkelgeschw. der Pendel-Loesungen zur Zeit t_ni attr_wert_n.push_back(Anf_A+n*dA); // attr_wert_n[0] ist jedoch die Amplitude A der ausseren periodischen Kraft while(ni <= Anz_Punkte_attr){ // while-Schleife ueber alle Zeitwerte des Attraktordiagramms attr_wert_n.push_back( P_A.ym[ni*i_schritt][1]); // Winkelgeschw. zur Zeit t_ni ni++; // Naechster Zeitwert des Attraktordiagramms } // Ende while-Schleife attr_wert[n] = attr_wert_n; // Fuellen der Vektor-Matrix der Attraktordiagramm-Werte des n-ten Pendels } // Ende der for-Schleife, Ende der Parallelisierung for(unsigned int n=0; n < Anz_Pendel; ++n){ // for-Schleife zur Terminalausgabe, unterschiedliche Pendel-Loesungen for(size_t i=0; i < attr_wert[n].size(); ++i){ // for-Schleife zur Terminalausgabe, unterschiedliche Pendel-Zeitwerte t_ni printf("%19.15f ",attr_wert[n][i]); // Ausgabe Winkelgeschw. des n-ten Pendels zur Zeit t_ni } // Ende for-Schleife, Pendel-Zeitwerte t_ni printf("\n"); } // Ende for-Schleife, unterschiedliche Pendel-Loesungen } // Ende der Hauptfunktion
Da die numerischen Rechnungen sehr zeitintensiv sind, wurde eine parallele OpenMP-Version des Programms erstellt (siehe GetriebenesPendel_attr_dia_Klasse_omp.cpp). Das im Unterpunkt Das periodisch angetriebene Pendel dargestellte Attraktordiagramm wurde mittels dieser parallelen C++-Version und des Python-Skriptes PythonPlot_GetriebPendel_attr.py reproduziert (siehe Abbildung unten rechts). Zusätzlich wurde ein weiteres Attraktordiagramm erzeugt, welches einen größeren Amplitudenbereich visualisiert ($A \in [0.8 , 2.5]$, siehe Abbildung unten rechts).
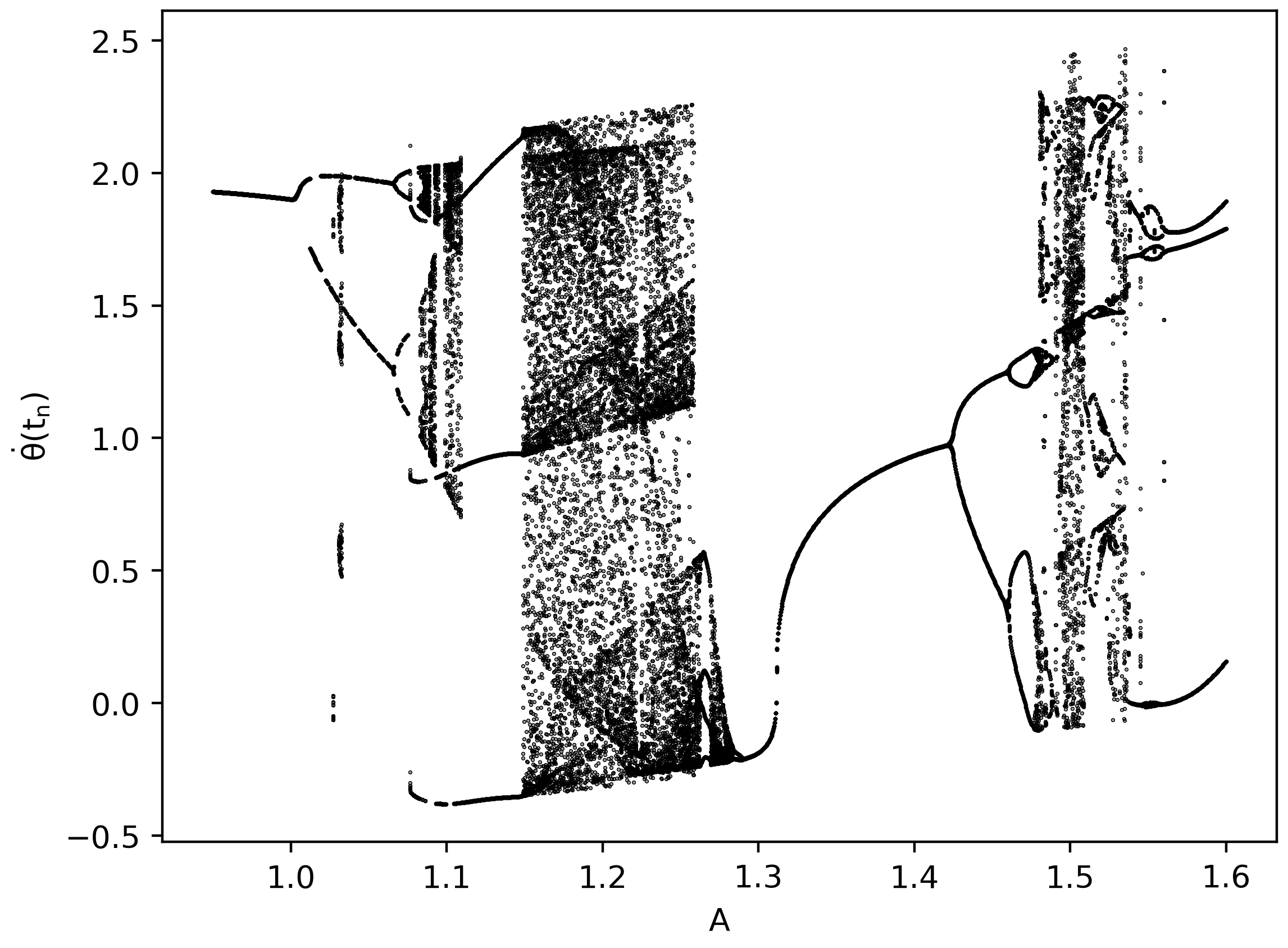
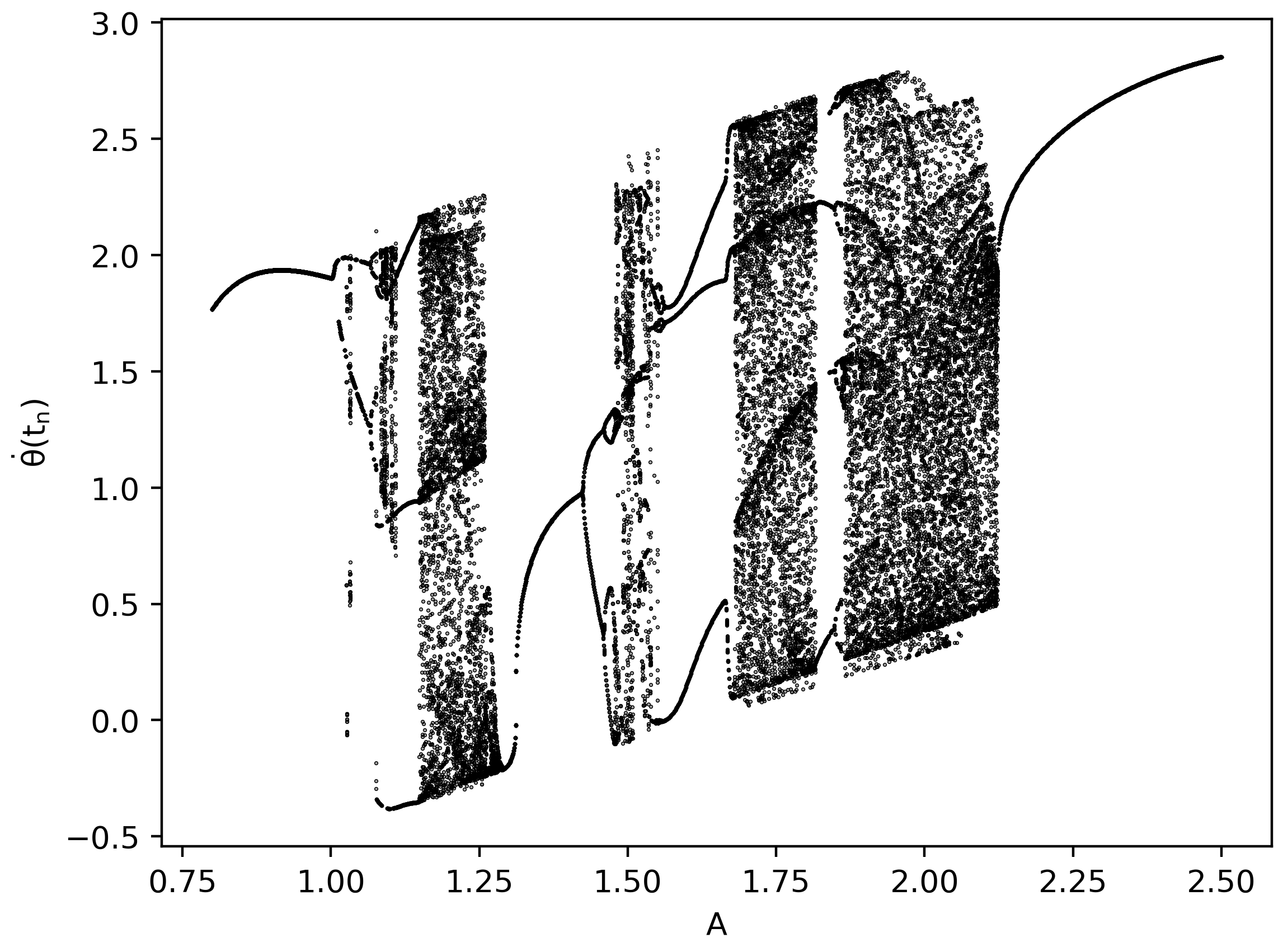
Des Weiteren wurden zwei Attraktordiagramme erstellt, bei denen jeweils einer der Parameter des Systems ($\beta$ bzw. $\Omega$) verändert wurden. Die Abbildung unten links zeigt eine Vergrößerung des Reibungsparameters ($\beta = 0.65$) und die Abbildung unten rechts zeigt eine Verringerung der Frequenz der antreibenden periodischen Kraft ($\Omega = \frac{2}{3.5}$).
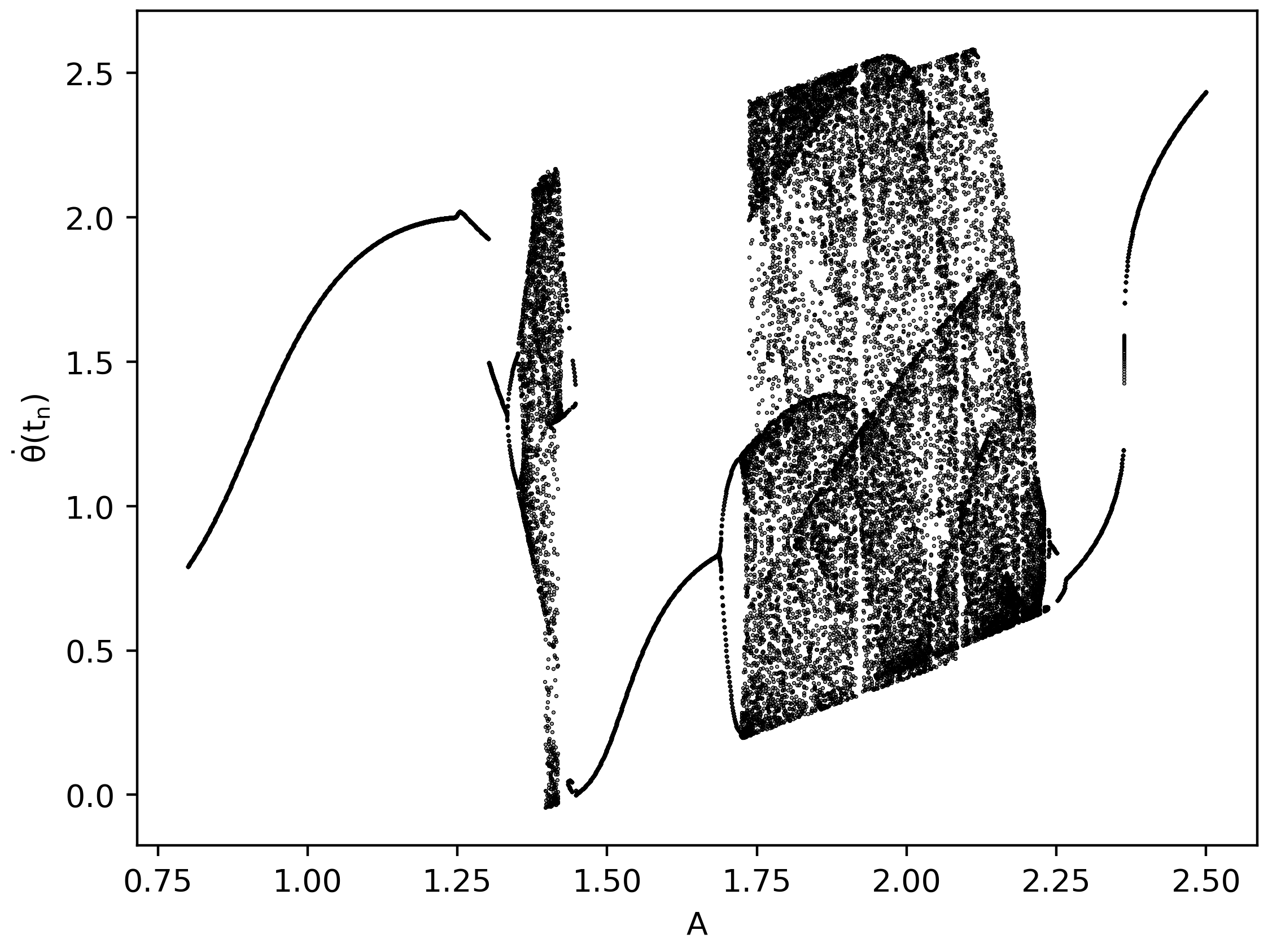
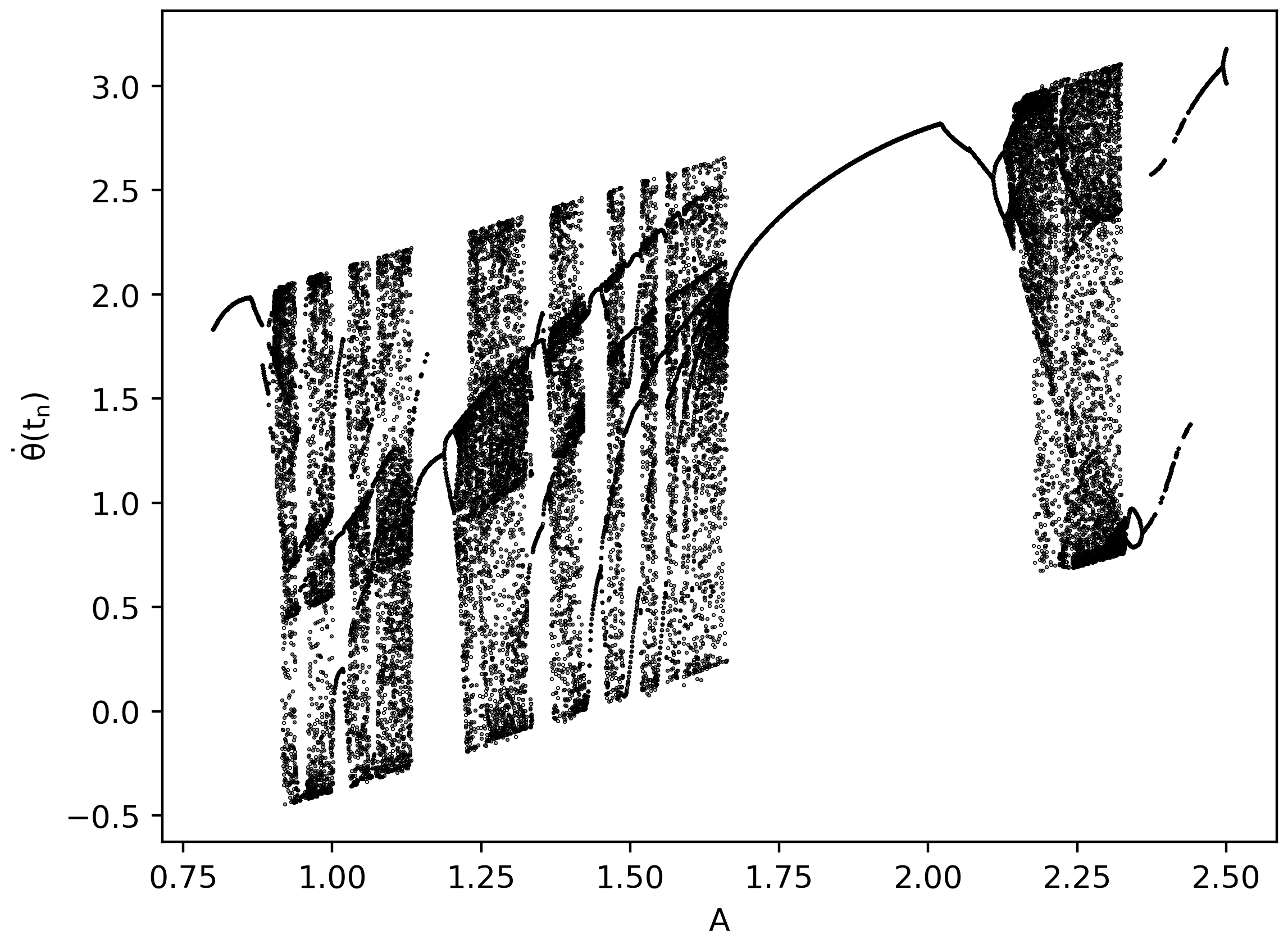
Anhand der erstellten Feigenbaum-Diagramme erkennt man gut, dass die Struktur und die Abfolge von regulären und chaotischen Bereichen stark von den Parametern des Systems abhängt.