Übungsblatt Nr. 7
Aufgabe 1 (10 Punkte)
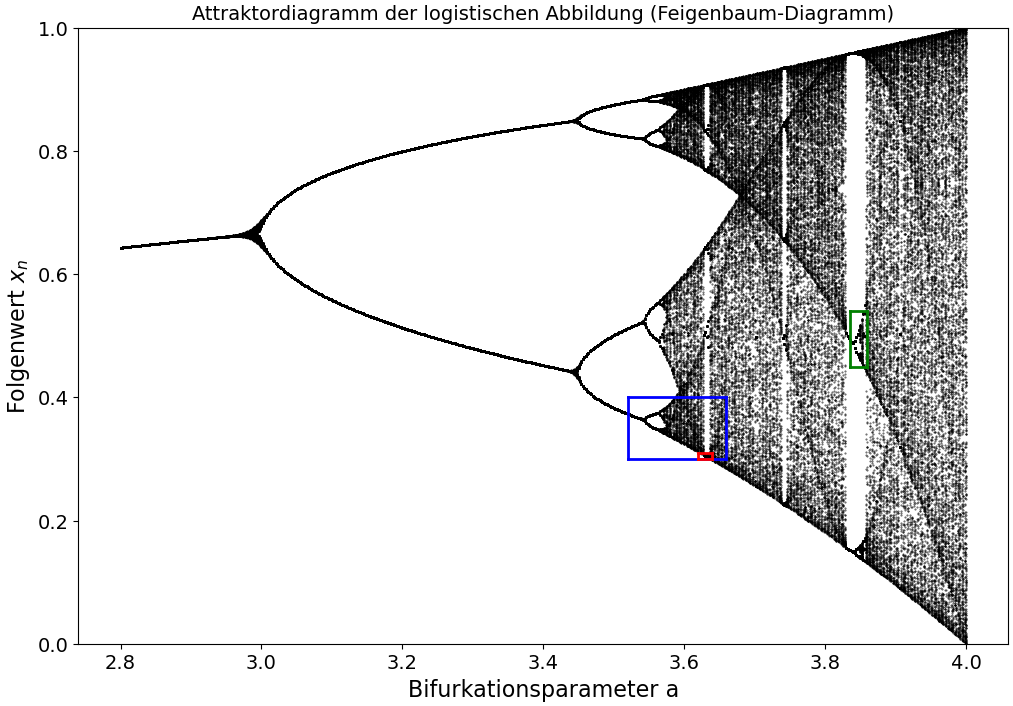
In der Vorlesung 3, im Unterkapitel Anwendungsbeispiel: Folgen und Reihen, hatten wir die logistische Abbildung besprochen. Die logistische Gleichung ist die wohl meist betrachtete diskrete Gleichung im Zusammenhang mit chaotischem Verhalten. Um einen globalen Überblick über das Verhalten dieses teils-chaotischen Systems zu erhalten, erstellten wir mittels des C++ Programms Logi_AttrDiag.cpp ein Attraktordiagramm (Feigenbaum-Diagramm, siehe nebenstehende Abbildung). Die Abfolge von regulären und chaotischen Bereichen werden hierbei visualisiert, indem man die Folgenwerte als Funktion eines Systemparameters (hier der Bifurkationsparameter $a$) darstellt. Betrachtet man das nebenstehende Feigenbaum-Diagramm, so erkennt man, dass inmitten der chaotischen Bereiche einige Inseln der Ordnung auftreten. Vergrößert man die entsprechenden Bereiche (siehe blaues, grünes und rotes Rechteck in der nebenstehenden Abbildung), so zeigen sich weitere kleine Heugabel-Verzweigungen, bei denen eine Periodenverdopplung der periodischen Lösung auftritt und die ihrerseits wiederum den Weg in das Chaos aufzeigen. In diesem Zusammenhang spricht man von Selbstähnlichkeit und Skaleninvarianz der logistischen Abbildung.
Lagern Sie den Kern-Algorithmus der Berechnung des Feigenbaum-Diagramms in einer C++ Klasse aus. Mittels der Argumentenliste des Konstruktors der Klasse sollte man dabei einfach den gewünschten Visualisierungsbereich des Bifurkationsparameter $a$ auswählen können und gegebenenfalls Abänderungen an anderen Parametern, z.B. der Anzahl der dargestellten Folgenglieder $N$, machen können. Überprüfen Sie ihr Programm, indem Sie ihre Berechnungen mit denen im Unterpunkt Anwendungsbeispiel: Folgen und Reihen dargestellten Ergebnissen vergleichen ($a \in [2.8, 4.0]$ und $x_n \in [0, 1]$). Erstellen Sie hierzu ebenfalls ein Bild des Feigenbaum-Diagramms mittels des Python-Skripts PythonPlot_Logi_AttrDiag.py. Stellen Sie zusätzlich die in der nebenstehenden Abbildung gekennzeichneten Zoom-Bereiche des Feigenbaum-Diagramms dar ( Zoom 1 (blau): $a \in [3.52, 3.66]$ und $x_n \in [0.3, 0.4] \quad$ , $\quad$ Zoom 2 (rot): $a \in [3.62, 3.64]$ und $x_n \in [0.3, 0.31] \quad$ und $\quad$ Zoom 3 (grün): $a \in [3.835, 3.86]$ und $x_n \in [0.45, 0.54] $ ).
Aufgabe 2 (10 Punkte)
Diese Aufgabe ist angelehnt an das Kapitel 23 "Der gedämpfte harmonische Oszillator" des Buches von Prof. Walter Greiner, Mechanik (Teil 1) [5. Auflage, 1989, siehe Seite 226- 237]. Siehe auch Vorlesungsskript von Prof. Rischke auf Seite 117- 126 http://itp.uni-frankfurt.de/~drischke/Skript_MI_WiSe2016-2017.pdf ). Wir betrachten im Folgenden den gedämpften harmonischen Oszillator am Beispiel eines reibungsfrei gelagerten Wagens (Masse=$M$) auf den eine Rückstellkraft einwirkt (die proportional zu seiner Auslenkung $x$ ist (Proportionalitätskonstante $k$)), wobei zusätzlich eine geschwindigkeitsabhängige Reibungskraft auf den Wagen einwirkt (z.B. verursacht durch den auf den Wagen einwirkende Luftwiderstand, Stokesscher Ansatz: Proportionalitätskonstante $\alpha$). Aufgrund der Rückstellkraft, besitzt das zugrundeliegende Potential $V(x)$ die Form einer Parabel $V(x)=\frac{k \, x^2}{2}$. Die zeitliche Entwicklung des linearen harmonischen Oszillators mit Dämpfung wird mittels der folgenden Differentialgleichung zweiter Ordnung beschrieben (wir setzen $\omega_0^2=\frac{k}{M}$ und $\beta = \frac{\alpha}{2M}$): $$ \begin{equation} \ddot{x}(t) = - \omega_0^2 \, x(t) - 2 \beta \, \dot{x}(t) \end{equation} $$ Die Anfangsbedingungen seien zunächst noch allgemein gehalten: $x(0) = \alpha_1 \,\, , \,\, \dot{x}(0) = \alpha_2$. Bestimmen Sie die allgemeine Lösung der Differentialgleichung mittels eines eigenen Jupyter Notebooks. Geben Sie dann die spezielle Lösung der Differentialgleichung bei festgelegten Parameterwerten ($\omega_0^2=3$ und $\beta = 0.25$) und Anfangsbedingungen ($\alpha_1 = 0$ und $\alpha_2 = 40$) an und visualisieren Sie diese in einem x-t Diagramm. An welchem Ort befindet sich der Wagen zur Zeit $t=10$ ( $x(10)$ )?
Die Musterlösung der Aufgaben des Übungsblattes Nr. 7 finden Sie unter dem folgenden Link:
Musterlösung Übungsblatt Nr. 7