Musterlösung zum Übungsblatt Nr. 7
Musterlösung zur Aufgabe 1 (10 Punkte)
Im folgenden C++ Programm wurde der Kern-Algorithmus zur Berechnung des Feigenbaum-Diagramms der logistischen Abbildung (näheres siehe Vorlesung 3, Unterkapitel Anwendungsbeispiel: Folgen und Reihen) in einer C++ Klasse ausgelagert.
// Musterlösung der Aufgabe 1 des Übungsblattes Nr.7 /* C++ Klasse des Attraktordiagramms der logistischen Abbildung (Feigenbaum-Diagramm) * Ausgabe zum Plotten (Gnuplot oder Python) mittels: "./a.out > Logi_AttrDiag_Klasse.dat" */ #include <iostream> // Ein- und Ausgabebibliothek class LogiDiag { // Private Instanzvariablen double a_start; // Anfangswert des Bifurkationsparameters (Verzweigungsparameter) a in (1,4] double a_end; // Endwert des Bifurkationsparameters a in (1,4] int N_a; // Anzahl der a-Werte double x0; // Anfangswert der Folge als double Zahl x0 in [0,1] int N; // Anzahl der Folgenglieder int N_skip; // Anzahl der Folgenglieder die man nicht im Terminal ausgibt (transienter Einschwingvorgang) // Öffentliche Bereich der Klasse public: // Konstruktor mit Standardinitialisierungen LogiDiag(double a_start = 2.8, double a_end = 4.0, int N_a = 600, double x0 = 0.1, int N = 400, int N_skip = 100) : a_start{a_start}, a_end{a_end}, N_a{N_a}, x0{x0}, N{N}, N_skip{N_skip} {} // Öffentliche Methode zur Terminalausgabe des Feigenbaum-Diagramms void erzeuge_feigenbaum() { double da = (a_end - a_start)/N_a; // Schrittweite des Bifurkationsparameters printf("# 0: Verzweigungsparameter a \n# 1...: Werte der Folge x_n \n"); // Beschreibung der ausgegebenen Groessen for(int i=0; i<=N_a; ++i){ // for-Schleife ueber die Werte des Verzweigungsparameter double a = a_start + i*da; // Aktueller a-Wert printf("%8.4f ", a); // Ausgabe des Verzweigungsparameters double x = x0; // Initialisierung Anfangswert x_0 in [0,1] for(int n=0; n<=N; ++n){ // for-Schleife ueber die Folgenwerte if( n > N_skip ){ // Nur Folgenwerte nach der transienten Phase ausgeben printf("%20.15f ", x); // Ausgabe des Folgenwertes } // Ende if x = a*x*(1 - x); // Math. Modell der logistischen Abbildung } // Ende der for-Schleife ueber die Folgenwerte printf("\n"); // Ausgabe neue Zeile } // Ende for-Schleife ueber die Werte des Verzweigungsparameters } // Ende der Ausgabenmethode des Feigenbaum-Diagramms }; // Ende der Klasse // Hauptfunktion int main(){ // Erstellen einer Instanz der Klasse mit Standardparametern (ursprüngliches Feigenbaum-Diagramm) //LogiDiag feigen_standard; //feigen_standard.erzeuge_feigenbaum(); // Erstellen einer Instanz der Klasse mit Parametern des ersten Zooms //LogiDiag feigen_zoom1 = LogiDiag(3.52, 3.66); //feigen_zoom1.erzeuge_feigenbaum(); // Erstellen einer Instanz der Klasse mit Parametern des zweiten Zooms //LogiDiag feigen_zoom2 = LogiDiag(3.62, 3.64,1500,0.1,1000,300); //feigen_zoom2.erzeuge_feigenbaum(); // Erstellen einer Instanz der Klasse mit Parametern des dritten Zooms LogiDiag feigen_zoom3 = LogiDiag(3.835, 3.86,1000,0.1,700,300); feigen_zoom3.erzeuge_feigenbaum(); }
Mittels der Argumentenliste des Konstruktors werden die sechs privaten Instanzvariablen der Klasse mit den Standardwerten initialisiert. Neben dem Anfangs- und Endwert des Bifurkationsparameter $a$ (double a_start und double a_end) und der Anzahl unterschiedlicher a-Werte (int N_a) werden noch drei weitere, die Visualisierung bestimmende Größen, initialisiert (double x0, int N und int N_skip). Die öffentliche Methode 'void erzeuge_feigenbaum() { ... }' stellt die eigentliche Terminalausgabe des Feigenbaum-Diagramms dar. Um die anfängliche, transiente Phase nicht zu betrachten wurden hierbei nur Folgenglieder ausgegeben, deren Folgenindex 'n' größer als 'N_skip' ist.
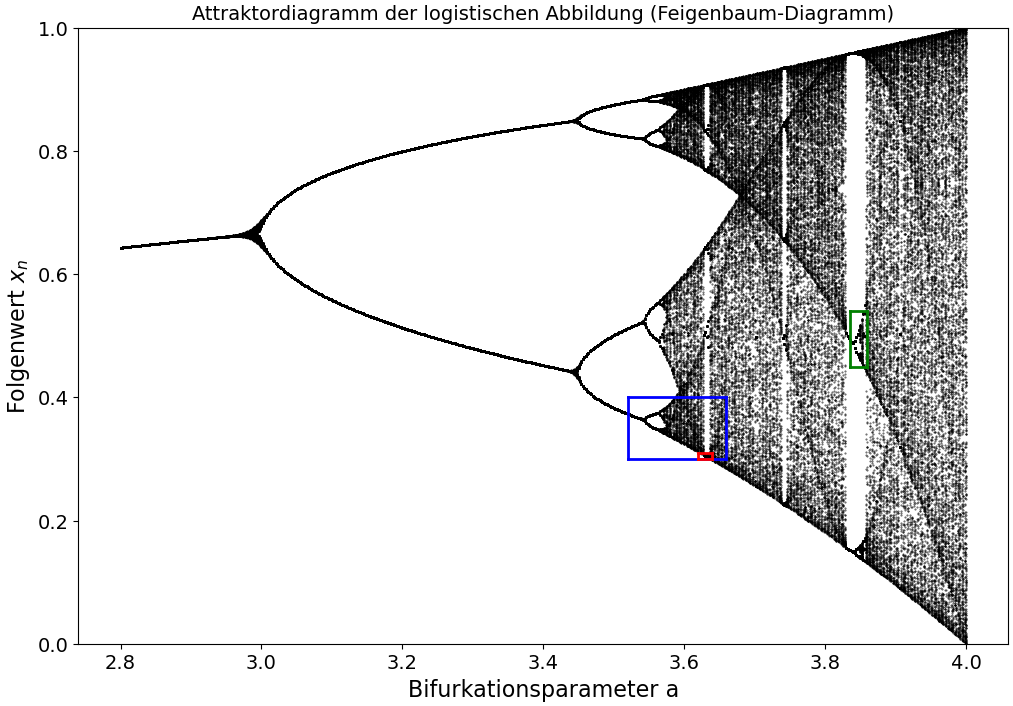
Um die verschiedenen Bereiche des Feigenbaum-Diagramms darzustellen, wurden nun in der Hauptfunktion nacheinander unterschiedliche Instanzen der Klasse gebildet. Zunächst wurden die Berechnungen des Programms mit den ursprünglichen Ergebnissen des im Unterpunkt Anwendungsbeispiel: Folgen und Reihen dargestellten Programms verglichen ($a \in [2.8, 4.0]$ und $x_n \in [0, 1]$). Hierbei wurde mittels des Standard-Konstruktors 'LogiDiag feigen_standard;' eine Instanz der Klasse erzeugt und danach die Methode 'feigen_standard.erzeuge_feigenbaum();' verwendet. Die Ergebnisse wurden dann mittels './a.out > Logi_AttrDiag_Klasse.dat' in eine Datei umgeleitet und mit dem Python Skript PythonPlot_Logi_AttrDiag_Klasse.py visualisiert (siehe Abbildung unten links).
Um die Selbstähnlichkeit und Skaleninvarianz der logistischen Abbildung zu verdeutlichen wurden nun gewisse Bereiche des Feigenbaum-Diagramms vergrößert (siehe blaues, grünes und rotes Rechteck in der linken unteren Abbildung). Zunächst betrachteten wir das blaue Rechteck (Zoom 1: $a \in [3.52, 3.66]$ und $x_n \in [0.3, 0.4]$), indem wir den $a$-Bereich durch die Instanzbildung 'LogiDiag feigen_zoom1 = LogiDiag(3.52, 3.66);' verkleinerten und die anderen Instanzvariablen auf ihren Standardwerten beließen. Die Ergebnisse wurden wieder mittels './a.out > Logi_AttrDiag_Klasse.dat' in eine Datei umgeleitet und mit dem Python Skript PythonPlot_Logi_AttrDiag_Klasse.py visualisiert (siehe Abbildung unten rechts). Die y-Achse der Abbildung ($x_n \in [0.3, 0.4]$) wurde dabei mittels des Python-Skriptes beschränkt.
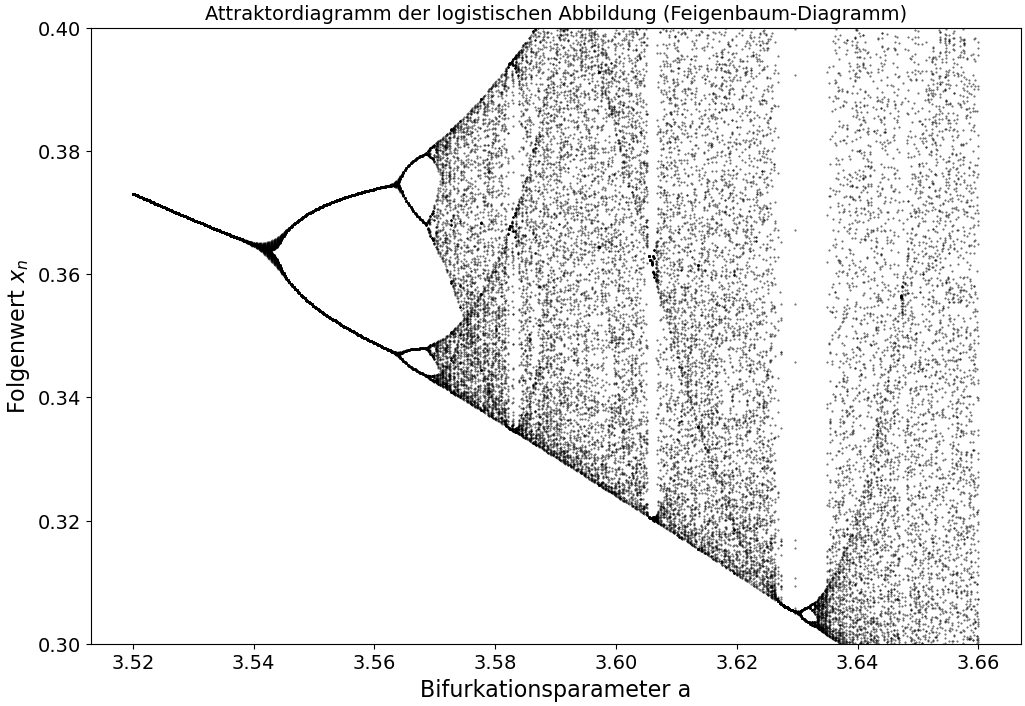
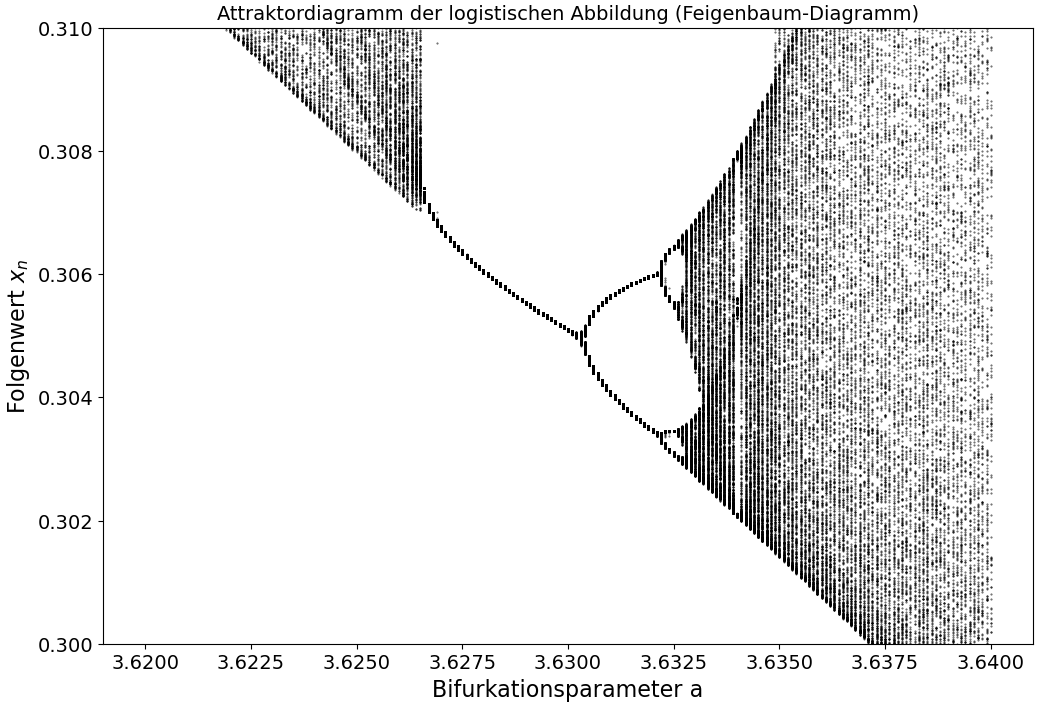
Als nächstes betrachteten wir uns den Visualisierungsbereich des roten kleinen Rechtecks (Zoom 2: $a \in [3.62, 3.64]$ und $x_n \in [0.3, 0.31]$). Da es sich dabei um einen sehr kleinen $a$-Bereich handelte, mussten wir einige Standardwerte der Instanzvariablen abändern und benutzten den Konstruktor mit allen seinen sechs Argumenten: 'LogiDiag feigen_zoom2 = LogiDiag(3.62, 3.64,1500,0.1,1000,300);'. Die Ergebnisse sind in der unteren rechten Abbildung dargestellt.
Am Ende benutzen wir dann den Konstruktor 'LogiDiag feigen_zoom3 = LogiDiag(3.835, 3.86,1000,0.1,700,300);' um den Bereich des grünen Rechtecks darzustellen (Zoom 3 : $a \in [3.835, 3.86]$ und $x_n \in [0.45, 0.54]$, siehe Abbildung unten links).
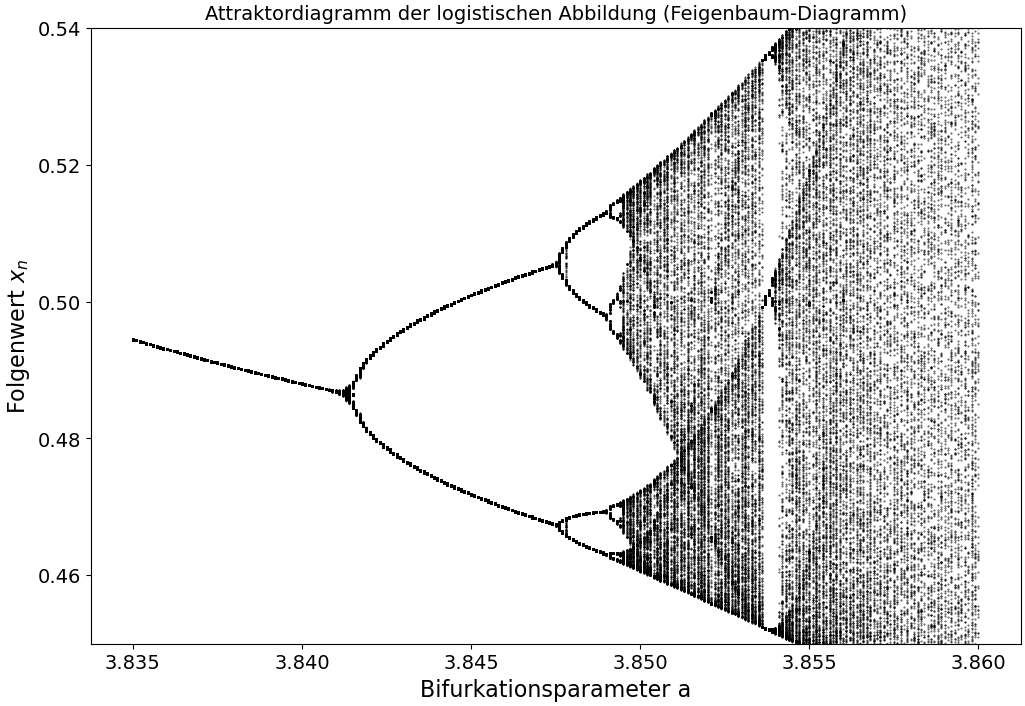
In den dargestellten Abbildungen wurde somit die Selbstähnlichkeit und Skaleninvarianz der logistischen Gleichung gut verdeutlicht.
Musterlösung zur Aufgabe 2 (10 Punkte)
Diese Aufgabe ist angelehnt an das Kapitel 23 "Der gedämpfte harmonische Oszillator" des Buches von Prof. Walter Greiner, Mechanik (Teil 1) [5. Auflage, 1989, siehe Seite 226- 237]. Siehe auch Vorlesungsskript von Prof. Rischke auf Seite 117- 126 http://itp.uni-frankfurt.de/~drischke/Skript_MI_WiSe2016-2017.pdf ). Wir betrachten im Folgenden den gedämpften harmonischen Oszillator am Beispiel eines reibungsfrei gelagerten Wagens (Masse=$M$) auf den eine Rückstellkraft einwirkt (die proportional zu seiner Auslenkung $x$ ist (Proportionalitätskonstante $k$)), wobei zusätzlich eine geschwindigkeitsabhängige Reibungskraft auf den Wagen einwirkt (z.B. verursacht durch den auf den Wagen einwirkende Luftwiderstand, Stokesscher Ansatz: Proportionalitätskonstante $\alpha$). Aufgrund der Rückstellkraft, besitzt das zugrundeliegende Potential $V(x)$ die Form einer Parabel $V(x)=\frac{k \, x^2}{2}$. Die Differentialgleichung des linearen harmonischen Oszillators mit Dämpfung wird mittels der folgenden Differentialgleichung zweiter Ordnung beschrieben (wir setzen $\omega_0^2=\frac{k}{M}$ und $\beta = \frac{\alpha}{2M}$): $$ \begin{equation} \ddot{x}(t) = - \omega_0^2 \, x(t) - 2 \beta \, \dot{x}(t) \end{equation} $$ Die Anfangsbedingungen seien zunächst noch allgemein gehalten: $x(0) = \alpha_1 \,\, , \,\, \dot{x}(0) = \alpha_2$. Bestimmen Sie die allgemeine Lösung der Differentialgleichung mittels eines eigenen Jupyter Notebooks. Geben Sie dann die spezielle Lösung der Differentialgleichung bei festgelegten Parameterwerten ($\omega_0^2=3$ und $\beta = 0.25$) und Anfangsbedingungen ($\alpha_1 = 0$ und $\alpha_2 = 40$) an und visualisieren Sie diese in einem x-t Diagramm. An welchem Ort befindet sich der Wagen zur Zeit $t=10$ ( $x(10)$ )?
Das nebenstehende Jupyter Notebook A7_2.ipynb (View Notebook, Download Notebook) stellt die Musterlösung der Aufgabe dar.
