 |
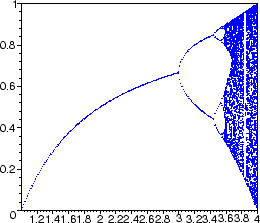
Feigenbaum Diagramm: Periodenverdopplung der logistischen
Abbildung
für kritische Werte r(k) des Kontrollparameters r. |
 |
Feigenbaum Diagramm: Periodenverdopplung der logistischen
Abbildung
für kritische Werte r(k) des Kontrollparameters r. |
|
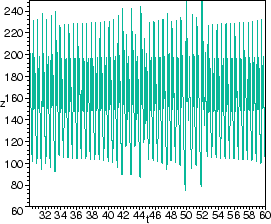
Intermittenz Pfad zum Chaos: Lösung z(t) des Lorenz Modells für r=166.4 |