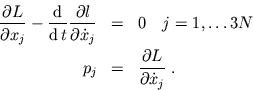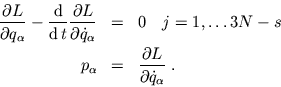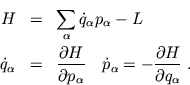8 Einführung in die analytische Mechanik

Ausgangspunkt einer Verallgemeinerung der theoretischen Beschreibung mechanischer Systeme ist das Hamilton Prinzip der minimalen Wirkung:
Von allen möglichen Pfaden zwischen zwei Punkten wird die Dynamik eines Systems innerhalb eines vorgegebenen Zeitintervalls durch denjenigen Pfad beschrieben, für den das Zeitintegral über die Differenz aus kinetischer und potentieller Energie minimal ist.
Mathematisch bedeutet dies

wobei 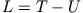die Lagrange Funktion bedeutet und 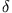die Variation des Zeitintegrals bezüglich verschiedener Bahnkurven des mechanischen Systems darstellt. Das Wirkungsprinzip ist so formuliert, dass sich aus ihm die Newton'schen Bewegungsgleichungen ableiten.In kartesischen Koordinaten erhält man aus der Extremalbedingung die Lagrange Gleichungen

Die Lagrange Gleichungen sind forminvariant bezüglich generalisierter Koordinaten. Diese verallgemeinerten Koordinaten 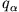enthalten Symmetrien und 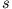Zwangsbedingungen, die die Zahl der Freiheitsgrade 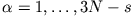reduzieren, d.h. bezogen auf die generalisierten Koordinaten gilt

Sind alle Zwangsbedingungen holonom und skleronom, sind die generalisierten Koordinaten nur abhängig von den kartesischen Koordinaten (also unabhängig von Geschwindigkeit und Zeit)

Ist die Lagrange Funktion von einer bestimmten generalisierten Koordinate 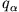(zyklische Koordinate) unabhängig, repräsentiert der zugehörige generalisierte Impuls 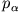eine Erhaltungsgröße

Äquivalent zu den Bewegungsgleichungen von Lagrange sind die Hamilton'schen (kanonischen) Bewegungsgleichungen (H: Hamilton Funktion)

Für zwei stetige Funktionen der generalisierten Koordinaten und Impulse 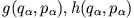definiert man die Poissonklammern (Vertauschungsrelationen)

Sie erlauben eine elegante Formulierung von Erhaltungsgrößen, da

Ist 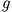nicht explizit zeitabhängig und vertauscht mit der Hamilton Funktion, so ist 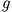eine Erhaltungsgröße des mechanischen Systems.
Insbesondere ist 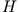eine Erhaltungsgröße (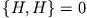). 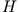ist identisch mit der totalen mechanischen Energie (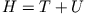), falls alle Zwangsbedingungen holonom und skleronom sind. Die kanonischen Bewegungsgleichungen lassen sich elegant mit Hilfe der Vertauschungsrelationen formulieren

Die generalisierten Impulse und Koordinaten erfüllen die Vertauschungsrelationen