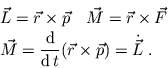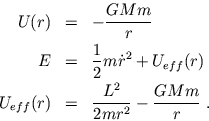Ein Massenpunkt besitzt bezogen auf ein Koordinatensystem
einen Drehimpuls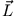 
und ein Drehmoment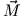 
Die Arbeit, die aufgewandt werden muss, um einen Massenpunkt zwischen
zwei Orten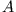 
und 
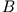in einem Kraftfeld 
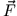entlang einer Trajektorie 
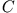zu bewegen, ist
Für Zentralkräfte
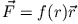ist die Arbeit unabhängig
vom gewählten Weg zwischen den Endpunkten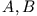 
. Analog zu eindimensionalen
Bewegungsformen gilt dann
Dabei ist die potentielle Energie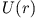 
von der Form, dass
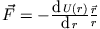. Der Energiesatz
lautet
Für ein Gravitationsfeld gilt in Kugelkoordinaten
Das effektive Potential setzt sich zusammen aus dem Zentrifugalpotential
(1. Term) und dem Gravitationspotential (2. Term). Der Wert der
totalen konstanten Energie bestimmt die Form der Bahn des Massenpunktes
im Zentralkraftfeld: (i)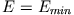 
: Kreisbahn, (ii)
:
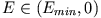Ellipsenbahn mit dem Kraftzentrum in einem Brennpunkt der Ellipse,
(iii)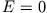 
: Parabelbahn, (iv) 
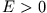: Hyperbelbahn. Ist die Gesamtenergie
negativ, so spricht man von gebundenen Bahnen, sonst von ungebundenen
Bahnen. Diese Aussage über die möglichen Bahnformen entspricht
dem 1. Kepler Gesetz. Das 2. Kepler Gesetz besagt, dass der Drehimpuls
in einem Zentralkraftfeld eine Erhaltungsgröße ist und das
3. Kepler Gesetz fordert, dass für gebundene Bahnen das
Quadrat der Umlaufzeit der 3. Potenz der Halbachse proportional ist.
H.J. Lüdde
