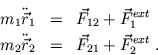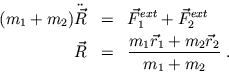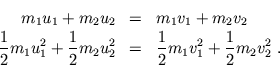4. Bewegung zweier Körper

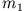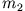Ein System von zwei Massenpunkten und spührt die gegenseitigen inneren Kräfte 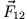und 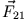, sowie eventuelle äußere Kräfte ( 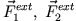). Die Bewegungsgleichung lautet

Addition der beiden Gleichungen ergibt

Der Ortsvektor 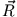definiert den Schwerpunkt des Systems. Verschwinden die äußeren Kräfte (abgeschlossene Systeme), so ist der Impuls des Schwerpunktes eine Erhaltungsgröße. Subtraktion der beiden Gleichungen ergibt

Dabei nennt man 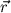die Relativkoordinate des Systems. Führt man die reduzierte Masse ein

so erhält man für ein System ohne äußere Kräfte

Die Relativbewegung beschreibt also ein effektives Einteilchen- Problem: die Bewegung eines effektiven Teilchens der Masse 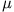im Zentralfeld 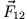. Elastische Stöße zwischen zwei Massenpunkten eines abgeschlossenen Systems sind charakterisiert durch Impuls- und Energieerhaltung

Dabei bezeichnet 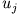die Geschwindigkeiten der Massenpunkte vor dem Stoß und 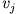diejenigen nach dem Stoß.