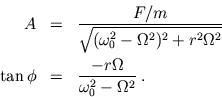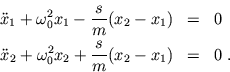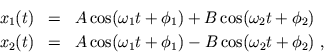3. Oszillatoren
Die Bewegungsgleichung eines getriebenen, gedämpften harmonischen
(lineare Rückstellkraft) Oszillators ist gegeben durch
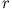 entspricht der Stärke der Dämpfung und
entspricht der Stärke der Dämpfung und 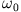 ist die
Eigenfrequenz des freien Oszillators. Die allgemeine Lösung der
Bewegungsgleichung - sie setzt sich zusammen aus der allgemeinen
Lösung des ungetriebenen Oszillators und einer speziellen Lösung
des getriebenen Systems - lautet
ist die
Eigenfrequenz des freien Oszillators. Die allgemeine Lösung der
Bewegungsgleichung - sie setzt sich zusammen aus der allgemeinen
Lösung des ungetriebenen Oszillators und einer speziellen Lösung
des getriebenen Systems - lautet
wobei für die Frequenz des gedämpften Oszillators gilt
Die Integrationskonstanten der allgemeinen Lösung 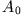 (Amplitude)
und
(Amplitude)
und 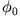 (Phasenwinkel) bestimmen sich durch die Anfangsbedingungen
(Phasenwinkel) bestimmen sich durch die Anfangsbedingungen
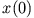 und
und 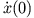 . Die Lösung zerfällt in zwei Bewegungsformen:
(i) der Einschwingvorgang (1. Term) wird bestimmt durch das
Wechselspiel zwischen Rückstellkraft und externer Antriebskraft,
gedämpft durch den Reibungsterm (ii) die asymptotische Lösung
(2. Term) oszilliert synchron zur harmonischen Antriebskraft
mit einer Phasenverschiebung. Im Phasenraum zeigt sich die typische
Form einer Grenzkreislösung (limit cycle) mit der asymptotischen
Lösung als Grenzkreis.
. Die Lösung zerfällt in zwei Bewegungsformen:
(i) der Einschwingvorgang (1. Term) wird bestimmt durch das
Wechselspiel zwischen Rückstellkraft und externer Antriebskraft,
gedämpft durch den Reibungsterm (ii) die asymptotische Lösung
(2. Term) oszilliert synchron zur harmonischen Antriebskraft
mit einer Phasenverschiebung. Im Phasenraum zeigt sich die typische
Form einer Grenzkreislösung (limit cycle) mit der asymptotischen
Lösung als Grenzkreis.
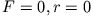 : der Massenpunkt oszilliert mit seiner Eigenfrequenz
: der Massenpunkt oszilliert mit seiner Eigenfrequenz 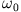 und konstanter Amplitude
und konstanter Amplitude 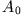 . Die gespeicherte mechanische Energie
beträgt (k: Federkonstante)
. Die gespeicherte mechanische Energie
beträgt (k: Federkonstante)
Die Phasenraumlösung enspricht einer Ellipse.
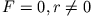 : der freie, gedämpfte harmonische Oszillator ist
gekennzeichnet durch drei Bewegungsformen:
: der freie, gedämpfte harmonische Oszillator ist
gekennzeichnet durch drei Bewegungsformen:
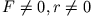 : die Lösung beginnt mit einem komplizierten Einschwingvorgang
der abhängig von der Dämpfung in einen asymptotischen Grenzkreiszustand
übergeht. Amplitude und Phase der asymptotischen Lösung ergeben sich
aus
: die Lösung beginnt mit einem komplizierten Einschwingvorgang
der abhängig von der Dämpfung in einen asymptotischen Grenzkreiszustand
übergeht. Amplitude und Phase der asymptotischen Lösung ergeben sich
aus
Resonanz erhält man, wenn der Nenner im Ausdruck für die Amplitude
minimal wird (setze 1. Ableitung des Nenners gleich 0)
Gekoppelte Schwingungen identischer Oszillatoren, die über eine
Feder der Federkonstanten 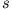 verbunden sind, lassen sich durch
folgende Bewegungsgleichungen beschreiben
verbunden sind, lassen sich durch
folgende Bewegungsgleichungen beschreiben
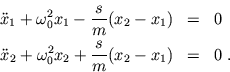
Die Lösung dieses ungedämpften Systems ist
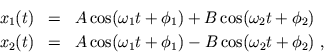
mit den Frequenzen
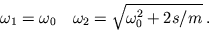
Die Bewegung ist generell eine Überlagerung aus zwei Normalschwingungen:
(i) Schwingung beider Massen in Phase mit der Frequenz 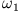 (ii) Schwingung beider Massen in Gegenphase mit der Frequenz
(ii) Schwingung beider Massen in Gegenphase mit der Frequenz 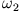 .
.
H.J. Lüdde