8.3.2 Bewegung eines Satelliten im System Erde-Mond

An diesem Beispiel wollen wir die Behandlung des eingeschränkten Dreikörperproblems etwas näher betrachten. Die Aufgabe wird sein u.a. eine Rakete auf einer ballistischen Flugbahn von der Erde zum Mond zu bringen und wieder zurück zur Erde.

Abbildung 8.10: Raumfestes Schwerpunktsystem

Das Raumschiff bewegt sich also im Gravitationsfeld von Erde und Mond. Erde und Mond bewegen sich in guter Näherung auf Kreisbahnen um den gemeinsamen Schwerpunkt. Störungen von Sonne und Planeten schließen wir aus und die Masse des Raumschiffs ist zu klein, um Himmelskörper zu beeinflussen. Das ist also das Kennzeichen eines eingeschränkten Dreikörperproblems: ein Körper mit geringer Masse bewegt sich im zeitabhängigen Potential zweier massereicher Körper. 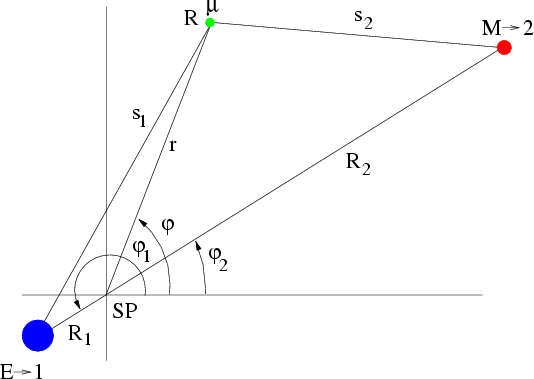Da keine äußeren Kräfte auf das System Erde-Mond-Raumschiff wirken, wird sich das Raumschiff bei entsprechender Anfangsbedingung in der Ebene der Mond-Erde Bahn bewegen. D.h. wir müssen ein zweidimensionales Anfangswertproblem lösen. Statt in kartesischen Koordinaten, wollen wir das Problem in System angepaßten Koordinaten lösen: ebene Polarkoordinaten. Wir müssen zunächst alle Koordinaten bezüglich des raumfesten Schwerpunktsystems ausdücken ( ist der als konstant angenommene Abstand zwischen Erde und Mond)

Tabelle 8.1: Koordinaten im eingeschränkten Dreikörperproblem

Erde	; ( )
Mond	; ( ),
Raumschiff	; (, )
Geschwindigkeit des Raumschiffs	,

Die Masse des Raumschiffs ist und wir können jetzt die Lagrange-Funktion bestimmen

Aus der Lagrange-Funktion erhalten wir die generalisierten Impulse

und somit die Hamilton-Funktion

Da das System als Zentralkraftproblem konservativ ist, also keine z.B. geschwindigkeits abhängigen Potentiale enthält (z.B. Reibung), ist die Hamilton-Funktion identisch mit der Gesamtenergie. Bezüglich der generalisierten Impulse gilt

und man erhält die Hamilton-Gleichungen

für die Bewegung des Raumschiffes in dem durch die Bewegung von Erde und Mond zeitabhängigen Potential. Diese Bewegungsgleichungen müssen numerisch gelöst werden, was Sie mit Hilfe dieses Applets durchspielen können. (Zur Orientierung öffnen Sie bitte das Hilfe Fenster nach dem Start des Applets. Sie erhalten darin Hinweise zur Steuerung des Programmes.)

Interessante Fragen sind z.B.

a)

Untersuche die Störung erdferner Satellitenbahnen durch das Gravitationsfeld des Mondes.

b)

Bestimme die Anfangsbedingung für einen ballistischen Flug zum Mond mit Rückkehr zur Erde.

Literatur:
E.W. Schmid, G. Spitz, W. Lösch: Theoretische Physik mit dem PC, Springer, 1987.