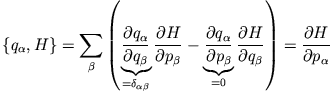Betrachte zwei stetige Funktionen der generalisierten Koordinaten und Impulse
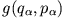und
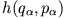. Die Poissonklammer dieser Funktionen ist definiert durch
Im allgemeinen verschwindet die Poissonklammer nicht: man sagt die Funktionen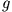 
und 
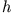vertauschen nicht miteinander.
Wir werden jedoch sehen, dass
die Poissonklammern ein nützliches Instrument sind, um Erhaltungsgrößen eines mechanischen Systems aufzuspüren. Dazu betrachten wir die
totale Zeitableitung von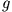
woraus sich mit Hilfe der Hamilton'schen Bewegungsgleichungen
ergibt. Ist 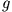nicht explizit zeitabhängig und vertausch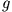t mit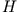 
, so ist 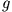offenbar eine Erhaltungsgröße des Systems, das durch die
Hamilton-Funktion beschrieben wird.
Insbesondere ist die Hamilton-Funktion selbst eine Erhaltungsgröße, falls sie nicht explizit zeitabhängig ist, da
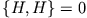. Man kann zeigen, dass alle Symmetrietransformationen des Systems mit 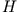vertauschen und erhält so systematisch die
Erhaltungsgrössen des mechanischen Systems. Darüber hinaus gelten die folgenden Aussagen:
- (i)
- Hamiltons Bewegungsgleichungen
- (ii)
- Impulse und Koordinaten
M. Keim, H.J. Lüdde
