Wir definieren die Hamilton-Funktion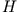 
eines mechanischen Systems (benutze die Definition des generalisierten Impulses
)
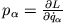und wollen zunächst zeigen, unter welchen Bedingungen sie eine Erhaltungsgröße ist
Mit Hilfe der Lagrange-Gleichung für
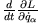und der Kettenregel für
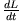findet man
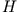ist also eine Erhaltungsgröße, wenn die Lagrange-Funktion nicht explizit von der Zeit abhängt. Die Hamilton-Funktion ist nun
Ausgangspunkt
einer Reformulierung der Bewegungsgleichung der klassischen Mechanik. Dazu betrachten wir die folgenden partiellen Ableitungen von
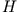
Die resultierenden Bewegungsgleichungen für die generalisierten Koordinaten und Impulse
nennt man die Hamilton'schen Gleichungen oder die kanonischen Bewegungsgleichungen. Sie sind äquivalent zu den Lagrange-Gleichungen und damit
auch zu den Newton'schen Bewegungsgleichungen.
Die Hamilton Funktion eines Systems von Massenpunkten ist identisch mit der totalen mechanischen Energie, wenn die Zwangsbedingungen des
Systems (i) holonom, d.h. unabhängig von der Geschwindigkeit der Massenpunkte, sowie (ii) skleronom, d.h. zeitunabhängig sind.
In diesem Fall
sind die generalisierten Koordinaten nur von den kartesischen Koordinaten der Massenpunkte abhängig, so dass
:
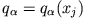Man kann zeigen, dass unter
solchen Zwangsbedinungen die kinetische Energie eine homogene quadratische Funktion der generalisierten Geschwindigkeit ist, d.h.
Somit folgt
und man erhält für (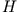
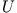ist unabhängig von der generalisierten Geschwindigkeit)
Da 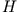eine Erhaltungsgröße ist, ist auch 
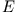eine Erhaltungsgröße, wie wir das von einem konservativen System erwarten.
M. Keim, H.J. Lüdde
