B8.5 Kurbelmechanismus
Der Kurbelmechanismus dient dazu, eine Translations- in eine Rotationsbewegung umzuwandeln. Anwendungen
sind vielfältig, z.B. der Antrieb der Kurbelwelle im Auto durch die Kolbenbewegung im Zylinder.
Abbildung 8.7:
Kurbelmechanismus
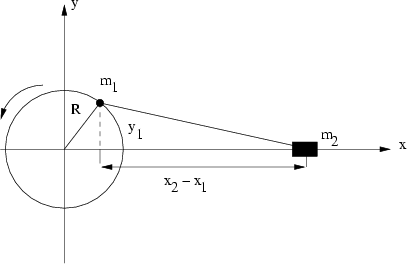 |
Wir wollen die Bewegung der Massen 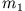 und
und 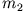 beschreiben. Grundsätzlich haben wir für die
beschreiben. Grundsätzlich haben wir für die 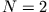 Massenpunkte
Massenpunkte 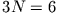 Freiheitsgrade, die durch die folgenden Zwangsbedingungen eingeschränkt werden:
Freiheitsgrade, die durch die folgenden Zwangsbedingungen eingeschränkt werden:
Offenbar legen die 6 Zwangsbedingungen die 6 Freiheitsgrade der Massenpunkte vollständig fest.
Es verbleibt kein Freiheitsgrad, der noch durch die Bewegungsgleichung zu bestimmen wäre. Man
erhält aus (2) und (3) mit der Anfangsbedingung 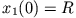 ,
, 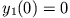 ,
,
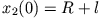
und aus (4) - (6)
Es gibt einen interessanten Sonderfall für 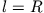 und die Anfangsbedingung
und die Anfangsbedingung 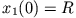 ,
, 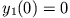 ,
, 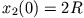 :
:
In diesem Fall schwingt die Kurbel über die Mitte des Kreises hinaus. Mit der Anfangsbedingung
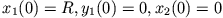 erhält man hingegen
erhält man hingegen 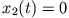 , d.h. die Masse
, d.h. die Masse 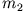 bleibt im Mittelpunkt und
bleibt im Mittelpunkt und 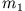 bewegt sich im Abstand
bewegt sich im Abstand
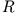 um
um 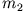 herum.
herum.
B8.6 Bewegung eines Massenpunktes in einem Trichter
Abbildung 8.8:
Bewegung auf der Innenseite eines Kegels
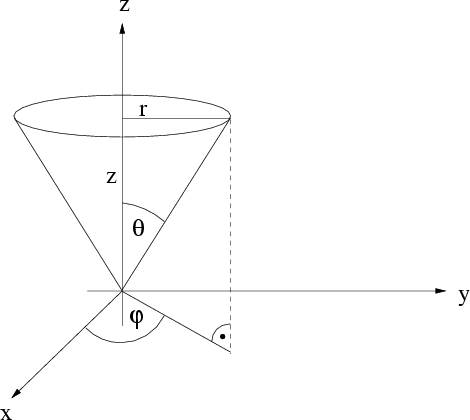 |
Wegen der Zylindersymmetrie des Systems wählen wir Zylinderkoordinaten 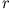 ,
, 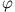 und
und 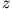 mit
mit
Der Massenpunkt bewegt sich auf der Innenseite eines Kegels
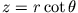 . Somit verbleiben 2 Freiheitsgrade, die wir durch
generalisierte Koordinaten (z.B.
. Somit verbleiben 2 Freiheitsgrade, die wir durch
generalisierte Koordinaten (z.B. 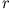 ,
, 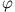 ) beschreiben müssen. Zunächst beginnt man mit der Bestimmung der Lagrange-Funktion:
) beschreiben müssen. Zunächst beginnt man mit der Bestimmung der Lagrange-Funktion:
Unter Brücksichtigung der Kegelfläche findet man
und somit
Wir sehen, die Lagrange-Funktion ist nur noch von den zwei generalisierten Koordinaten 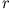 und
und 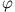 abhängig,
entsprechend der beiden Freiheitsgrade,
die für eine Bewegung auf einer Fläche möglich sind. Wir sehen auch, dass die Bestimmung der generalisierten Koordinaten nicht eindeutig ist:
Wir hätten über die Zwangsbedingung genauso gut
abhängig,
entsprechend der beiden Freiheitsgrade,
die für eine Bewegung auf einer Fläche möglich sind. Wir sehen auch, dass die Bestimmung der generalisierten Koordinaten nicht eindeutig ist:
Wir hätten über die Zwangsbedingung genauso gut 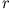 anstatt
anstatt 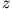 eliminieren können. Ohne weitere Rechnung erkennt man, dass
eliminieren können. Ohne weitere Rechnung erkennt man, dass 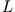 nicht von
nicht von 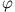 abhängt.
Offenbar ist
abhängt.
Offenbar ist 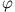 eine zyklische Koordinate mit
eine zyklische Koordinate mit
Die Erhaltungsgröße 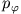 entspricht dem Drehimpuls des Massenpunktes bezüglich der z-Achse.
Somit verbleibt noch die Lagrange-Gleichung für
entspricht dem Drehimpuls des Massenpunktes bezüglich der z-Achse.
Somit verbleibt noch die Lagrange-Gleichung für 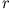
Nach einigen Umformungen ergibt sich
Abbildung 8.9:
Bewegung eines Massenpunktes in einem Trichter bei 'horizontaler' Anfangsgeschwindigkeit.
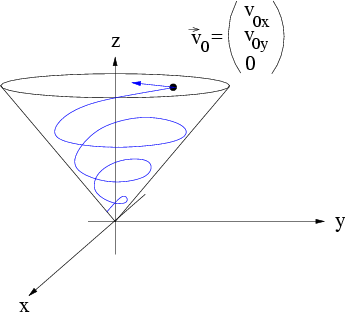 |
M. Keim, H.J. Lüdde

![]() und
und ![]() beschreiben. Grundsätzlich haben wir für die
beschreiben. Grundsätzlich haben wir für die ![]() Massenpunkte
Massenpunkte ![]() Freiheitsgrade, die durch die folgenden Zwangsbedingungen eingeschränkt werden:
Freiheitsgrade, die durch die folgenden Zwangsbedingungen eingeschränkt werden:

![]() ,
, ![]() und
und ![]() mit
mit
