8.2.1 Generalisierte Koordinaten

Betrachten wir ein System aus Massenpunkten, so haben wir gesehen, dass ohne weitere Einschränkungen dieses System Freiheitsgrade besitzt. In der Regel sind jedoch die Massenpunkte einer Reihe von Zwangsbedingungen unterworfen: einige Massenpunkte sind fest miteinander verbunden und formen einen starren Körper, einige Massenpunkte können sich nur auf einer vorgegebenen Fläche oder Raumkurve (Achterbahn!) bewegen. Jede dieser Zwangsbedingungen reduziert die Zahl der Freiheitsgrade, so dass bei Zwangsbedingungen die Massenpunkte nur noch Freiheitsgrade besitzen. Diese reduzierte Zahl von Freiheitsgraden wollen wir auf eine Zahl von verallgemeinerte (generalisierte) Koordinaten abbilden. Der Begriff 'generalisiert' impliziert, dass diese Koordinate nicht mehr ausschließlich die Dimension einer Länge haben müssen: es könnten Winkel, Energie oder dimensionslose Größen als generalisierte Koordinaten geeignet sein, um die Zwangsbedingungen zu berücksichtigen.

Beispiele

B8.1 Das ebene Pendel

Die Pendelmasse eines ebenen Pendels wird zu jeder Zeit durch eine x- und y- Koordinate beschrieben, scheint also 2 Freiheitsgrade zu besitzen. Das ist aber nicht wahr: durch den Pendelfaden der festen Länge kann sich das Pendel nur auf einer Kreisbahn um die Aufhängung bewegen.

Abbildung 8.4: Zwangsbedingung konst. im mathematischen Pendel.

Es gibt also eine Zwangsbedingung

welche die Zahl der Freiheitsgrade auf 1 reduziert. Gesucht ist somit eine generalisierte Koordinate, die diese Zwangsbedingung beinhaltet. Aus Erfahrung wissen wir, dass es sich bei der Zwangsbedingung um eine trigonometrische Relation handelt

Unsere einzige generalisierte Koordinate ist offenbar ein Winkel ( ).

B8.2 Bewegung auf einer Kugel (z.B. Erdoberfläche)

Zur Beschreibung eines Massenpunktes auf der Erdoberfläche sind offenbar 2 generalisierte Koordinaten notwendig, denn die Zahl der Freiheitsgrade (3) wird um eine Zwangsbedingung

reduziert. Wir suchen Koordinaten und , die diese Zwangsbedingung erfüllen und probieren

und sind offenbar wieder Winkel und tatsächlich wissen wir aus Erfahrung, dass jede Position auf der Erde durch die Angabe zweier Winkel (geographische Länge und Breite) vollständig bestimmt ist.

Abbildung 8.5: Schiefe Ebene

B8.3 Bewegung auf einer schiefen Ebene

Die Bewegung auf einer schiefen Ebene wird durch die Zwangsbedingung

beschrieben. D.h. die Koordinaten des Massenpunkts müssen zu jeder Zeit die Zwangsbedingung erfüllen.

B8.4 Bewegung unter zeitabhängigen Zwangsbedingungen

Abbildung 8.6: Bewegung einer Perle entlang eines unendlich langen, starren, rotierenden oder wippenden Drahtes

Beispiele hierfür sind der rotierende Draht

und die Zwangsbedingung, die durch eine Wippe hervorgerufen wird

Man klassifiziert die Zwangsbedingungen nach starren (skleronomen) oder zeitlich veränder-lichen (rheonomen) Zwangsbedingungen. Ist eine Zwangsbedingung stetig bzw. lässt sich die Zwangsbedingung als totales Differential formulieren, so nennt man sie holonom.

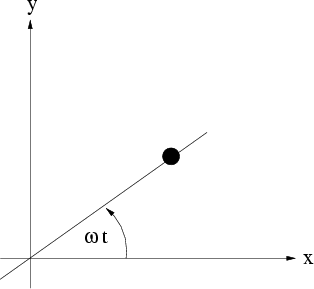Man sieht schon, dass es im allgemeinen nicht einfach sein wird generalisierte Koordinaten zu finden, die alle Zwangsbedingungen enthalten. Wir wollen jedoch annehmen, dass wir generalisierte Koordinaten ( ) für ein System von Massenpunkten mit Zwangsbedingungen kennen. Diesen generalisierten Koordinaten lassen sich generalisierte Geschwindigkeiten ( ) zuordnen. Ferner kennen wir den Zusammenhang zwischen den und den kartesischen Koordinaten , so dass sich mit

die Lagrange-Funktion, die wir zunächst in kartesischen Koordinaten berechnet haben, bezüglich der generalisierten Koordinaten und Geschwindigkeiten ausdrücken lässt

Damit erhält man mit den selben Argumenten wie in Abschnitt 8.1.2 die Lagrange-Gleichungen in den generalisierten Koordinaten

Der Vorteil gegenüber den Newton'schen Bewegungsgleichungen ist, dass die Lagrange-Gleichungen immer die selbe Form haben, unabhängig von der speziellen Wahl der Koordinaten. Ebenfalls analog zu 8.1.2 definiert man die generalisierten Impulse

Auch jetzt gilt: ist aus Symmetriegründen nicht von abhängig, so ist eine (eventuell abstrakte) Erhaltungsgröße. heißt in diesem Fall 'zyklische' Koordinate und enthält eine (eventuell abstrakte) Symmetrie.