Wir sind jetzt in der Lage das Prinzip der minimalen Wirkung auszuwerten. Mit 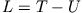 ist die Lagrangefunktion also abhängig von Ort und
Geschwindigkeit aller Teilchen eines Systems von
ist die Lagrangefunktion also abhängig von Ort und
Geschwindigkeit aller Teilchen eines Systems von 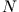 Massenpunkten
Massenpunkten
Das Extremalprinzip
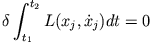 |
(8.2) |
erfordert somit eine Lösung (
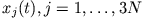 ), für die gilt
), für die gilt
Dies sind die Langrange'sche Bewegungsgleichung der Mechanik und wir wollen jetzt zeigen, dass sie äquivalent zu den Newton'schen
Bewegungsgleichungen sind. Dazu müssen wir berücksichtigen, dass die Lagrange-Funktion nur für konservative Kräfte formuliert werden kann.
Nur wenn
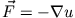 (also
(also 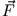 konservativ ist), lässt sich das Bewegungsproblem durch ein Potential
konservativ ist), lässt sich das Bewegungsproblem durch ein Potential 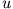 charakterisieren. Das Potential ist aber nur eine
Funktion des Ortes. Für einen einzelnen Massenpunkt gilt dann ohne Beschränkung der Allgemeinheit
charakterisieren. Das Potential ist aber nur eine
Funktion des Ortes. Für einen einzelnen Massenpunkt gilt dann ohne Beschränkung der Allgemeinheit
Aus den Lagrange-Gleichungen folgt somit
unmittelbar die Newton'sche Bewegungsgleichung.
Wir können aber noch eine weitere interessante Eigenschaft aus den Langrange-Gleichungen ablesen. Dazu betrachten wir
d. h. wir können die Langrange Gleichung in der Form schreiben
Ist die Lagrange-Funktion von einer der kartesischen Komponente unabhängig,
so folgt daraus sofort, dass der Impuls dieser Komponente
eine Erhaltungsgröße ist
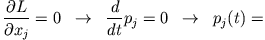 konst. konst. |
|
Man bezeichnet die Koordinate 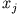 , für die
, für die
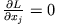 ist als 'zyklische Koordinate'.
Sie enthält offenbar eine Symmetrie des Potentials: man nennt das
System translationsinvariant in der zyklischen Koordinate. Diese Translantionsinvarianz ist wiederum äquivalent zur Erhaltung des Impulses,
welcher der zyklischen Koordinate zugeordnet ist. Diese Äquivalenz zwischen Symmetrien und Erhaltungsgrößen ist ein wesentliches Element der
analytischen Mechanik. In seiner verallgemeinerten Form wurde von Emily Noether (1882-1935) bewiesen, dass die Invarianz der Lagrange-Funktion
gegenüber Symmetrietransformationen immer die Existenz einer Erhaltungsgröße zur Folge hat. Nun wird man mit Recht behaupten, dass sich der
Aufwand zur Ableitung der Lagrange-Gleichung bisher kaum gelohnt habe: solange man sich auf kartesiche Koordinaten beschränkt, hätte man
schließlich auch die Newton'sche Bewegungsgleichung diskutieren können. Es ist also an der Zeit, dass wir das Konzept, das hinter dem
Hamilton-Prinzip steckt, auf einer verallgemeinerten Basis erweitern.
ist als 'zyklische Koordinate'.
Sie enthält offenbar eine Symmetrie des Potentials: man nennt das
System translationsinvariant in der zyklischen Koordinate. Diese Translantionsinvarianz ist wiederum äquivalent zur Erhaltung des Impulses,
welcher der zyklischen Koordinate zugeordnet ist. Diese Äquivalenz zwischen Symmetrien und Erhaltungsgrößen ist ein wesentliches Element der
analytischen Mechanik. In seiner verallgemeinerten Form wurde von Emily Noether (1882-1935) bewiesen, dass die Invarianz der Lagrange-Funktion
gegenüber Symmetrietransformationen immer die Existenz einer Erhaltungsgröße zur Folge hat. Nun wird man mit Recht behaupten, dass sich der
Aufwand zur Ableitung der Lagrange-Gleichung bisher kaum gelohnt habe: solange man sich auf kartesiche Koordinaten beschränkt, hätte man
schließlich auch die Newton'sche Bewegungsgleichung diskutieren können. Es ist also an der Zeit, dass wir das Konzept, das hinter dem
Hamilton-Prinzip steckt, auf einer verallgemeinerten Basis erweitern.
M. Keim, H.J. Lüdde
![]() ist die Lagrangefunktion also abhängig von Ort und
Geschwindigkeit aller Teilchen eines Systems von
ist die Lagrangefunktion also abhängig von Ort und
Geschwindigkeit aller Teilchen eines Systems von ![]() Massenpunkten
Massenpunkten