Die entscheidende Frage ist, wie bestimmen wir eine Funktion y(x) so, dass das Integral
extremal wird?
Abbildung 8.3:
Zwei Wege mit
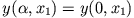und
.
 |
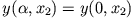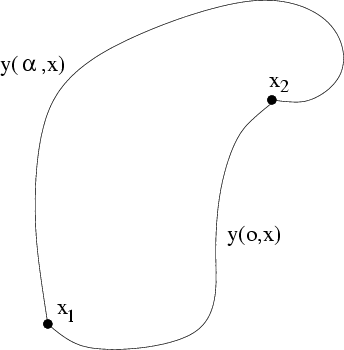Dabei sind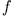 
und die Grenzen 
, 
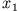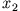vorgegeben. Die Funktion 
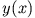muss jetzt so variiert werden, dass 
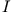extremal
wird. Nehmen
wir an, die Schar möglicher Lösungen
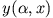lässt sich durch einen zusätzlichen Parameter 
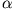charakterisieren, so dass
mit der Bedingung, dass
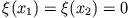. (Alle Lösungen der Schar sollen in 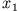und 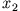übereinstimmen).
Dann ist für eine beliebige Funktion aus dieser Schar
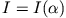mit
und die Frage nach dem Extremum lautet
Daraus ergibt sich (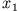 und 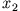sind Konstanten) mit Hilfe der Kettenregel
Integriert man den 2. Term partiell, so erhält man
mit dem gewählten Ansatz für
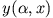gilt
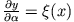, so dass die Variation an den
Randpunkten verschwindet
Somit erhalten wir
Damit
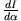für beliebige Funktionen 
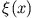verschwindet, muss gelten
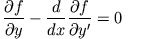 Euler-Gleichung (1744) |
|
Da 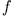vorgegebenen ist, bildet die Euler-Gleichung eine Differentialgleichung für .
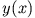M. Keim, H.J. Lüdde
