Wir werden sehen, dass sich die Newton'sche Bewegungsgleichung aus einem Extremalprinzip ableiten lässt:
dem Hamilton'schen Prinzip der minimalen Wirkung. Es besagt, dass
- von allen möglichen Pfaden zwischen zwei Punkten innerhalb eines vorgegebenen Zeitintervalls die Dynamik eines Systems durch denjenigen Pfad
beschrieben wird, für den das Zeitintegral über die Differenz aus kinetischer und potentieller Energie minimal ist.
Mathematisch bedeutet dies, dass
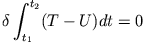 |
(8.1) |
Der Integrand 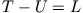 heißt Langrangefunktion - besitzt die Dimension einer Energie, das Integral somit Energie*Zeit=Wirkung. Die Minimierung
bedeutet, dass ein Massenpunkt in gegebener Zeit möglichst wenig Energie aufwenden möchte, um von einem Anfangsort zu einem Endpunkt zu
heißt Langrangefunktion - besitzt die Dimension einer Energie, das Integral somit Energie*Zeit=Wirkung. Die Minimierung
bedeutet, dass ein Massenpunkt in gegebener Zeit möglichst wenig Energie aufwenden möchte, um von einem Anfangsort zu einem Endpunkt zu
Abbildung 8.1:
Suche nach dem ökonomischsten Weg zwischen
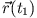 und
und
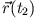 .
.
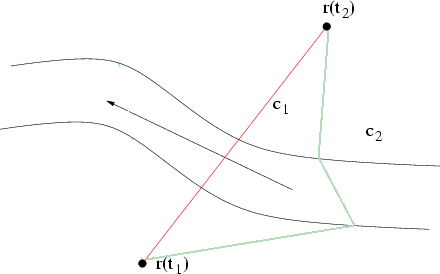 |
kommen. Stellen Sie sich vor, Sie müssten einen Fluss schwimmend überqueren, um von Ort
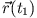 nach
nach
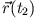 zu kommen. Der
kürzeste Weg
entspricht dem Pfad
zu kommen. Der
kürzeste Weg
entspricht dem Pfad 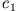 .
Aber ist dies auch der ökonomischste? Um den Fluss auf
.
Aber ist dies auch der ökonomischste? Um den Fluss auf 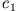 zu überqueren, müssen Sie viel Energie aufwenden, um gegen
die Strömung anzukämpfen. Vernünftiger wäre es, sich entlang des Pfades
zu überqueren, müssen Sie viel Energie aufwenden, um gegen
die Strömung anzukämpfen. Vernünftiger wäre es, sich entlang des Pfades 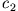 abtreiben zu lassen, um dann auf dem
bequemeren Landweg etwas schneller
zu laufen, damit Sie in der gleichen Zeit
abtreiben zu lassen, um dann auf dem
bequemeren Landweg etwas schneller
zu laufen, damit Sie in der gleichen Zeit 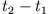 Ihr Ziel erreichen.
Ihr Ziel erreichen.
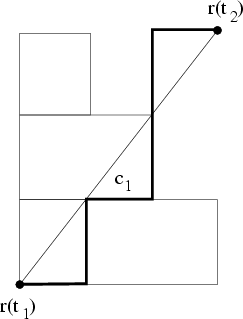
Abbildung 8.2:
Suche nach dem kürzesten Weg bei gegebener Zwangsbedingung
 |
Eine andere Aufgabe wäre in vorgegebener Zeit
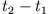 von
von
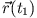 nach
nach
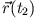 zu laufen, aber unter der Zwangsbedingung, dass Sie nur auf vorgegebenen Fußwegen Ihr Ziel erreichen dürfen.
Der direkte Weg
zu laufen, aber unter der Zwangsbedingung, dass Sie nur auf vorgegebenen Fußwegen Ihr Ziel erreichen dürfen.
Der direkte Weg 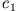 wäre
versperrt und
wäre
versperrt und 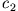 wäre der ökonomischste Weg unter den 'Fußweg-alternativen'.
Warum die Lagrangefunktion
wäre der ökonomischste Weg unter den 'Fußweg-alternativen'.
Warum die Lagrangefunktion 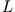 und nicht die Gesamtenergie
und nicht die Gesamtenergie 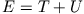 das Wirkungsprinzip bestimmt, liegt daran, dass sich nur aus (8.1) die
Newton'sche Bewegungsgleichung ableiten lässt. (In verallgemeinerter Form lässt sich die Diskussion auch auf dissipative bzw. explizit
zeitabhängige Systeme erweitern.)
das Wirkungsprinzip bestimmt, liegt daran, dass sich nur aus (8.1) die
Newton'sche Bewegungsgleichung ableiten lässt. (In verallgemeinerter Form lässt sich die Diskussion auch auf dissipative bzw. explizit
zeitabhängige Systeme erweitern.)
M. Keim, H.J. Lüdde