7.5 Beispiele

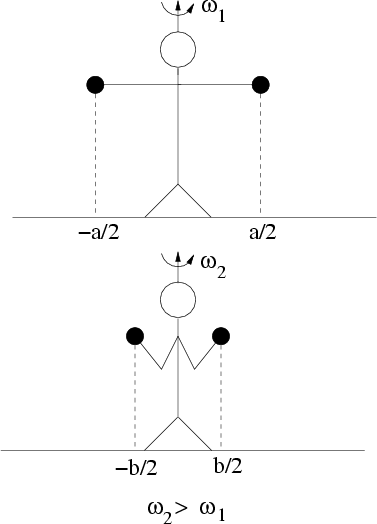
B7.2 Pirouetteneffekt

Abbildung 7.9: Pirouetteneffekt

Ein Beispiel für die Erhaltung des Drehimpulses ist der Pirouetteneffekt. Durch die zeitliche Änderung des Trägheitsmomentes bezogen auf die Drehachse ändert sich bei konstantem Drehimpuls die Winkelgeschwindigkeit

Betrachtet man die Arme der Figur idealisiert als dünnen Stab, so ergibt sich mit

wobei die Armlänge bei ausgestrecktem Arm und der Körperradius bezogen auf die Längsachse bedeuten.

B7.3 Torsionspendel

Abbildung 7.10: Torsionspendel

Ein Torsionspendel besteht aus einer kreisförmigen Scheibe, die mittig senkrecht zur Scheibenfläche an einem Stahlseil aufgehängt ist. Für kleine Drehwinkel stellt sich eine harmonische Torsionsschwingung um die Ruhelage ein. Das resultierende Drehmoment ist proportional zum Auslenkwinkel , wobei eine Materialkonstante (die Torsionskonstante) bedeutet. Die Änderung des Drehimpulses ist gleich dem Drehmoment

Aus dieser Gleichung für den harmonischen Oszillator folgt sofort die Oszillatorfrequenz und die Periode

B7.4 Physikalisches Pendel

Abbildung 7.11: Physikalisches Pendel

Im Gegensatz zum mathematischen Pendel, das Pendelfaden und Masse idealisiert, besteht das physikalische Pendel aus einem realistischen starren Körper, der um einen Aufhänge-punkt schwingt. Es folgt wieder aus dem Drehimpulssatz

mit der Frequenz und Periode

Interessant ist der Grenzfall , d.h. das Pendel wird im Schwerpunkt (SP) aufgehängt: in diesem Fall ist , d.h. das Pendel befindet sich für jede Auslenkung in Ruhe, es dauert also unendlich lange, bis die Anfangsauslenkung wieder erreicht wird.

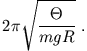B7.5 Rollender Zylinder auf schiefer Ebene

Abbildung 7.12: Rollende Zylinder

Zwei äußerlich identische Zylinder mit Radius und der selben Masse rollen die selbe schiefe Ebene unter identischer Anfangsbedingung hinunter. Zylinder (2) erreicht das Ende der schiefen Ebene nach kürzerer Zeit als Zylinder (1). Warum? Zylinder (1) ist innen hohl, die Masse im Zylindermantel konzentriert, während Zylinder (2) eine homogene Massenverteilung besitzt. Die kinetische Rotationsenergie lautet

Sie ist in beiden Fällen gleich, da die Zylinder aus der gleichen Höhe starten. Da aber die Trägheitsmomente verschieden sind

und somit ist, folgt daraus , weil

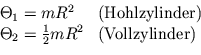B7.6 Atwood Maschine

Abbildung 7.13: Atwood Maschine

Zwei Lasten und sind durch ein Seil über eine feste Rolle mit Trägheitsmoment verbunden. Stelle die Bewegungsgleichung für diese Atwood'sche Fallmaschine auf. Es gibt zunächst eine Bewegungsgleichung für jeden der 3 Körper ( und entsprechen den jeweiligen Seilspannungen, die als Drehmomente an der festen Rolle angreifen):

Da das Seil beide Massen schlupffrei verbindet, gibt es die einschränkende Bedingung

Somit erhalten wir 3 Gleichungen für , und mit der Auflösung

B7.7 Kräftefreier Kreisel - Nutation

Abbildung 7.14: Kräftefreier Kreisel (Nutation der Figurenachse)

Ein kräftefreier Kreisel ist ein Körper, der bezüglich einer ausgezeichenten Achse (Figurenachse), die durch den Schwerpunkt verläuft rotationssymmetrisch ist, und der im Schwerpunkt gelagert ist. Wird der Kreisel so gedreht, dass Figurenachse und momentante Drehachse zusammenfallen, so sind Drehachse, Figurenachse und Richtung des Drehimpulses gleichgerichtet. Wird durch das Anfangsdrehmoment, mit dem man den Kreisel in Bewegung versetzt, die Drehachse gegenüber der Figurenachse geneigt (z.B. durch einen leichten Schlag gegen die Figurenachse des sich bereits drehenden Kreisels), so sind und nicht mehr gleichgerichtet: in diesem Fall dreht sich die Figurenachse auf einem Nutationskegel. und sind wegen immer dann nicht gleichgerichtet, wenn der Trägheitstensor zwar diagonal ist, die Drehachse aber nicht mit einer Hauptachse zusammenfällt. Man beachte: Auch wenn diagonal ist, sind und im allgemeinen nicht gleich gerichtet. Beispiel:

und sind gleich gerichtet, wenn mit einer Hauptachse zusammenfällt oder . (Bei symmetrischen Körpern ist die Figurenachse immer auch eine Hauptachse des Körpers.)

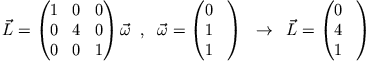B7.8 Schwerer Kreisel (Gyroskop) - Präzession

Abbildung 7.15: Schwerer Kreisel (Präzession der Figurenachse)

Betrachte die Rotation einer Kreisscheibe ( ) um eine Hauptachse senkrecht zur Scheibe durch ihren Schwerpunkt. Für diesen Fall ist diagonal

und man findet wegen

und

schließlich

Da die Scheibe nicht im Schwerpunkt sondern am Ende einer Achse der Länge gelagert ist, wirkt die Gravitation auf die Scheibe ( ) und erzeugt das Drehmoment bezüglich des Auflagepunktes.

Abbildung 7.16: Zur Drehung der Figurenachse im schweren Kreisel.

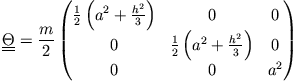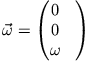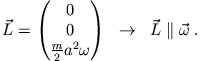Der Kreisel reagiert auf das Drehmoment mit einer Drehimpulsänderung , die sich zum Drehimpuls das Kreisels addiert und die Figurenachse um den Winkel dreht

Die Ausweichbewegung des Kreisels aufgrund einer äußeren Kraft nennt man Präzession. Die Winkelgeschwindigkeit der Präzession ist