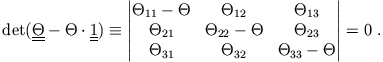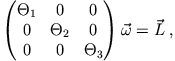Wir haben gesehen, dass im allgemeinen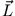 
und
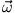nicht gleich gerichtet sind. Wir können aber immer ein körperfestes
Achsensystem finden, in dem der Trägheitstensor diagonal wird und somit 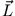und
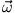gleichgerichtet sein können. Dieses
ausgezeichnete System nennt man Hauptachsensystem, die zugehörigen Diagonalelemente des transformierten Trägheitstensors
nennt man Hauptträgheitsmomente. Mathematisch erhält man das Hauptachsensystem aus dem Ansatz
Man nennt diese Gleichung eine Eigenwertgleichung: Gesucht sind diejenigen Vektoren
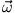, die der Trägheitstensor
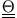in sich selbst abbildet (gestreckt oder gestaucht).
Die 3 Hauptachsenmomente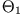 
, 
, 
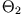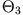erhält man aus der Bedingungsgleichung für die Existenz
einer nichttrivialen Lösung des homogenen Gleichungssystems (Säkulargleichung oder charakteristisches Polynom)
Diese kubische Gleichung besitzt nur reelle Lösungen, da
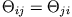. Haben wir das Hauptachsensystem gefunden,
so gilt, falls
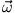entlang einer Hauptachse gerichtet ist
dass
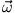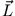und gleichgerichtet sind. Ist
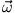konstant, so folgt unmittelbar, dass auch
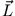für diesen Fall konstant ist. Für ein beliebiges körperfestes System ist das nicht der Fall (siehe Hantel:
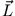ist zeitabhängig, obwohl
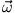konstant ist).
Daraus lässt sich folgende Interpretation ableiten:
- (i)
- Ist
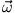konstant, so ist 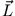konstant, falls wir ein Hauptachsensystem gefunden haben (
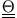ist diagonal) und die Drehachse einer Hauptachse entspricht.
- (ii)
- Ist 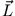konstant, wirken keine Drehmomente.
Die Außerdiagonalelemente des Trägheitstensors sind also ein Maß für Drehmomente, die an den Lagern
der Drehachse angreifen. Diese Lagermomente verschwinden, wenn wir den starren Körper um eine seiner Symmetrieachsen (allgemeiner
Hauptachsen) rotieren lassen.
M. Keim, H.J. Lüdde
