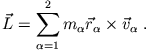Bezogen auf ein körperfestes Schwerpunktsystem ist der Drehimpuls eines diskreten starren Körpers
Da Allgemein
gilt, folgt unmittelbar
Schreibt man diesen Ausdruck für eine beliebige Komponente (z.B. 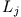 ) aus, so erhält man
) aus, so erhält man
bzw. in Vektorschreibweise
Aus der linearen Algebra wissen wir, dass die Vektoren 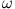 und
und 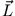 im allgemeinen nicht gleichgerichtet sind, wenn die Matrix
im allgemeinen nicht gleichgerichtet sind, wenn die Matrix
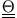 nicht diagonal ist (dass
nicht diagonal ist (dass
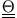 diagonal ist, ist nicht hinreichend, damit
diagonal ist, ist nicht hinreichend, damit
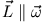 . Es muss zusätzlich
. Es muss zusätzlich
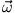 parallel zu einer der Hauptachsen (siehe 7.4) gerichtet sein (siehe auch
Beispiel B7.7). D.h. der Drehimpuls eines rotierenden Körpers wird im allgemeinen in eine andere Richtung zeigen als die Drehachse!
parallel zu einer der Hauptachsen (siehe 7.4) gerichtet sein (siehe auch
Beispiel B7.7). D.h. der Drehimpuls eines rotierenden Körpers wird im allgemeinen in eine andere Richtung zeigen als die Drehachse!
B7.1 Rotierende Hantel
Abbildung 7.8:
Rotierende Hantel
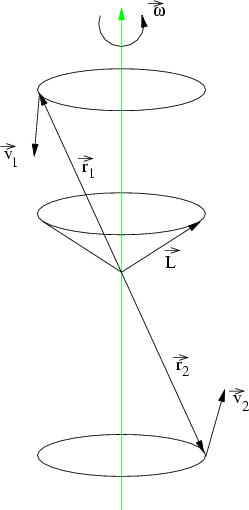 |
Für die Geschwindigkeiten der beiden Massen 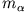 gilt
gilt
und für den Drehimpuls
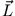 steht senkrecht auf
steht senkrecht auf 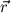 und
und 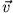 . Da aber
. Da aber
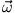 nicht senkrecht auf
nicht senkrecht auf 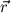 steht, müssen
steht, müssen
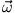 und
und 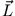 einen Winkel zueinander besitzen.
Hinzu kommt, dass
einen Winkel zueinander besitzen.
Hinzu kommt, dass 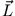 zeitlich nicht konstant ist, sondern sich auf einem Kegel um die Drehachse mit der Winkelgeschwindigkeit
zeitlich nicht konstant ist, sondern sich auf einem Kegel um die Drehachse mit der Winkelgeschwindigkeit
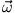 bewegt. Da aber
bewegt. Da aber 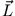 von der Zeit abhängt, ist
von der Zeit abhängt, ist
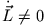 . Wir wissen aus dem Drehimpulssatz,
dass eine zeitliche Änderung des Drehimpulses nur durch ein Drehmoment hervorgerufen werden kann, also
. Wir wissen aus dem Drehimpulssatz,
dass eine zeitliche Änderung des Drehimpulses nur durch ein Drehmoment hervorgerufen werden kann, also
Andererseits gilt für einen zeitlich konstanten Trägheitstensor
so dass wir eine Bewegungsgleichung für den rotierenden Körper erhalten (bezogen auf ein körperfestes Schwerpunktsystem)
(Beachte die Analogie zur Newton'schen Bewegungsgleichung
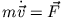 .)
Wirken keine äußeren Drehmomente sind
.)
Wirken keine äußeren Drehmomente sind 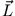 und somit
und somit
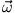 konstant (unter der Voraussetzung, dass
konstant (unter der Voraussetzung, dass
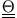 zeitlich konstant ist).
zeitlich konstant ist).
M. Keim, H.J. Lüdde
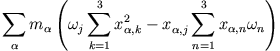
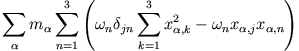
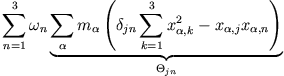
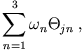
![]() gilt
gilt