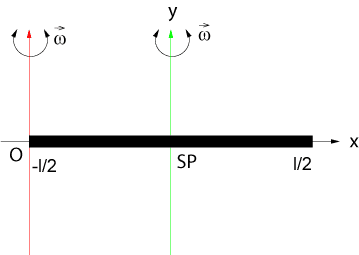
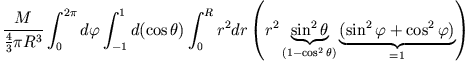(i) Trägheitsmoment eines dünnen Stabes
Ein sehr dünner Stab der Länge 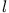 habe die Masse
habe die Masse 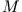 , die homogen über den Stab verteilt sei. Folglich liegt der Schwerpunkt in der Mitte des
Stabes und die Massendichte
, die homogen über den Stab verteilt sei. Folglich liegt der Schwerpunkt in der Mitte des
Stabes und die Massendichte
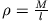 ist konstant. Die Drehache ist senkrecht zum Stab gewählt.
ist konstant. Die Drehache ist senkrecht zum Stab gewählt.
Abbildung 7.3:
Dünner Stab
 |
Das entsprechende Trägheitsmoment
ist dann
Nach dem Steiner'schen Satz ergibt sich das Trägheitsmoment bezogen auf eine parallele Achse durch den Endpunkt des Stabes zu
(ii) Trägheitsmoment einer kreisförmigen Scheibe
Eine dünne, kreisförmige Scheibe mit Radius 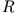 und homogener Masse
und homogener Masse  drehe sich um eine Achse durch den Schwerpunkt senkrecht zur
Scheibenfläche.
drehe sich um eine Achse durch den Schwerpunkt senkrecht zur
Scheibenfläche.
Abbildung 7.4:
Kreisscheibe
 |
Mit
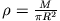 ist
ist
wobei das Volumen der Kreisfläche
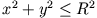 entspricht.
Bei der Transformation von kartesischen Koordinaten in ebene Polarkoordinaten
entspricht.
Bei der Transformation von kartesischen Koordinaten in ebene Polarkoordinaten
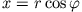 ,
,
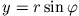 gilt für das
Volumenelement
gilt für das
Volumenelement
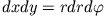 (siehe 'Funktionaldeterminante' im Skript zur Differential- und Integralrechnung) und somit
(siehe 'Funktionaldeterminante' im Skript zur Differential- und Integralrechnung) und somit
bzw.
(iii) Trägheitsmoment eines Zylinders
Abbildung 7.5:
Zylinder
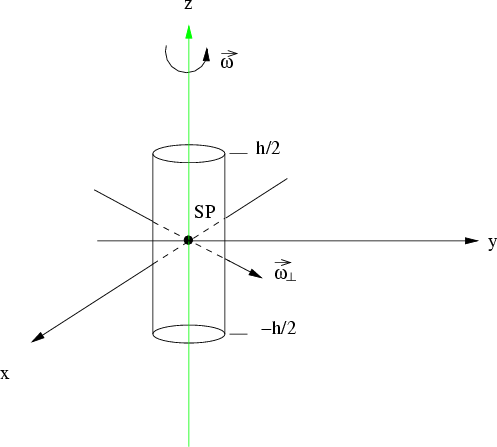 |
Für einen Zylinder der Höhe 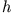 und der Masse
und der Masse 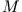 erhält man (
erhält man (
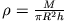 )
)
Die Integration kann leicht in Zylinderkoordinaten ausgeführt werden
Das Trägheitsmoment
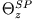 eines Zylinders lässt sich also mit einem Stapel von kreisförmig-en Scheiben der Dicke
eines Zylinders lässt sich also mit einem Stapel von kreisförmig-en Scheiben der Dicke 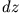 vergleichen.
Für das Trägheitsmoment bezogen auf eine Drehachse senkrecht zur z-Achse erhält man
vergleichen.
Für das Trägheitsmoment bezogen auf eine Drehachse senkrecht zur z-Achse erhält man
und mit
dann
Offenbar zeichnen sich die gewählten Achsen als Symmetrieachsen des Zylinders aus. In diesem Fall gilt für ein beliebiges
Deviationsmoment
(z.B.
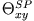 )
)
und mit
schließlich
Wir werden sehen, dass die Deviationsmomente für eine Drehachse, die gleichzeitig eine Symmetrieachse des Körpers ist, immer verschwinden. In
diesem Fall ist der Trägheitstensor diagonal
(Bezüglich der Symmetrieachse des Zylinders).
(iv) Homogene Kugel
Abbildung 7.6:
Kugel
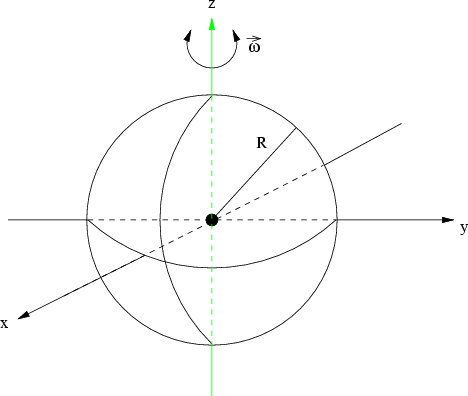 |
Zur Berechnung des Trägheitsmoments einer Kugel mit Radius 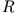 und Masse
und Masse 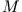 wählt man Kugelkoordinaten mit
wählt man Kugelkoordinaten mit
Aus Symmetriegründen sind die Trägheitsmomente alle gleich, d.h. es gilt exemplarisch
(v) Homogener Quader
Abbildung 7.7:
Quader
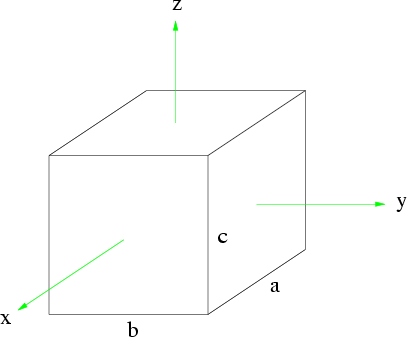 |
Analog gilt
und
Für einen Würfel (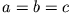 ) findet man
) findet man
M. Keim, H.J. Lüdde
![]() habe die Masse
habe die Masse ![]() , die homogen über den Stab verteilt sei. Folglich liegt der Schwerpunkt in der Mitte des
Stabes und die Massendichte
, die homogen über den Stab verteilt sei. Folglich liegt der Schwerpunkt in der Mitte des
Stabes und die Massendichte
![]() ist konstant. Die Drehache ist senkrecht zum Stab gewählt.
ist konstant. Die Drehache ist senkrecht zum Stab gewählt.
![]() und homogener Masse
und homogener Masse ![]() drehe sich um eine Achse durch den Schwerpunkt senkrecht zur
Scheibenfläche.
drehe sich um eine Achse durch den Schwerpunkt senkrecht zur
Scheibenfläche.
![]() ist
ist
![]() und der Masse
und der Masse ![]() erhält man (
erhält man (
![]() )
)
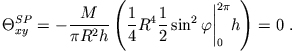
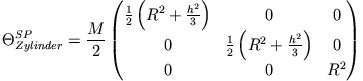
![]() und Masse
und Masse ![]() wählt man Kugelkoordinaten mit
wählt man Kugelkoordinaten mit