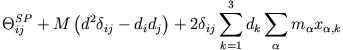Abbildung 7.2:
Zur Geometrie des Parallelachsen-Theorems
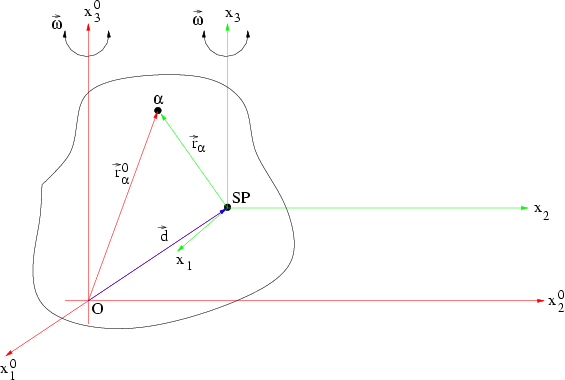 |
Angenommen wir kennen den Trägheitstensor
 für einen Körper bezogen auf eine Drehachse durch den
Schwerpunkt des Körpers, wollen aber den Körper um eine parallele Achse durch einen Punkt
für einen Körper bezogen auf eine Drehachse durch den
Schwerpunkt des Körpers, wollen aber den Körper um eine parallele Achse durch einen Punkt  des starren Körpers drehen. Kann man den
Trägheitstensor
des starren Körpers drehen. Kann man den
Trägheitstensor
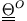 bezogen auf die neue Drehachse durch
bezogen auf die neue Drehachse durch
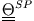 ausdrücken?
Bezeichnet man die Position eines beliebigen Punktes
ausdrücken?
Bezeichnet man die Position eines beliebigen Punktes 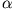 im starren Körper durch
im starren Körper durch
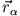 (bezogen auf das Schwerpunktsystem)
bzw.
(bezogen auf das Schwerpunktsystem)
bzw.
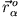 (bezogen auf das
(bezogen auf das 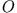 -System), so gilt wegen
-System), so gilt wegen
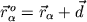 für die Elemente der
Trägheitsmatrix bezogen auf die Drehachse
für die Elemente der
Trägheitsmatrix bezogen auf die Drehachse 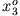
mit
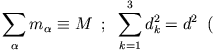 Länge von Länge von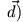 |
|
folgt
Im Schwerpunktsystem gilt: jede Komponente der Schwerpunktkoordinate (hier die k. Komponente) verschwindet im Schwerpunktsystem, also
Man erhält schließlich
Somit können wir den Trägheitstensor bezogen auf eine beliebig verschobene Drehachse berechnen. Für das Trägheitsmoment
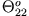 bezogen auf die
bezogen auf die 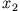 Achse als Drehachse gilt dann z.B.
Achse als Drehachse gilt dann z.B.
Die Differenz der Trägheitsmomente bezogen auf den Schwerpunkt und 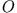 ist gleich der Gesamtmasse des Körpers
ist gleich der Gesamtmasse des Körpers 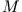 multipliziert mit dem
Abstand zwischen den parallelen Drehachsen.
multipliziert mit dem
Abstand zwischen den parallelen Drehachsen.
M. Keim, H.J. Lüdde

![]() für einen Körper bezogen auf eine Drehachse durch den
Schwerpunkt des Körpers, wollen aber den Körper um eine parallele Achse durch einen Punkt
für einen Körper bezogen auf eine Drehachse durch den
Schwerpunkt des Körpers, wollen aber den Körper um eine parallele Achse durch einen Punkt ![]() des starren Körpers drehen. Kann man den
Trägheitstensor
des starren Körpers drehen. Kann man den
Trägheitstensor
![]() bezogen auf die neue Drehachse durch
bezogen auf die neue Drehachse durch
![]() ausdrücken?
Bezeichnet man die Position eines beliebigen Punktes
ausdrücken?
Bezeichnet man die Position eines beliebigen Punktes ![]() im starren Körper durch
im starren Körper durch
![]() (bezogen auf das Schwerpunktsystem)
bzw.
(bezogen auf das Schwerpunktsystem)
bzw.
![]() (bezogen auf das
(bezogen auf das ![]() -System), so gilt wegen
-System), so gilt wegen
![]() für die Elemente der
Trägheitsmatrix bezogen auf die Drehachse
für die Elemente der
Trägheitsmatrix bezogen auf die Drehachse ![]()

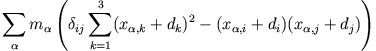
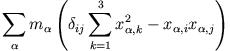
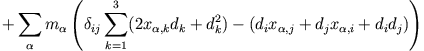
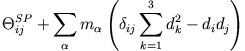
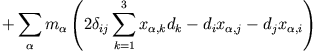
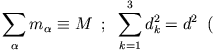 Länge von
Länge von