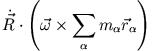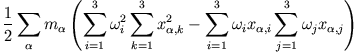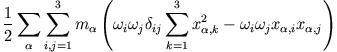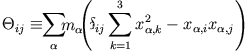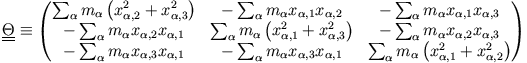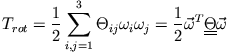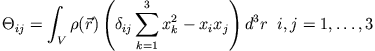Ein starrer Körper ist dadurch definiert, dass die Relativgeschwindigkeit aller Massenpunkte bezogen auf das köperfeste System verschwindet
(
). Somit gilt mit den Ergebnissen aus Kapitel 6.1 für einen beliebigen Massenpunkt 
(
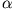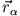Relativkoordinate)
Die kinetische Energie des starren Körpers ist dann
Für den Mischterm gilt (beachte die Definition der Schwerpunktkoordinate)
Da
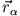die Relativkoordinate bezogen auf den Schwerpunkt ist, ist 
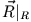die Schwerpunktkoordinate bezogen auf
das Schwerpunktsystem, also
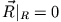. Somit verschwindet der Mischterm und man erhält
Wie bereits intuitiv erwartet, erfolgt die Zerlegung der Bewegung in eine Translation des Schwerpunktes und eine Rotation um eine beliebige
Achse durch den Schwerpunkt. Für das Quadrat des Kreuzprodukts erhält man aus allgemeinen Überlegungen
und somit für die kinetische Rotationsenergie
Auswertung der Skalarprodukte in einem kartesischen Koordinatensystem, d.h. mit
und
ergibt
Definiert man mit
die Matrixelemente des symmetrischen Trägheitstensors
so erhält man für die kinetische Rotationsenergie
(Mathematisch ist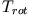 
eine symmetrische Bilinearform).
Die Diagonalelemente der Trägheitsmatrix
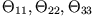nennt man Trägheitsmomente, die außerdiagonalen Elemente
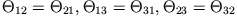Deviations- (oder Lager-) momente. Wir werden später sehen, dass
sie ein Maß für die auf die Drehache wirkenden Drehmomente sind. Haben wir es mit einer kontinuierlichen Massenverteilung der Dichte
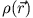zu tun - anstatt mit einem Drahtgittermodell diskreter starr verbundener Massenpunkte 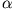- so gilt für die Elemente der
Trägheitsmatrix
wobei die Integration über die kartesischen Komponenten (
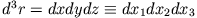) des Volumens 
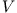des starren Körpers auszuführen
ist.
M. Keim, H.J. Lüdde
