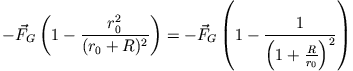Wirkt ein inhomogenes Gravitationsfeld auf einen ausgedehnten Körper, so können die Differenzkräfte innerhalb des Körpers so stark werden,
dass er sich verformt. (bzw. in Bruchstücke zerfällt). Diese Differenzkraft nennt man Gezeitenkraft. Das Phänomen der Verformung in einem
inhomogenen Kraftfeld werden wir in der Elektrostatik und in der Atomphysik unter dem Begriff Polarisation wiederfinden.
Um die Gezeitenkraft, welche die Sonne auf die Erde ausübt, abzuschätzen, wollen wir annehmen, dass sich die Erde auf einer Kreisbahn um die
Sonne bewegt.
Abbildung 6.11:
Rotierendes Schwerpunktsystem von Erde und Sonne.
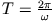ist die Umlaufzeit der Erde.
 |
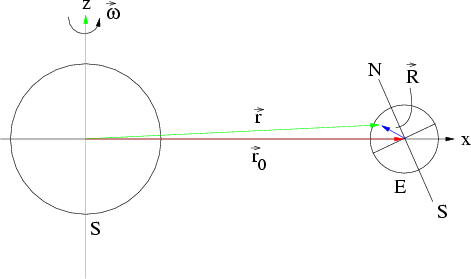Die Keplerbahn ist dann stabil, wenn der Mittelpunkt der Erde im geozentrischen System kräftefrei ist, d.h. im Mittelpunkt der
Erde kompensieren sich Gravitation und Zentrifugalkraft. Für ein beliebiges Massenelement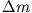 
im Zentrum der Erde gilt dann
im rotierenden
System Erde-Sonne
Ein Massenelement an einem beliebigen anderen Punkt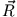 
der Erde ist dagegen nicht kräftefrei. Da er sich mit der gleichen Geschwindigkeit
bewegt wie der Mittelpunkt, ist die Zentrifugalkraft, in diesem Punkt genauso groß. Dagegen ist die Gravitationskraft der Sonne größer oder
Abbildung 6.12:
Zur Gezeitenkraft.
 |
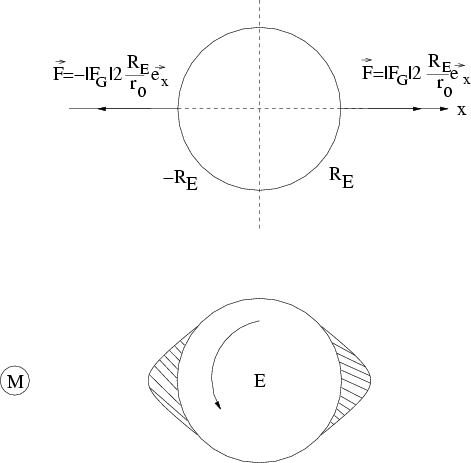kleiner je nachdem, ob sich der Punkt in Sonnennähe oder -ferne befindet.
Es gilt somit für die Gezeitenkraft
Da der Radius der Erde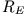 
klein im Vergleich mit dem Abstand Erde-Sonne ist, gilt in guter Näherung
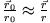an jedem Punkt der Erde und somit
Im Rahmen der gleichen Näherung approximiert man
(
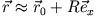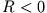: Punkt in Sonnennähe, 
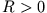: Punkt in
Sonnenferne) und erhält
Bemerkung:
In einer verallgemeinerten Form findet man die Gezeitenkraft überall in der Physik, wo wir es mit einem polarisierbaren Medium
zu tun haben.
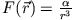ist die Kraft, die ein Dipol in einem Zentralkraftfeld spürt und 
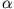(Polarisierbarkeit) ist die Fähigkeit eines Mediums sich in einen Dipol zu 'verformen'.
Analog erhält man eine Gezeitenkraft auf Massenelemente der Erde im System Erde-Mond (
)
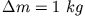Tabelle 6.2:
Größenvergleich zwischen Gezeitenkraft und Gravitation bezogen auf ein Massenelement
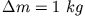auf der Erdoberfläche
(
,
,
,
,
).
|
|
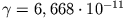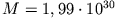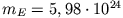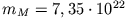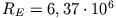Beispiele:
B6.5 Ebbe und Flut
Aus der Tabelle ersieht man, dass obwohl die Gravitation der Sonne 178 mal größer ist als die des Mondes, die Gezeitenkraft des Mondes an der
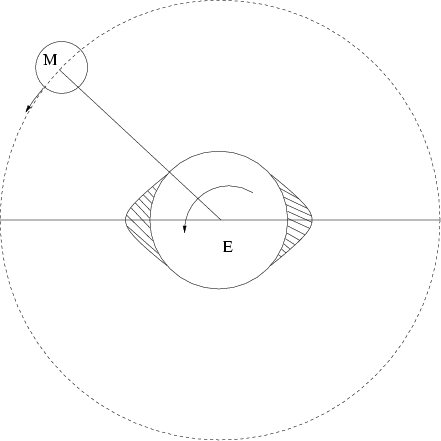
Abbildung 6.13:
Dephasierung durch Reibung der Flutberge an der Erdoberfläche.
 |
Erdoberfläche mehr als doppelt so groß wie die der Sonne ist. Daraus erklärt sich auch, warum der Mond für die Ebbe und Flut verantwortlich
ist. Die Gezeitenkraft des Mondes kann zwar die Erde nicht zerreißen, wohl aber die 'Wassermassen deformieren'. Die Erde dreht sich unter der
deformierten Wasserfläche durch: so entstehen Ebbe und Flut.
Schaut man genauer hin, so passiert noch mehr: Die Flutberge werden durch die Reibung an der rotierenden Erde etwas verschoben. Dadurch
bildet sich ein Winkel zwischen der Richtung der Flutberge und der Verbindungslinie Erde-Mond. Diese 'Dephasierung' bewirkt zweierlei: (i)
durch die Reibung zwischen Flutbergen und Erdoberfläche verlangsamt sich die Erdrotation und (ii) da die Massenverteilung des Wassers auf der
Erde elliptisch verformt ist, ist die Gravitationskraft auf den Mond keine reine Zentralkraft mehr. D.h. die Gravitation der Erde vor dem
Mond (bezogen auf die Bewegungsrichtung) ist stärker als 'hinter' dem Mond, was zu einer leichten Beschleunigung des Mondes auf seiner Bahn
führt. Erhöht sich jedoch die Bahngeschwindigkeit des Mondes, wird die Zentrifugalkraft größer und der Mond wird sich langsam auf einer
Spiralbahn von der Erde entfernen.
B6.6 Der Roche-Limes
Die Gezeitenkräfte können so stark werden, dass der Planet oder der Mond, der dem Gravitationszentrum zu nahe kommt, zerreißt.
Abbildung 6.14:
Zur Bestimmung eines minimalen Mondabstandes
 |
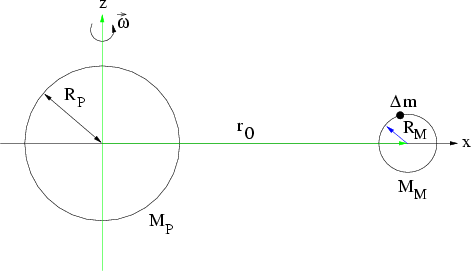Den
Mindestradius einer Kreisbahn
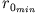unter dem ein Mond gerade noch durch seine eigene Gravitationskraft
zusammenhält erhält man aus der Bedingung, dass eine beliebige Masse 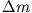an der Oberfläche des Mondes bezüglich Gravitation des
Mondes und Gezeitenkraft des Planeten in Gleichgewicht ist also
Nimmt man an, dass die Massen des Planeten und des Mondes homogen verteilt sind mit den Massendichten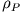 
bzw. 
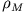, so
erhält man
für den Minimalabstand (Roche-Limes) des Mondes vom Planeten. Eine genauere Analyse, die die elliptische Deformation von Planet und Mond
mit einbezieht zeigt, dass
Für die Erde gilt
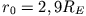, d.h. wenn der Mond der Erde näher käme, würden Felsen aus der Mondoberfläche herausgerissen werden.
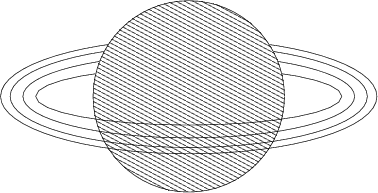
Abbildung 6.15:
Die Saturnringe liegen innerhalb des Roche-Limes
 |
Etwas ähnliches passierte mit dem Kometen Shoemaker-Levy (1994), der in der Nähe des Jupiters zerrissen wurde. Die Unterschreitung des
Roche-Limes ist auch die Ursache, dass die Materie der Saturnringe sich nicht zu einem Mond verdichten konnte.
M. Keim, H.J. Lüdde
