In Kapitel 1.5 haben wir gesehen, dass Inertialsysteme gleichwertig zur Beschreibung physikalischer Vorgänge sind (Relativitätsprinzip).
Hingegen treten in beschleunigten Bezugssystemen Scheinkräfte auf, die der Beschleunigung entgegen wirken.
Abbildung 6.1:
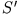 : Inertialsystem,
: Inertialsystem, 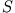 : beschleunigtes Bezugssystem
: beschleunigtes Bezugssystem
 |
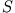 bewegt sich relativ zu einem Inertialsystem
bewegt sich relativ zu einem Inertialsystem 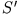 beschleunigt. Für jeden Punkt im Raum gilt
beschleunigt. Für jeden Punkt im Raum gilt
Um die Geschwindigkeitstransformation zu bestimmen, nehmen wir an, dass 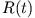 eine beschleunigte Translationsbewegung beschreibt. Das
System
eine beschleunigte Translationsbewegung beschreibt. Das
System 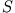 rotiere darüber hinaus (ohne Beschränkung der Allgemeinheit) um die z-Achse mit der Winkelgeschwindigkeit
rotiere darüber hinaus (ohne Beschränkung der Allgemeinheit) um die z-Achse mit der Winkelgeschwindigkeit
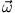 .
Wir wollen für den Augenblick die Translationsgeschwindigkeit vernachlässigen und annehmen,
.
Wir wollen für den Augenblick die Translationsgeschwindigkeit vernachlässigen und annehmen,
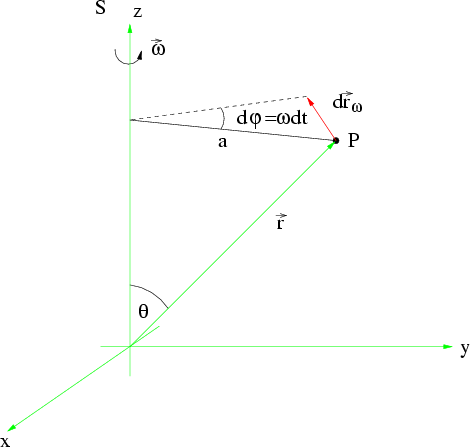
Abbildung 6.2:
Bewegung eines bezüglich des rotierenden Systems festen Raumpunktes
 |
dass 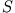 und
und 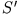 einen gemeinsamen Koordinatenursprung besitzen, also
einen gemeinsamen Koordinatenursprung besitzen, also 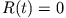 .
Sei
.
Sei 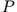 ein fester Punkt bezüglich des rotierenden Systems. Bezüglich des
Inertialsystems ändern sich die Komponenten des Punktes in der Zeit
ein fester Punkt bezüglich des rotierenden Systems. Bezüglich des
Inertialsystems ändern sich die Komponenten des Punktes in der Zeit 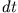 um den
Verschiebungsvektor
um den
Verschiebungsvektor 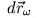 , also
, also
und somit
Bewegt sich der Massenpunkt zusätzlich im Raum mit der Geschwindigkeit
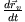 , so ergibt sich für die Verschiebung
, so ergibt sich für die Verschiebung
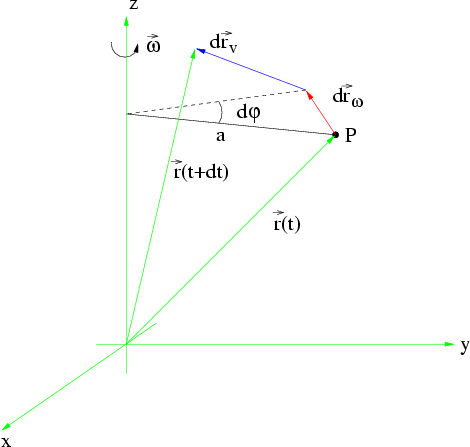
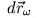 insgesamt
insgesamt
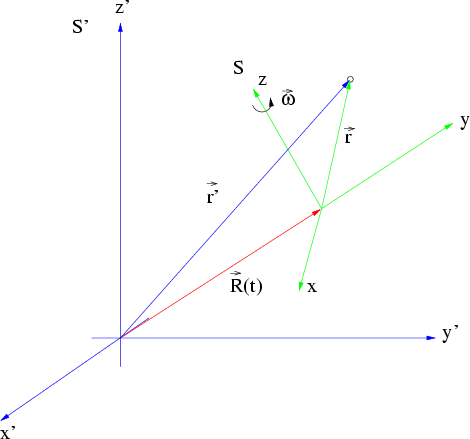
Abbildung 6.3:
Bewegter Massenpunkt im rotierenden Bezugssystem
 |
und
An dieser Stelle müssen wir unterscheiden zwischen der internen Bewegung des Massenpunktes relativ zum rotierenden System
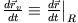 und der Gesamtbewegung gesehen aus dem Inertialsystem
und der Gesamtbewegung gesehen aus dem Inertialsystem
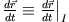 ,
von der aus man die Rotation des Systems
,
von der aus man die Rotation des Systems 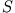 sieht
sieht
Diese Transformation zwischen Zeitableitungen von Vektoren des Inertial- und rotierenden Systems gilt allgemein, d.h. auch für die
Geschwindigkeit der Systeme
(Bemerkung:
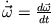 ist für beide Systeme gleich. Beweis:
ist für beide Systeme gleich. Beweis:
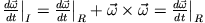 q.e.d.). D.h. wir erhalten für die Beschleunigung eines Massenpunktes
im rotierenden System (
q.e.d.). D.h. wir erhalten für die Beschleunigung eines Massenpunktes
im rotierenden System (
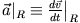 ) bezogen auf die Beschleunigung im Inertialsystem (
) bezogen auf die Beschleunigung im Inertialsystem (
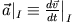 )
)
Kommt zusätzlich noch eine beschleunigte Translationsbewegung des Koordinatenursprungs von 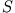 hinzu, erhält man
hinzu, erhält man
Der 'wahren Beschleunigung'
 gemessen im Inertialsystem wirken offenbar vier 'Schein-kräfte' entgegen:
(i)
gemessen im Inertialsystem wirken offenbar vier 'Schein-kräfte' entgegen:
(i)
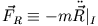 Trägheitskraft eines linear beschleunigten Bezugssystems (typisch in Aufzügen)
(ii)
Trägheitskraft eines linear beschleunigten Bezugssystems (typisch in Aufzügen)
(ii)
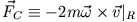 Corioliskraft, die auf einen im rotierenden Bezugssystem
bewegten Massenpunkt wirkt,
(iii)
Corioliskraft, die auf einen im rotierenden Bezugssystem
bewegten Massenpunkt wirkt,
(iii)
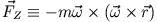 die Zentrifugalkraft und
(iv)
die Zentrifugalkraft und
(iv)
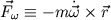 eine Scheinkraft, die durch eine ungleichmäßige
Rotationsgeschwindigkeit hervorgerufen
wird. Wir wollen uns im Folgenden auf die zwei Scheinkräfte beschränken, die wir in einem erdgebundenen Bezugssystem spüren: die
Zentrifugalkraft und die Corioliskraft.
eine Scheinkraft, die durch eine ungleichmäßige
Rotationsgeschwindigkeit hervorgerufen
wird. Wir wollen uns im Folgenden auf die zwei Scheinkräfte beschränken, die wir in einem erdgebundenen Bezugssystem spüren: die
Zentrifugalkraft und die Corioliskraft.
M. Keim, H.J. Lüdde
