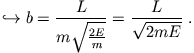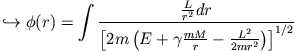Für die vereinfachte Planetenbewegung um die Sonne macht man folgende Annahmen:
- (i)
- Der Schwerpunkt des Systems Planet-Sonne befindet sich im Mittelpunkt der Sonne.
- (ii)
- Andere Himmelskörper haben keine Auswirkung auf die Bahn des betrachteten Planeten.
Abbildung 5.7:
Ekliptik (Erdbahn  Scheinbare Sonnenbahn)
Scheinbare Sonnenbahn)
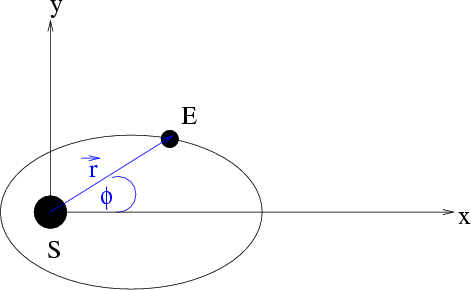 |
Da der Drehimpuls erhalten ist, müssen 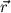 und
und 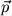 immer in derselben Ebene liegen, d.h. die Bewegung
eines ungestörten Himmelskörpers um die Sonne definiert eine Ebene. Aus diesem Grund wählen wir zur Beschreibung
der Planetenbahn ebene Polarkoordinaten
immer in derselben Ebene liegen, d.h. die Bewegung
eines ungestörten Himmelskörpers um die Sonne definiert eine Ebene. Aus diesem Grund wählen wir zur Beschreibung
der Planetenbahn ebene Polarkoordinaten
Da die Gravitationskraft konservativ ist, wird die mechanische Gesamtenergie ebenfalls zur
Erhaltungsgröße
Mit
erhält man schließlich für gegebenen Drehimpuls
einen Ausdruck für die Gesamtenergie, der nur vom momentanen Planetenabstand 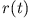 abhängt.
Die effektive potentielle Energie setzt sich zusammen aus der wahren potentiellen Energie und dem Zentrifugalpotential,
dem azimutalen Anteil der kinetischen Energie. Für einen gegebenen Drehimpuls
abhängt.
Die effektive potentielle Energie setzt sich zusammen aus der wahren potentiellen Energie und dem Zentrifugalpotential,
dem azimutalen Anteil der kinetischen Energie. Für einen gegebenen Drehimpuls 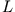 lassen sich die folgenden 4 Fälle unterscheiden:
lassen sich die folgenden 4 Fälle unterscheiden:
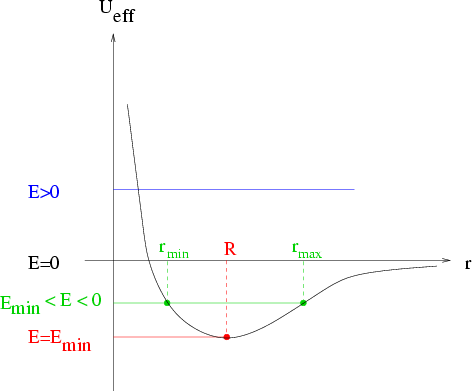
Abbildung 5.8:
Effektives Potential eines Planeten im Gravitationsfeld der Sonne
 |
- (i)
- .
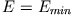 :
:
In diesem Fall hat der Planet einen konstanten Abstand von der Sonne
bewegt sich also auf einer Kreisbahn. Dann ist
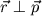 und somit
Die Umlaufzeit des Planeten beträgt
(wobei
und somit
Die Umlaufzeit des Planeten beträgt
(wobei
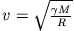 benutzt wurde).
benutzt wurde).
Somit haben wir für diesen Fall das 3. Keplersche Gesetz bestätigt.
- (ii)
- .
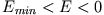 :
:
Für den allgemeinen Fall einer gebundenen Umlaufbahn erhalten wir zwei Umkehrpunkte
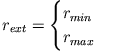 .
.
Dies führt zwangsläufig auf eine Ellipsenbahn mit der Halbachse 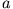 und der Exzentrizität
und der Exzentrizität 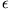 .
.
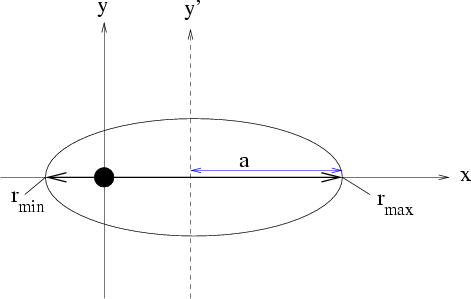
Abbildung 5.9:
Zusammenhang zwischen großer Halbachse 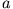 und den Umkehrpunkten
und den Umkehrpunkten 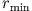 und
und 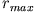 .
.
 |
Ansatz:
Vergleich mit 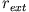 ergibt
ergibt
 und
und  bestätigen das 1. Keplersche Gesetz.
bestätigen das 1. Keplersche Gesetz.
- (iii)
- .
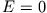 :
:
In diesem Fall ist der Körper gerade ungebunden und bewegt sich von
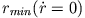 bis
bis
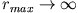 ,
so dass er bei
,
so dass er bei 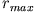 gerade keine kinetische Energie besitzt.
Die Exzentrizität ist
gerade keine kinetische Energie besitzt.
Die Exzentrizität ist
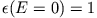 , was einer Parabel (siehe Kegelschnitte) entspricht.
Solche Körper gehören zum Sonnensystem, sind aber nicht gebunden.
, was einer Parabel (siehe Kegelschnitte) entspricht.
Solche Körper gehören zum Sonnensystem, sind aber nicht gebunden.
- (iv)
- .
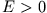 :
:
Diese Situation ist typisch für Körper, die nicht zu unserem Sonnensystem gehören,
also mit kinetischer Energie
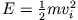 in das Gravitationsfeld der Sonne eintreten. Sie erreichen einen nächsten Abstand von der Sonne bei
und entfernen sich für immer aus dem Sonnensystem. Die Bahn ist eine Hyperbel
in das Gravitationsfeld der Sonne eintreten. Sie erreichen einen nächsten Abstand von der Sonne bei
und entfernen sich für immer aus dem Sonnensystem. Die Bahn ist eine Hyperbel
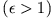 .
.
Dieser Fall entspricht einer dezentralen, elastischen Streuung mit Stoßparameter 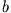
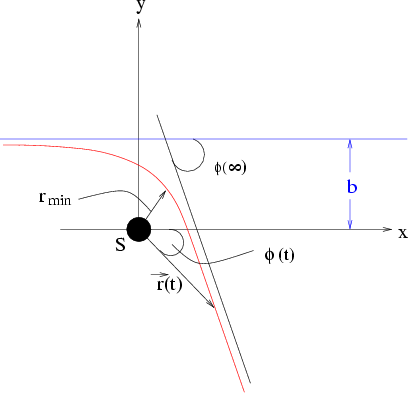
Abbildung 5.10:
Parameter eines dezentralen Streuproblems
 |
Will man die Trajektorie direkt berechnen, so geht man vom Energiesatz aus und erhält für die radiale Koordinate die DGL
bzw. für die Winkelkoordinate aus
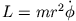 Da
Da
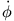 nicht von
nicht von 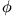 abängt, kann man die Winkeldgl. direkt integrieren, und zwar in folgender Form:
abängt, kann man die Winkeldgl. direkt integrieren, und zwar in folgender Form:
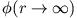 ist dann der Streuwinkel, unter dem der Körper den Einflussbereich des Potentials verlässt (Maple-Arbeitsblatt).
ist dann der Streuwinkel, unter dem der Körper den Einflussbereich des Potentials verlässt (Maple-Arbeitsblatt).
Zu Beginn der Diskussion haben wir gesehen, dass wegen der Drehimpulserhaltung die Planetenbewegung in der Ebene verlaufen muss.
Dazu berechnen wir nun das gerichtete Flächenelement 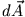 , das der Ortsvektor in der Zeit
, das der Ortsvektor in der Zeit 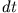 überstreicht
überstreicht
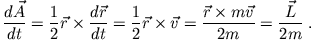
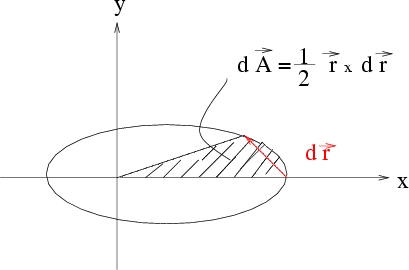
Da aber 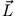 eine Erhaltungsgröße ist, muss auch
eine Erhaltungsgröße ist, muss auch
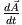 zeitlich konstant sein.
Somit ist auch das 2. Keplersche Gesetzt bestätigt.
zeitlich konstant sein.
Somit ist auch das 2. Keplersche Gesetzt bestätigt.
Abbildung 5.11:
Zum 2. Keplerschen Gesetz
 |
In Wirklichkeit ist leider alles viel komplizierter. Auf jeden Planeten wirkt nicht nur die Gravitationskraft der Sonne,
sondern auch die Kräfte aller anderen Planeten. Zwar ist, wie wir eingangs gesehen haben der Summendrehimpuls eine
Erhaltungsgröße, aber auf jeden einzelnen Planeten wirken die Zentralkräfte der anderen Planeten in verschiedenen Richtungen. Somit kommt es zu einem Austausch von Drehimpuls über die interplanetare Wechselwirkung. Damit sind auch die Planetenbahnen
komplizierter (nicht mehr in einer Ebene, keine reinen Ellipsenformen). Insbesondere ist das Mehrplanetensystem (ab 3 Planeten) nicht mehr integrabel - d.h. die Anzahl der Erhaltungsgrößen entspricht nicht mehr der Zahl der Freiheitsgrade. Solche Systeme
besitzen in der Regel chaotische Lösungen!
Das Applet Kepler's Gesetze löst das himmelsmechanische Einkörper-Problem für einen Satellit, der die Erde umkreist und präsentiert die Bewegung in Form einer Animation.
Zu sinnvoll gewählten Anfangsbedingungen für die Polarkoordinaten von Ort und Geschwindigkeit lassen sich die energetisch möglichen Keplerbahnen (Kreis, Ellipse, Parabel, Hyperbel) erzeugen. Der Betrag der Gravitationskraft ist dabei wie gewohnt F~(1/r)ß mit ß = 2. Was würde wohl passieren, wenn die Gravitationskraft mit einem leicht modifizierten Potenzgesetz abfallen würde, sagen wir ß = 2.05 oder ß = 1.95? Sie werden sehen, wie weittragend das so unscheinbare erste Gesetz von Kepler ist: Planeten (Satelliten) bewegen sich auf Ellipsen um die Sonne (Planeten)!
Zur Bestätigung des 2. und 3. Gesetzes von Kepler stehen alle Informationen in der Ausgabeleiste zur Verfügung: z.B.
a) bestimmen Sie die extremalen Abstände des Satelliten vom Erdmittelpunkt (Radius der Erde 6370km)
b) berechnen Sie daraus die Parameter der Ellipse (große Halbachse und Exzentrizität)
c) bestimmen Sie aus den Polarkoordinaten des Abstandes und der Geschwindigkeit des Satelliten bezogen auf den Erdmittelpunkt die vom Fahrstrahl überstrichene Fläche zum Nachweis des Flächensatzes
d) die Bahndaten zu verschiedenen Anfangsbedingungen erlauben schließlich die Überprüfung des 3. Gesetzes
U. Lechner, H.J. Lüdde

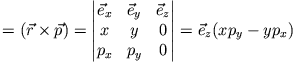
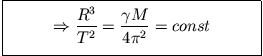
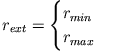 .
.
![]()