Ein Massenpunkt, der sich in 3 Dimensionen bewegt, besitzt bezogen auf ein bestimmtes Koordinatensystem einen
Drehimpuls
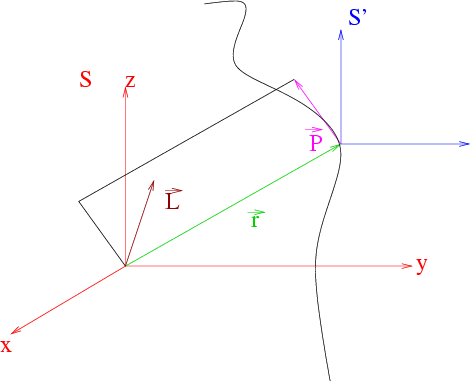
Abbildung 5.3:
Zur Definition des Drehimpulses
 |
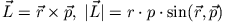
Der Betrag von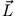 
entspricht dem von 
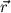und 
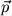aufgespannten Flächeninhalt, die Richtung von
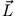ist senkrecht zu 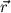und 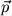in der Form, dass
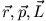ein Rechtssystem bilden.
Der Drehimpuls ist abhängig vom gewählten Koordinatensystem: in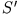 
z. B. ist 
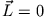(weil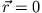 
).
Über Newton's BWGL ist einem Drehimpuls immer ein Drehmoment zugeordnet
Dies ist der Drehimpulssatz: ein Drehmoment bewirkt eine zeitliche Änderung des Drehimpulses.
Beispiele
B5.1 Wie öffnen Sie eine Tür: mit Kraft oder Drehmoment ?
B5.2 Wie üben Sie eine starke Kraft auf einen Körper aus ?
Abbildung 5.4:
Hebel
 |
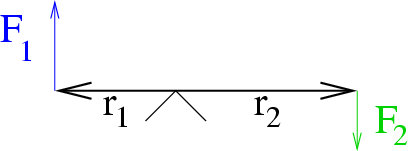Hebel: das Drehmoment auf beiden Seiten des gelagerten Balkens ist betragsmäßig gleich
(sonst würde der Balken brechen), d.h.
Insbesondere ist der Drehimpuls ein Integral der Bewegung für Systeme von Massenpunkten, auf die kein
äußeres Drehmoment wirkt: da wegen Newton's 3. Gesetz
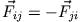, gilt für das interne
Drehmoment zwischen 2 Massenpunkten (i,j beliebig)
da
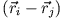parallel zu
ist.
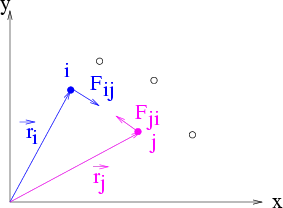
Abbildung 5.5:
Innere Drehmomente heben sich weg bei Systemen von Massenpunkten
 |
Somit gilt analog zum Impulssatz
die zeitliche Änderung des totalen Drehimpulses eines Systems von Massenpunkten
ist gleich der Summe der äußeren Drehmomente.
U. Lechner, H.J. Lüdde
