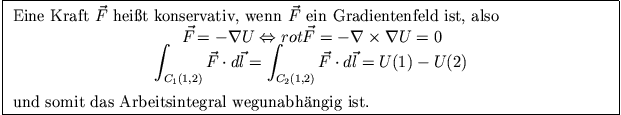Abbildung 5.1:
Zum Begriff der Arbeit
 |
- Eindimensionale Bewegung
Die infinitesimale Arbeit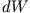 
, die von einer Kraft 
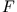entlang der Trajektorie
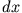eines Massenpunktes aufgebracht wird, ist
- Dreidimensionale Bewegung
Die infinitesimale Arbeit, die entlang einer 3 dim. Trajektorie aufgebracht wird, ergibt sich aus der
Kraftkomponente entlang der Trajektorie (Projektion von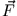 
auf Trajektorienelemente 
)
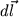Die integrale Arbeit entlang einer Trajektorie C (Contour) zwischen den Punkten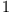 
und 
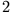ist dann
Mathematisch entspricht die Arbeit einem Kurvenintegral (2. Art) über das Vektorfeld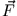
(Summation aller infinitesimalen Skalarprodukte
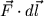entlang einer Trajektorie).
Im Gegensatz zu eindimensionalen Bewegungsformen stellt sich sofort die Frage, ob die Arbeit von
der Form der Trajekorie
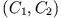abhängt?
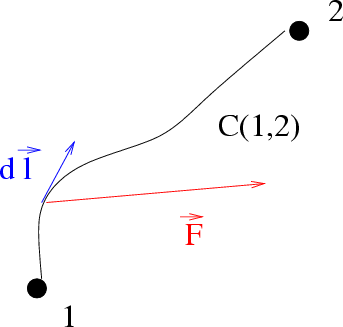
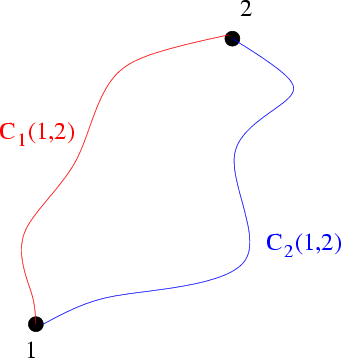
Abbildung 5.2:
Arbeitsintegral entlang verschiedener Wege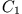 
und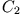 
 |
In diesem Zusammenhang haben wir den Begriff ''konservative Kraft''eingeführt: eine
eindimensionale Kraft heißt konservativ, wenn sie durch Ortsableitung aus einer
Potentialfunktion herleitbar ist:
Für solche Kräfte ist das Arbeitsintegral
gleich der Potentialdifferenz zwischen Anfangs- und Endpunkt der Bewegung.
Übertragen auf 3 dim. Bewegungsformen würde man eine Kraft 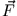dann
konservativ nennen, wenn gilt:
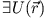, so dass
Dann gilt für das Arbeitsintegral
dass es sich als Integral über das totale Differential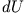 
der Potentialfunktion schreiben lässt und somit 
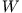nur von
Anfangs- und Endpunkt der Bewegung abhängt, aber nicht von der Form des Weges dazwischen.
Somit haben wir folgende äquivalente Aussagen:
Speziell zeigt sich die Wegunabhängigkeit des Arbeitsintegrals an einer geschlossenen Trajektorie
Benutzt man Newton's Bewegungsgleichung in der Form
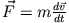, so erhält man wie im eindimensionalen Fall
dass mit einer erbrachten Arbeit entlang einer Trajektorie immer eine Änderung der kinetischen Energie verbunden ist.
Für konservative Systeme haben wir somit die Aussage
die totale mechanische Energie ist eine Erhaltungsgröße.
U. Lechner, H.J. Lüdde
