4.5 Bewegung einer Rakete

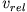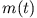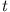Eine Rakete bewegt sich im kräftefreien Raum unter dem Einfluss ihres Triebwerkes: mit hoher Geschwindigkeit werden Antriebsgase relativ zur Rakete ausgestoßen und beschleunigen somit das Raumschiff. Sei die Masse der Rakete (Treibstoff, Raketenhülle und Nutzlast) zur Zeit und 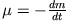der konstante Gasausstoß pro Zeiteinheit (Beachte: die Masse der Rakete nimmt ab, deshalb ist 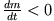und damit 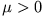). Die Austrittsgeschwindigkeit der Gase von der Erde (Laborsystem) aus betrachtet, ist

Dabei ist 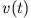die momentane Geschwindigkeit der Rakete und 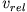, wie oben erwähnt, die konstante Austrittsgeschwindigkeit der Gase relativ zur Rakete. Da keine äußeren Kräfte wirken, gilt für das System Rakete und ausströmende Gase die Impulserhaltung

Dabei setzt sich der Impuls des Systems zur Zeit zusammen aus dem Impuls der Rakete zur Zeit 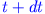und dem Impuls der ausströmenden Gase. Ausmultipliziert ergibt sich

Beachtet man, dass wegen der Konstanz von

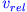
gilt, so ergibt sich

Wir erhalten somit eine Differentialgleichung für v(m) bzw. m(v), die wir mit Hilfe der Separation der Variablen lösen können (wähle als Anfangsbedingung v(0)=0)

Sei nun T die Brenndauer der Rakete, also die Zeit, in der aller Treibstoff verbraucht ist. Dann setzt sich m(T) aus der Masse der Nutzlast und der Raketenhülle zusammen.

B4.4 Endgeschwindigkeit der Rakete

Nutzlast und Raketenhülle betragen 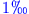der Startmasse m(0). Welche Endgeschwindigkeit erreicht die Rakete?

Beachten Sie: die Endgeschwindigkeit ist proprotional zur Austrittsgeschwindigkeit der Gase. Bei heutigen Raketenmotoren ist 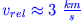, die theoretische Endgeschwindigkeit somit .

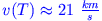B4.5 Treibstoffmenge der Rakete

Sei 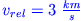. Wie groß muss die Treibstoffmenge sein, um eine Nutzlast von 1 kg auf 1% der Lichtgeschwindigkeit zu beschleunigen? ( )
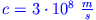Aus

erhält man

Die Menge des benötigten Raketentreibstoffes überschreitet damit die Masse des Universums.
An den Beispielen erkennt man, dass die Endgeschwindigkeit einer Rakete wesentlich durch die Austrittsgeschwindigkeit der Antriebsgase 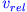bestimmt ist. Raketen für interplanetare Raumflüge werden sicher nicht mit chemischen Raketenmotoren ( 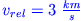) ausgerüstet werden, sondern mit Ionentriebwerken. Eine Spannung von 25000 V beschleunigt ein Proton auf etwa 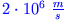. Die technische Herausforderung besteht in der Bereitstellung der benötigten Ionendichten.