Ist die Kraft zwischen den zwei Massenpunkten nicht konservativ sondern dissipativ, so geht mechanische Energie durch Reibung verloren.
B4.3 Ballistisches Pendel
Bestimme die Geschwindigkeit eines Geschosses, das in einem frei aufgehängten Sandsack aufgefangen wird.
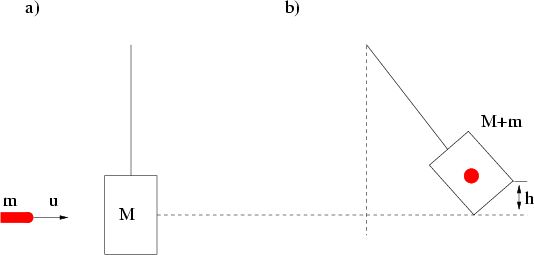
Abbildung 4.6:
Messung von 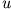 aus der Höhe
aus der Höhe 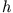 des ballistischen Pendels. a) vor dem Stoß b) nachdem das Geschoss vom Sandsack
des ballistischen Pendels. a) vor dem Stoß b) nachdem das Geschoss vom Sandsack 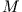 eingefangen wurde.
eingefangen wurde.
 |
Es gilt Impulserhaltung für das abgeschlossene System: Da das Pendel vor dem Stoß in Ruhe ist, gilt
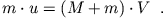 |
(4.9) |
Dabei ist 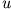 die gesuchte Geschwindigkeit des Geschosses und
die gesuchte Geschwindigkeit des Geschosses und 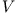 die Geschwindigkeit des Pendels der Masse
die Geschwindigkeit des Pendels der Masse 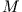 , nachdem es das Geschoss
eingefangen hat. Nach dem Stoß gilt Energieerhaltung für das frei schwingende Pendel, also
, nachdem es das Geschoss
eingefangen hat. Nach dem Stoß gilt Energieerhaltung für das frei schwingende Pendel, also
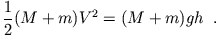 |
(4.10) |
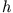 ist die Höhe der Pendelmasse im Umkehrpunkt. Für den Stoß selbst gilt keine Energieerhaltung, da die Kugel in der Pendelmasse abgebremst
wird und dabei die Reibungsenergie
ist die Höhe der Pendelmasse im Umkehrpunkt. Für den Stoß selbst gilt keine Energieerhaltung, da die Kugel in der Pendelmasse abgebremst
wird und dabei die Reibungsenergie 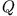 abgibt
abgibt
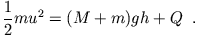 |
(4.11) |
Aus (4.10) folgt
Einsetzen in (4.9) liefert
Wenn man aus dem Maximalausschlag des Pendels 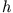 bestimmt, erhält man die Geschwindigkeit des Projektils.
bestimmt, erhält man die Geschwindigkeit des Projektils.
Wie groß ist dann die Reibungsenergie 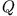 ? Aus (4.11) erhält man
? Aus (4.11) erhält man
Der Anteil der Reibungsenergie an der ursprünglichen kinetischen Energie der Kugel beträgt
Arbeitsblatt: Ballistisches Pendel
M. Keim, H.J. Lüdde

