Ist die interne Wechselwirkung
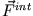 zwischen den Massenpunkten konservativ, so gilt zusätzlich zur Impulserhaltung auch die
Energieerhaltung, d.h. die Summen der kinetischen Energien außerhalb der Wechselwirkunsgzone vor und nach dem Stoß sind identisch
zwischen den Massenpunkten konservativ, so gilt zusätzlich zur Impulserhaltung auch die
Energieerhaltung, d.h. die Summen der kinetischen Energien außerhalb der Wechselwirkunsgzone vor und nach dem Stoß sind identisch
Solche Streuvorgänge nennt man elastische Stöße.
Beispiele:
B4.1 Eindimensionaler elastischer Stoß (zentraler Stoß)
Gegeben sind die Anfangsgeschwindigkeiten 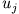 zweier Massenpunkte. Bestimme die Endgeschwindigkeiten
zweier Massenpunkte. Bestimme die Endgeschwindigkeiten 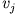 nach einem elastischen Stoß.
Die Energieerhaltung liefert
nach einem elastischen Stoß.
Die Energieerhaltung liefert
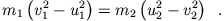 |
(4.3) |
Impulserhaltung
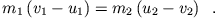 |
(4.4) |
Das Verhältnis von (4.3) zu (4.4) ergibt nach dem 3. binomischen Lehrsatz
Man sieht, dass die Relativgeschwindigkeit im zentralen elastischen Stoß die Richtung umkehrt. Aus (4.5) und (4.4) folgt
Wir betrachten einige Spezialfälle für 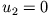 (ruhendes Target (Zielmasse)):
(ruhendes Target (Zielmasse)):
- (i)
- .
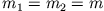 :
:
In diesem Fall ist 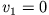 und
und 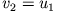 . D.h. die kinetische Energie der Projektilmasse
. D.h. die kinetische Energie der Projektilmasse 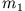 wird vollständig auf die Targetmasse
wird vollständig auf die Targetmasse 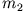 übertragen.
übertragen.
- (ii)
- .
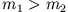 :
:
Es gilt
Beide Massen fliegen in positiver Richtung weiter mit 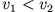 .
.
- (iii)
- .
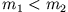 :
:
Beide Massen bewegen sich nach dem Stoß in entgegengesetzter Richtung mit den Geschwindigkeiten
Für den Spezialfall
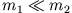 ergibt sich dann
ergibt sich dann
(Bsp.: Schuss eines Balles (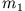 ) gegen eine Wand (
) gegen eine Wand (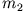 )).
)).
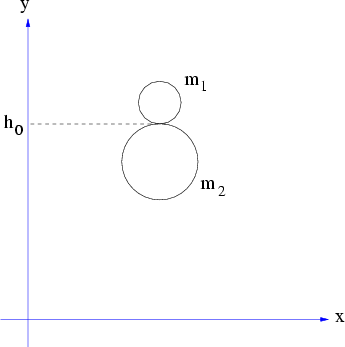
B4.2 Elastischer Stoß zweier fallender Bälle unterschiedlicher Masse
Ein Tischtennisball der Masse 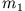 und ein Hartgummiball der Masse
und ein Hartgummiball der Masse 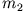 fallen aus einer Höhe
fallen aus einer Höhe 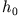 senkrecht nach unten.
senkrecht nach unten.
Abbildung 4.5:
Ballspiele
 |
Welche Höhe
erreicht der Tischtennisball nach dem Auftreffen maximal?
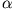 )
)- Im ersten Schritt bestimmen wir die Auftreffgeschwindigkeit der Bälle aus dem Energiesatz
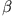 )
)- Die zweite Phase ist bestimmt durch zwei kurz aufeinanderfolgende elastische Stöße
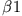 )
)- .
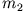 trifft elastisch auf den Boden (
trifft elastisch auf den Boden (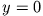 ) auf und kehrt seinen Impuls um.
) auf und kehrt seinen Impuls um.
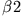 )
)- .
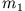 und
und 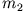 stoßen zusammen (fast am Boden, wo sie keine potentielle Energie besitzen), so dass
stoßen zusammen (fast am Boden, wo sie keine potentielle Energie besitzen), so dass 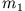 eine
Geschwindigkeit nach oben erhält.
eine
Geschwindigkeit nach oben erhält.
Daraus erhält man die Geschwindigkeit der Massen vor ihrem Zusammenstoß (wegen 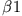 )
)
und die Geschwindigkeiten 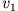 und
und 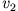 nach dem Stoß aus Impuls- und Energieerhaltung
nach dem Stoß aus Impuls- und Energieerhaltung
Zur Bestimmung der Flughöhe benutzen wir wieder die Energieerhaltung für die Masse 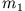 (senkrechter Wurf nach oben)
(senkrechter Wurf nach oben)
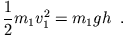 |
(4.8) |
Damit ergibt sich aus (4.6)
und Einsetzen in (4.7)
Aus (4.8) erhält man mit 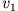
Die maximal erreichbare Höhe erhalten wir für
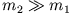 , so dass wir
, so dass wir 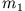 gegenüber
gegenüber 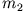 vernachlässigen können, also
vernachlässigen können, also
Das Arbeitsblatt Elastischer Stoß unter dem Einfluss der Gravitation erlaubt es Ihnen, dieses Beispiel noch einmal interaktiv nachzuempfinden.
M. Keim, H.J. Lüdde