Wir betrachten zwei Massenpunkte in einem äußeren Kraftfeld. Die wirksamen Kräfte ergeben sich aus der internen Wechselwirkung zwischen den Massenpunkten und den externen Kräften
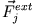 .
.
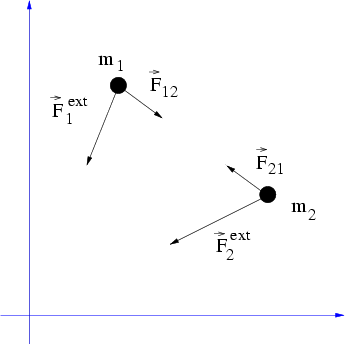
Abbildung 4.2:
Bewegung von zwei gravitativ wechselwirkenden Massenpunkten in einem äußeren Kraftfeld.
 |
Damit lauten die
Bewegungsgleichungen
wobei für die internen Kräfte nach Newtons's 3. Gesetz (actio gleich reactio) gilt
Addiert man die beiden Bewegungsgleichungen, so erhält man
Im nächsten Schritt führen wir eine neue Koordinate ein, den Schwerpunkt:
und erhalten für die addierten Bewegungsgleichungen
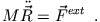 |
(4.1) |
D.h. das Gesamtsystem bewegt sich wie ein fiktiver Massenpunkt der Masse 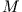 am Ort
am Ort 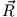 im externen Kraftfeld
im externen Kraftfeld
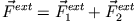 .
.
Bemerkungen
- (i)
- Man nennt das System von Massenpunkten isoliert oder abgeschlossen, wenn keine äußeren Kräfte wirken, also
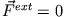 . Dann ist
. Dann ist
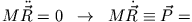 const. const. |
|
der Summenimpuls
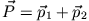 des Systems (Schwerpunktimpuls) eine Erhaltungsgröße (Impulserhaltung).
des Systems (Schwerpunktimpuls) eine Erhaltungsgröße (Impulserhaltung).
- (ii)
- Die externe Kraft
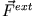 ist im Allgemeinen keine Zentralkraft (siehe Abb. 4.2: die Überlagerung von
ist im Allgemeinen keine Zentralkraft (siehe Abb. 4.2: die Überlagerung von
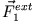 und
und
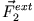 ist vom Schwerpunkt aus gesehen nicht auf das äußere Kraftzentrum gerichtet).
ist vom Schwerpunkt aus gesehen nicht auf das äußere Kraftzentrum gerichtet).
- (iii)
- Einen Sonderfall stellen konstante externe Kräfte dar (z.B. erdnahe Gravitation). In diesem Fall gilt
Der Schwerpunkt des Systems bewegt sich wie ein Massenpunkt der Masse 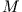 mit konstanter Beschleunigung.
mit konstanter Beschleunigung.
M. Keim, H.J. Lüdde
