Das einfachste Beispiel für einen nichtlinearen Oszillator ist das mathematische Pendel.
An einem masselosen unendlich steifen Faden der Länge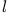 
hängt ein Massenpunkt der Masse
m.
Abbildung 3.15:
Freies mathematisches Pendel
 |
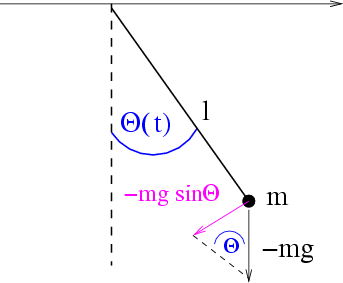Der bewegungsrelevante Anteil der Gravitationskraft ist die nichtlineare Rückstellkraft
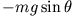, so dass man als Bewegungsgleichung für das freie mathematische Pendel
erhält
Darüber hinaus kann man verschiedene Formen eines getriebenen Pendels realisieren:
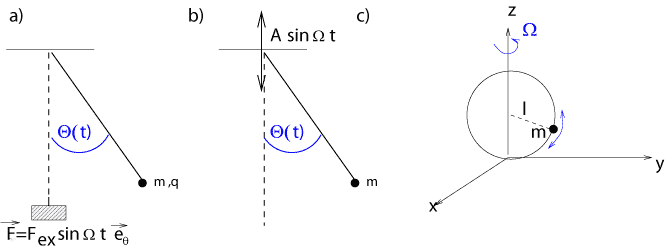
Abbildung 3.16:
Getriebene Pendel. a)Die Masse ist geladen und wird durch ein elektrisches Wechselfeld der Frequenz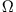 
entlang der Kreisbahn angestoßen. b)Das parametrisch angeregte Pendel schwingt mit der Freq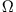uenz in der
Aufhängung. c)Eine Perle bewegt sich reibungsfrei auf einem rotierenden (Kreisfrequenz ),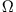
kreisförmigen Draht.
 |
Die entsprechenden Bewegungsgleichungen lauten in ihrer kanonischen Form
- zu a)
wobei der Reibungsterm nach Stokes proportional zur Winkelgeschwindigkeit
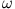angenommen wird.
- zu b)
- zu c)
Wir wollen uns mit den Konsequenzen einer nichtlinearen Rückstellkraft am Beispiel des getriebenen
Pendels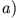 
auseinandersetzen. Parallel zum folgenden Text können Sie sich
mit Hilfe des Applets zum mathematischen Pendel mit den vielfältigen
Bewegungsformen vertraut machen. Ein weiteres Applet zum Beispiel c) soll Sie zur Untersuchung eines "spontanen
Symmetriebruches" einladen.
U. Lechner, H.J. Lüdde
