Abbildung 3.13:
Oszillatorkette
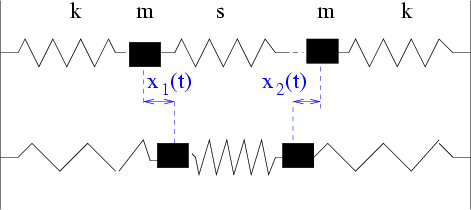 |
Ein System von zwei gekoppelten Oszillatoren wird beschrieben durch die Bewegungsgleichung
Daraus ergibt sich mit
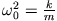
ein gekoppeltes System aus zwei Differentialgleichungen 2. Ordnung.
Mit Hilfe der Substitution
lassen sich die Differentialgleichungen entkoppeln. Einsetzen ergibt
Durch Addition
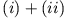 und Subtraktion
und Subtraktion 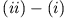 erhält man
erhält man
Die Oszillatoren entkoppeln in den neuen Koordinaten 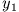 und
und 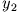 . Man bezeichnet sie als
die Normalschwingungen (Normalmoden) des Systems. Die Lösungen sind
. Man bezeichnet sie als
die Normalschwingungen (Normalmoden) des Systems. Die Lösungen sind
mit den beiden charakteristischen Frequenzen 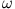 und
und 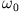 .
Um die Normalmoden
.
Um die Normalmoden 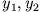 besser interpretieren zu können,
transformieren wir in die ursprünglichen Koordinaten zurück
besser interpretieren zu können,
transformieren wir in die ursprünglichen Koordinaten zurück
Mit bestimmten Anfangsbedingungen 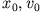 können wir die folgenden Fälle unterscheiden
können wir die folgenden Fälle unterscheiden
- (a)
- .
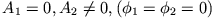 :
:
Beide Oszillatoren schwingen in Phase mit gleicher Amplitude und der natürlichen Frequenz 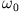 .
D.h. die mittlere Feder wird nicht aus ihrer entspannten Lage ausgelenkt. Dies entspricht
der Normalschwingung
.
D.h. die mittlere Feder wird nicht aus ihrer entspannten Lage ausgelenkt. Dies entspricht
der Normalschwingung 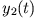 .
.
- (b)
- .
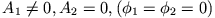 :
:
Die beiden Oszillatoren schwingen in Gegenphase
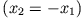 mit der größeren Frequenz
mit der größeren Frequenz
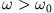 .
In dieser Normalschwingung
.
In dieser Normalschwingung 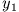 wird nun auch die mittlere Feder wirksam: dies erklärt die größere Frequenz.
wird nun auch die mittlere Feder wirksam: dies erklärt die größere Frequenz.
- (c)
- .
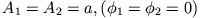 :
:
Umformung ergibt
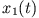 und
und 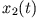 oszillieren phasenverschoben mit der Frequenz
oszillieren phasenverschoben mit der Frequenz
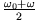 .
Die Amplitude wird moduliert mit der kleineren Frequenz
.
Die Amplitude wird moduliert mit der kleineren Frequenz
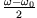 (Beatfrequenz).
Mit dieser Modulationsfrequenz tauschen die beiden Oszillatoren Energie aus.
Ist die Kopplung zwischen den Oszillatoren groß, gilt
(Beatfrequenz).
Mit dieser Modulationsfrequenz tauschen die beiden Oszillatoren Energie aus.
Ist die Kopplung zwischen den Oszillatoren groß, gilt
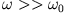 , erfolgt der
Energieaustausch schnell.
, erfolgt der
Energieaustausch schnell.
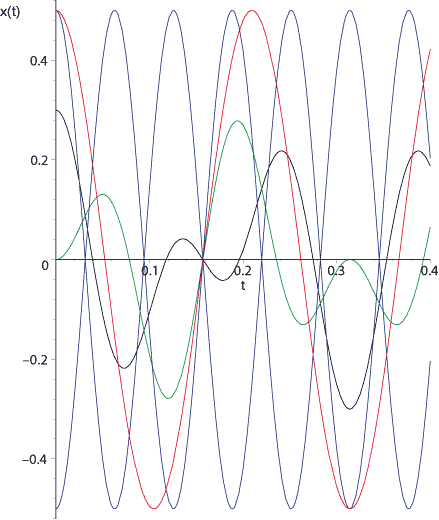
Abbildung:
Energieaustausch im gekoppelten Oszillator. Fall a):rot ; Fall b):blau ; Fall c):grün und schwarz
 |
Das Applet Normalschwingungen in einem gekoppelten Oszillator erlaubt Ihnen, für voreingestellte Anfangsbedingungen die besprochenen Bewegungsformen zu simulieren.
U. Lechner, H.J. Lüdde

