Abbildung 3.10:
Getriebener harmonischer Oszillator
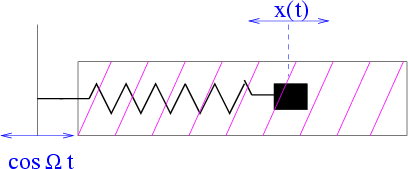 |
Treibt man den harmonischen Oszillator durch eine äußere harmonische Kraft an, so hat man
die Bewegungsgleichung zu lösen
Dabei handelt es sich um eine lineare inhomogene Differentialgleichung 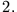 Ordnung mit konstanten Koeffizienten.
Eine allgemeine Lösung erhält man durch Superposition der allgemeinen Lösung
Ordnung mit konstanten Koeffizienten.
Eine allgemeine Lösung erhält man durch Superposition der allgemeinen Lösung 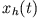 der zugehörigen
homogenen Differentialgleichung
der zugehörigen
homogenen Differentialgleichung
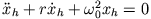 und einer speziellen Lösung
und einer speziellen Lösung
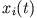 der inhomogenen Differentialgleichung (Partikulärintegral), also
Wir machen den Ansatz
und müssen zeigen, dass B und
der inhomogenen Differentialgleichung (Partikulärintegral), also
Wir machen den Ansatz
und müssen zeigen, dass B und 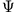 so bestimmt werden können, dass der Ansatz die Bewegungsgleichung erfüllt.
Durch Einsetzen erhält man
so bestimmt werden können, dass der Ansatz die Bewegungsgleichung erfüllt.
Durch Einsetzen erhält man
Da  eine Lösung der homogenen Gleichung ist, folgt mit Hilfe der Additionstheoreme
eine Lösung der homogenen Gleichung ist, folgt mit Hilfe der Additionstheoreme
Diese Bedingung muss für beliebige Zeiten erfüllt werden. Da
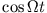 und
und
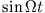 linear unabhängig
sind ist dies nur möglich wenn die Ausdrücke in den Klammern 0 sind, also
linear unabhängig
sind ist dies nur möglich wenn die Ausdrücke in den Klammern 0 sind, also
Aus 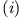 erhält man mit Division durch
erhält man mit Division durch 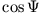 eine Bestimmung der Phase
eine Bestimmung der Phase
Die Amplitude erhält man,indem man (i) und (ii) quadriert und das Ergebnis addiert
Damit haben wir als allgemeine Lösung des getriebenen harmonischen Oszillators
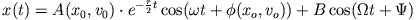 |
(3.4) |
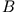 und
und 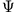 sind durch die Parameter der Differentialgleichung festgelegt,
sind durch die Parameter der Differentialgleichung festgelegt, 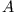 und
und 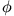 müssen
über die Anfangsbedingungen
müssen
über die Anfangsbedingungen 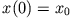 und
und
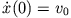 bestimmt werden.
Wir sehen, dass die Lösung (3.4) zwei typische Verhaltensmuster aufweist: (i) für kleine Zeiten zeigt sich
ein vorübergehendes Einschwingverhalten durch die Überlagerung von
bestimmt werden.
Wir sehen, dass die Lösung (3.4) zwei typische Verhaltensmuster aufweist: (i) für kleine Zeiten zeigt sich
ein vorübergehendes Einschwingverhalten durch die Überlagerung von
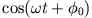 und
und
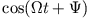 . (ii) für große Zeiten klingt die Amplitude des ersten Terms exponentiell ab,
so dass der Oszillator vollständig durch die harmonische Antriebskraft ''versklavt'' wird.
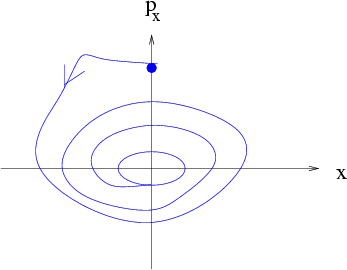
Im Phasenraum entspricht die zeitlich asymptotische Lösung einer Ellipse.
. (ii) für große Zeiten klingt die Amplitude des ersten Terms exponentiell ab,
so dass der Oszillator vollständig durch die harmonische Antriebskraft ''versklavt'' wird.
Im Phasenraum entspricht die zeitlich asymptotische Lösung einer Ellipse.
Abbildung 3.11:
Phasenraumtrajektorie des getriebenen Oszillators.
 |
Da jede Lösung (zu gegebenen
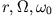 ) zu einer beliebigen Anfangsbedingung
) zu einer beliebigen Anfangsbedingung 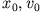 gegen die
selbe asymptotische Lösung konvergiert, nennt man sie Grenzkreislösung. Sie entspricht einem Attraktor der
Dimension
gegen die
selbe asymptotische Lösung konvergiert, nennt man sie Grenzkreislösung. Sie entspricht einem Attraktor der
Dimension 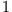 . Amplitude und Phase der Grenzkreislösung hängen von den Parametern der Differentialgleichung ab.
. Amplitude und Phase der Grenzkreislösung hängen von den Parametern der Differentialgleichung ab.
Man sieht, dass die Amplitude maximal wird, wenn die Erregerfrequenz 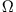 der Eigenfrequenz des freien
Oszillators
der Eigenfrequenz des freien
Oszillators 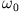 entspricht. In diesem Fall nimmt die Phase
entspricht. In diesem Fall nimmt die Phase 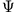 den Wert
den Wert 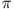 /2 an.
Dieses Verhalten bezeichnet man als Resonanz. Abhängig vom Reibungskoeffizient kann die Amplitude
sehr groß werden und den Oszillator - z.B. ein Hochhaus oder eine Brücke - zu so starken
Schwingungen anregen, dass er zerstört wird (Resonanzkatastrophe).
/2 an.
Dieses Verhalten bezeichnet man als Resonanz. Abhängig vom Reibungskoeffizient kann die Amplitude
sehr groß werden und den Oszillator - z.B. ein Hochhaus oder eine Brücke - zu so starken
Schwingungen anregen, dass er zerstört wird (Resonanzkatastrophe).
Zum Abschluss der Diskussion über verschiedene Bewegungsformen des harmonischen Oszillators, können Sie den Stoff mit Hilfe eines Arbeitsblattes und eines Applets zum schweren Feder Pendel vertiefen.
U. Lechner, H.J. Lüdde

![]() eine Lösung der homogenen Gleichung ist, folgt mit Hilfe der Additionstheoreme
eine Lösung der homogenen Gleichung ist, folgt mit Hilfe der Additionstheoreme
![]() und
und
![]() linear unabhängig
sind ist dies nur möglich wenn die Ausdrücke in den Klammern 0 sind, also
linear unabhängig
sind ist dies nur möglich wenn die Ausdrücke in den Klammern 0 sind, also
![]() erhält man mit Division durch
erhält man mit Division durch ![]() eine Bestimmung der Phase
eine Bestimmung der Phase
![]() der Eigenfrequenz des freien
Oszillators
der Eigenfrequenz des freien
Oszillators ![]() entspricht. In diesem Fall nimmt die Phase
entspricht. In diesem Fall nimmt die Phase ![]() den Wert
den Wert ![]() /2 an.
Dieses Verhalten bezeichnet man als Resonanz. Abhängig vom Reibungskoeffizient kann die Amplitude
sehr groß werden und den Oszillator - z.B. ein Hochhaus oder eine Brücke - zu so starken
Schwingungen anregen, dass er zerstört wird (Resonanzkatastrophe).
/2 an.
Dieses Verhalten bezeichnet man als Resonanz. Abhängig vom Reibungskoeffizient kann die Amplitude
sehr groß werden und den Oszillator - z.B. ein Hochhaus oder eine Brücke - zu so starken
Schwingungen anregen, dass er zerstört wird (Resonanzkatastrophe).