3.3 Der Phasenraum

Bisher haben wir die kinematischen Größen Ort und Impuls (Geschwindigkeit) immer als Funktion der Zeit betrachtet. Die Bewegung eines Massenpunktes ist vollständig bestimmt, wenn wir zu jeder Zeit Ort und Impuls des Massenpunktes angeben können. Am besten realisiert man diese Forderung in einer Darstellung, in der alle Orts- und Impulskomponenten eines Massenpunktes zusammengefasst werden: der Phasenraum.

Abbildung 3.9: Phasenraumdarstellung des harmonischen Oszillators. a)Die Phasenraumtrajektorie eines freien Oszillators ist eine Ellipse der Form: 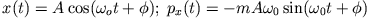. Der Koordinatenursprung ist die stabile Punktlösung, die man erhält, wenn man den Oszillator mit Anfangsgeschwindigkeit 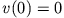in seinen Gleichgewichtszustand 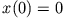versetzt! b)Die Phasenraumtrajektorie des gedämpften Oszillators beschreibt eine Spirale mit der Parameterdarstellung .

Bemerkungen:

(i)

Eine Gleichgewichtslösung wird im Phasenraum als Punkt dargestellt. Der Punkt 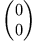ist für den harmonischen Oszillator eine stabile Punktlösung.

(ii)

Der Teilraum des Phasenraums, in dem Anfangsbedingungen liegen, deren zugehörige Trajektorien gegen die selbe stabile Punktlösung konvergieren, heißt Attraktorbecken der Punktlösung. Entsprechend nennt man eine stabile Punktlösung einen Attraktor der Dimension 0.

(iii)

Die Phasenraumtrajektorie bestimmt den ''Lebensraum'' eines Massenpunktes zu allen Zeiten: es können nur die Punkte im Phasenraum erreicht werden, die zur Trajektorie gehören.

(iv)

Das Existenz- und Eindeutigkeitstheorem für Systeme autonomer (nicht explizit zeitabhängiger) Differentialgleichungen besagt, dass die Lösung eine eindeutige Funktion der Anfangsbedingungen ist, wenn die Differentialgleichung eine Lipschitzbedingung erfüllt (grob entspricht dies der Bedingung, dass die ''rechte Seite'' der Differentialgleichung stetig ist). In diesem Sinne dürfen sich zwei Phasenraumtrajektorien der selben Differentialgleichung zu verschiedenen Anfangsbedingungen nicht schneiden. Würde man nämlich die Anfangsbedingungen auf den Schnittpunkt legen, wäre die Eindeutigkeit nicht erfüllbar. Insbesondere darf sich eine Trajektorie nicht selbst schneiden. (Beachte: Eine Differentialgleichung 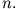Ordnung lässt sich immer in ein System aus 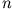Differentialgleichungen 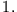Ordnung zerlegen!).