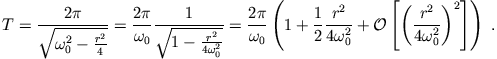Die Bewegungsgleichung des gedämpften Oszillators lautet
Mit dem Ansatz
erhält man die charakteristische Gleichung
Bestimmung der beiden möglichen Exponenten
Die allgemeine Lösung lautet dann
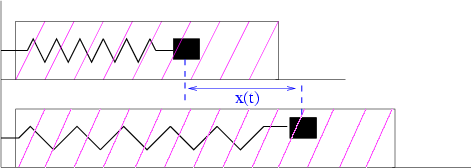
Abbildung 3.5:
Realisierung eines Stoßdämpfers. Reibung durch Viskosität der Kolbenflüssigkeit.
 |
Zur weiteren Diskussion wollen wir die folgenden Fälle unterscheiden
- (1)
- Überdämpfter Fall:
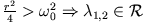
In diesem Fall sind die Exponenten reell und negativ. Man erhält für 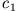 und
und 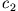 aus den
Anfangsbedingungen
aus den
Anfangsbedingungen
Abbildung 3.6:
Überdämpfter oder Kriechfall für  und
und  .
.
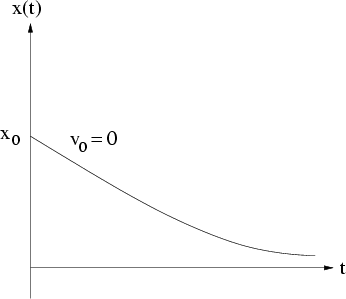 |
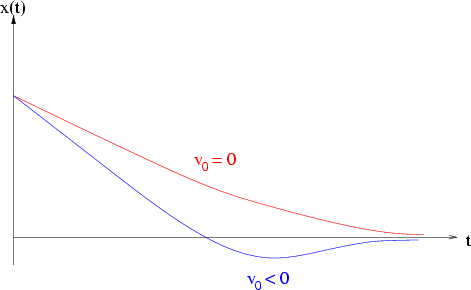
In diesem Fall ist die Lösung eine abfallende Exponentialfunktion: der Massenpunkt ''kriecht'' aus seiner
Anfangsauslenkung in unendlicher Zeit in die Gleichgewichtslage.
- (2)
- Aperiodischer Grenzfall:
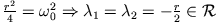
Abbildung 3.7:
Aperiodischer Grenzfall.
 |
In diesem Fall müssen wir ein Fundamentalsystem konstruieren, da
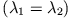 wir nur
eine Lösung erhalten.
wir nur
eine Lösung erhalten.
Beh.:
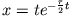 ist ebenfalls eine Lösung.
ist ebenfalls eine Lösung.
Einsetzen in die Differentialgleichung mit
zeigt, dass
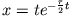 ebenfalls eine Lösung der Differentialgleichung ist.
Wir erhalten die allgemeine Lösung für den aperiodischen Grenzfall
und die physikalisch realisierte Lösung unter Berücksichtigung der Anfangsbedingungen
ebenfalls eine Lösung der Differentialgleichung ist.
Wir erhalten die allgemeine Lösung für den aperiodischen Grenzfall
und die physikalisch realisierte Lösung unter Berücksichtigung der Anfangsbedingungen
- (3)
- Oszillatorlösung:
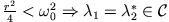 .
Für komplexwertige Exponenten erhalten wir für die allgemeine Lösung ein oszillatorisches Verhalten
Mit den Anfangsbedingungen ergibt sich dann
.
Für komplexwertige Exponenten erhalten wir für die allgemeine Lösung ein oszillatorisches Verhalten
Mit den Anfangsbedingungen ergibt sich dann
Abbildung 3.8:
Oszillatorlösung
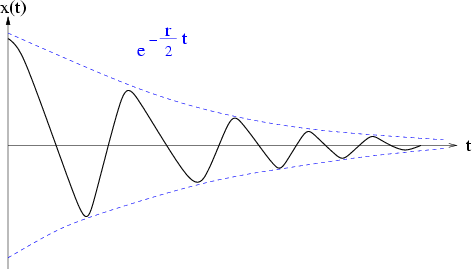 |
Bemerkungen:
- (i)
- Die Periode des gedämpften Oszillators
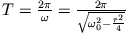 unterscheidet sich von der Periode des freien Oszillators
unterscheidet sich von der Periode des freien Oszillators
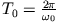 je stärker die Reibung ist.
Es gilt
je stärker die Reibung ist.
Es gilt 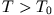 und für den Fall
und für den Fall
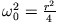 gilt
gilt
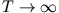 (aperiodischer Grenzfall).
(aperiodischer Grenzfall).
- (ii)
- Ein Maß für die Dämpfung ist die Abklingzeit
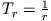 . Nach der Zeit
. Nach der Zeit 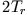 ist die
Amplitude auf
ist die
Amplitude auf
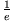 des Anfangswertes abgefallen.
des Anfangswertes abgefallen.
- (iii)
- Man definiert den Quotient aus den beiden Zeitkonstanten des Systems, nämlich
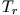 und
und 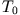 , als
Qualitätsfaktor oder Q-Wert des Oszillators,
, als
Qualitätsfaktor oder Q-Wert des Oszillators,
| Oszillator |
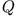 |
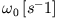 |
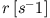 |
| Mechanisches Pendel |
 |
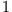 |
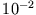 |
| Stimmgabel |
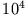 |
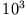 |
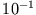 |
| FM Tuner |
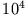 |
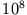 |
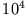 |
| angeregtes Atom |
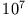 |
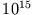 |
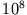 |
Im Falle des angeregten Atoms ist
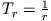 das Maß für die Lebensdauer des Zustandes
und
das Maß für die Lebensdauer des Zustandes
und
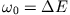 die Anregungsenergie.
die Anregungsenergie.
- (iv)
- Für die Energie des gedämpften Oszillators erhält man in Analogie zu Abschnitt 3.2 mit
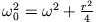
Ist die Reibung schwach, gilt
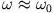 und
und 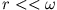 , so dass wir die Energie approximieren können
, so dass wir die Energie approximieren können
Wie zu erwarten nimmt die mechanische Gesamtenergie in einem dissipativen Oszillator mit der Zeit exponentiell ab.
Eine Periode später erhält man für die Gesamtenergie
Generell gilt für zwei benachbarte Perioden für den Energieverlust
bzw. für den prozentualen (relativen) Energieverlust
Die Periode des gedämpften Oszillators ist (binomische Entwicklung von
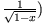 Bei schwacher Dämpfung
Bei schwacher Dämpfung
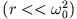 erhält man somit
erhält man somit
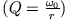 d.h. der inverse Q-Wert eines Oszillators ist ein Maß für den Energieverlust pro Periode.
d.h. der inverse Q-Wert eines Oszillators ist ein Maß für den Energieverlust pro Periode.
U. Lechner, H.J. Lüdde
![]() wir nur
eine Lösung erhalten.
wir nur
eine Lösung erhalten.
![]() ist ebenfalls eine Lösung.
ist ebenfalls eine Lösung.
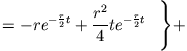
![]() und
und ![]() , so dass wir die Energie approximieren können
, so dass wir die Energie approximieren können