Im einfachsten Fall lautet die Bewegungsgleichung (3.1)
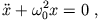 |
(3.2) |
d.h. ein harmonischer Oszillator ohne Reibung und äußeren Antrieb.
Als Ansatz für die Lösung betrachten wir
und setzen in die Bewegungsgleichung ein
Diese Gleichung muss für alle 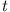 erfüllt werden, was nur möglich ist,
wenn
ist. Die Lösung dieser charakteristischen Gleichung ist rein
imaginär
und man erhält somit zwei linear unabhängige Lösungen
Diese beiden Lösungen nennt man das Fundamentalsystem der
Differentialgleichung (3.2). Wegen der Linearität der Bewegungsgleichung ist
jede beliebige Superposition der Fundamentallösung ebenfalls
eine Lösung der Differentialgleichung, also
erfüllt werden, was nur möglich ist,
wenn
ist. Die Lösung dieser charakteristischen Gleichung ist rein
imaginär
und man erhält somit zwei linear unabhängige Lösungen
Diese beiden Lösungen nennt man das Fundamentalsystem der
Differentialgleichung (3.2). Wegen der Linearität der Bewegungsgleichung ist
jede beliebige Superposition der Fundamentallösung ebenfalls
eine Lösung der Differentialgleichung, also
Dies ist die allgemeine Lösung der Differentialgleichung (3.2).
Sie stellt eine Lösungsschar dar als Funktion der Parameter 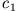 und
und 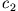 .
.
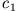 und
und 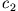 sind Integrationskonstanten, die wir im Prinzip durch die
zweifache formale Integration der Differentialgleichung (3.2) erhalten haben.
Um aus der Lösungsschar eine physikalische Lösung zu erhalten, müssen wir die
Anfangsbedingungen der Bewegung berücksichtigen
Einsetzen in die allgemeine Lösung ergibt
sind Integrationskonstanten, die wir im Prinzip durch die
zweifache formale Integration der Differentialgleichung (3.2) erhalten haben.
Um aus der Lösungsschar eine physikalische Lösung zu erhalten, müssen wir die
Anfangsbedingungen der Bewegung berücksichtigen
Einsetzen in die allgemeine Lösung ergibt
Daraus erhält man
Damit haben wir als physikalische Lösung des harmonischen Oszillators
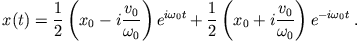 |
(3.3) |
Diesen Ausdruck können wir umformen, denn mit
gilt für (3.3)
Wir sehen also, dass die Lösung (3.3) reell ist und somit einen physikalisch beobachtbaren
Bewegungsablauf beschreibt. Die Lösung lässt sich aber noch in einer dritten Form angeben.
Ausgehend von der reellen Form erhält man mit Hilfe des Kosinussatzes
durch Koeffizientenvergleich
Bemerkungen:
- (i)
- Die verschiedenen Formen der Lösung (3.3) sind identische Beschreibungen der Bewegung
eines freien (ungedämpft und ohne äußeren Antrieb) harmonischen Oszillators: der Massenpunkt oszilliert mit konstanter Amplitude und Frequenz. Charakteristisch für die harmonische Bewegung ist, dass die Frequenz unabhängig von der Amplitude ist.
- (ii)
- Die letzte Form zeigt, wie sich die Lösungen abhängig von den Anfangsbedingungen unterscheiden
können: Amplitude A und Phase
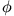 sind direkt von den Anfangsbedingungen abhängig,
sind direkt von den Anfangsbedingungen abhängig,
Abbildung 3.3:
Lösung des freien harmonischen Oszillators.
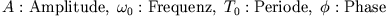
 |
Beispiel
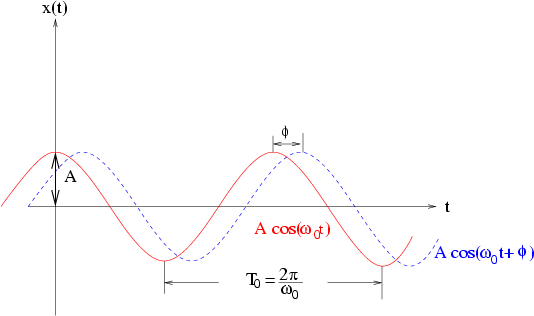
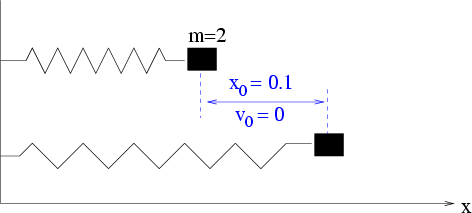
B3.1 Berechne die Bewegung des horizontalen Federpendels.
Die Masse 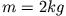 wird um
wird um 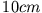 mit einer Kraft von
mit einer Kraft von
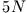 aus der entspannten Federposition ausgelenkt und dann losgelassen.
aus der entspannten Federposition ausgelenkt und dann losgelassen.
Abbildung 3.4:
Federpendel
 |
- Lösung:
- a)
- Berechne Federkonstante k:
- b)
- Berechne Frequenz
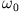 :
:
- c)
- Berechne A und
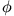 aus den Anfangsbedingungen:
aus den Anfangsbedingungen:
Das Weg-Zeit-Gesetz lautet somit
3.1.1 Energie des freien harmonischen Oszillators
Da die Rückstellkraft konservativ ist, ist die totale mechanische Energie
erhalten und es gilt (E:Gesamtenergie, T:kinetische Energie, U:potentielle Energie)
Durch Einsetzen der Lösung haben wir so im Retrospekt bewiesen, dass E eine Erhaltungsgröße ist.
Das wird im Oszillator dadurch erreicht, dass kinetische Energie und potentielle Energie gegenphasig oszillieren
U. Lechner, H.J. Lüdde
