3.6.2 Das getriebene mathematische Pendel - chaotische Bewegungsformen

Wir betrachten ein Pendel mit Stoke'schem Reibungsterm und einer äußeren periodischen Anregung des Typs der Abbildung (3.16a). In Abhängigkeit von der Kopplungsstärke der äußeren Anregung beobachtet man verschiedene Bewegungsformen: : gedämpfter Oszillator, : Einschwingvorgang und Grenzkreislösung des angeregten Oszillators, : nichtperiodischer Oszillator.

Abbildung 3.22: Getriebenes Pendel für (schwarz), 0.5 (blau) und 1.2 (grün).

Abbildung 3.23: Phasenraumtrajektorie des getriebenen Pendels.

Die letzte Bewegungsform unterscheidet sich deutlich von dem, was wir bisher unter einem Oszillator verstehen: innerhalb der 60s ist keine periodische Wiederholung der Schwingungsform erkennbar. Möglich wäre natürlich, dass der Einschwingvorgang für diesen Fall länger dauert, so dass man die Grenzkreislösung nach 60s noch nicht erreicht hat. Die folgende Abbildung zeigt eine Phasenraumdarstellung aufgenommen über 600s.

Abbildung 3.24: Phasenraumtrajektorie für für .

Offenbar unterscheidet sich diese Bewegungsform vollständig von den regulären Lösungen Rotator- oder Pendelbewegung. Sie erscheint vollkommen unvorhersehbar (chaotisch) und trotzdem werden wir im nächsten Abschnitt erste Schritte zu ihrer Analyse kennen lernen.

a)

Lyapunovexponent
Wir wollen die Bewegungsform für etwas genauer untersuchen. Dazu betrachten wir den Fall, was passiert, wenn wir die Anfangsbedingung minimal verstimmen. D.h. wir vergleichen zwei Lösungen zu Anfangsbedingungen, die sich nur um voneinander unterscheiden und beobachten die Differenz der Lösungen über die Zeit (Abb. 3.25).

Abbildung 3.25: Lyapunovexponent für reguläre und chaotische Bewegungsformen

Man sieht an der halblogarithmischen Darstellung, dass die Differenz der Lösungen für die Fälle im Mittel exponentiell abfällt, während sie für den Fall exponentiell zunimmt. Während im Fall der regulären Bewegungsformen alle Lösungen unabhängig von den Anfangsbedingungen gegen eine stabile asymptotische Lösung konvergieren (stabile Punktlösung für , stabiler Grenzkreis für ), ist dies für die irreguläre Lösung nicht der Fall: die Lösungen zu minimal unterschiedlichen Anfangsbedingungen streben exponentiell auseinander. Die Steigung der mittleren Differenz in der halblogarithmischen Darstellung nennt man Lyapunovexponent. Ist der Lyapunovexponent positiv, so verhält sich eine Lösung chaotisch.

b)

Poincare Schnitte
Ein weiteres nützliches Hilfsmittel zur Analyse chaotischer Systeme sind Poincare Schnitte. In diesem Fall zeichnet man z.B. nur solche Punkte des Phasenraumes, die in Phase mit der äußeren Anregung sind. Diese Bedingung wirkt in Analogie zu einem Stroboskop: Betrachtet man eine schnell rotierende Scheibe mit einer Aufschrift, so lässt sich der Text nicht lesen. Beleuchtet man jedoch die Scheibe mit einem Stroboskop in Phase (also z.B. immer, wenn die Schrift aufrecht steht), so erscheint der Text in Ruhe und man kann ihn gut erkennen. Übertragen auf das getriebene mathematische Pendel sammeln wir alle erreichbaren Phasenraumpunkte zu den Zeiten (Aufblitzen der Stroboskoplampe) . Für eine reguläre Bewegung würde man nach einem kurzen Einschwingverhalten genau einen Punkt sehen, da die Bewegungsformen asymptotisch durch einen Attraktor (Fokus bzw. Grenzzyklus) bestimmt sind.

Abbildung 3.26: Seltsamer Attraktor des mathematischen Pendels

Im Fall der chaotischen Lösung könnte man erwarten, dass der erreichbare Phasenraum lückenlos erfüllt wird: man findet aber eine regelmäßige Struktur. Das Pendel kehrt immer wieder in bestimmte Regionen des Phasenraumes zurück. Vergrößert man diese Regionen sieht man, dass sie sich immer nur aus isolierten Phasenpunkten zusammensetzen: man sagt die Dimension des Attraktors (also jenes Gebiet des Phasenraumes, zu dem die Lösung immer wiederkehrt) ist fraktal (gebrochen). Es handelt sich also weder um eine Raumkurve (Dimension 1), noch um eine Raumfläche (Dimension 2). Solche Attraktoren mit fraktaler Dimension nennt man seltsame Attraktoren. Sie sind charakteristisch für chaotische Systeme.

c)

Periodenverdopplung - ein Weg zum Chaos
Bisher haben wir zwei typische Eigenschaften chaotischer Bewegungsformen diskutiert: (i)die extreme Abhängigkeit einer chaotischen Lösung von ihrer Anfangsbedingung und (ii) die charakteristische topologische Struktur ihres seltsamen Attraktors. In diesem Abschnitt wollen wir der Frage nachgehen, inwieweit sich der Übergang zwischen einer regulären und einer chaotischen Bewegungsform durch Variation der äußeren Kraft 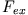ankündigt. Dazu betrachten wir in der folgenden Abbildung drei reguläre Lösungen des getriebenen Pendels für die Kopplungsstärken .

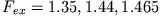Abbildung 3.27: Periodenverdopplungen regulärer Lösungen für a) 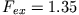, b) und c)

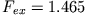
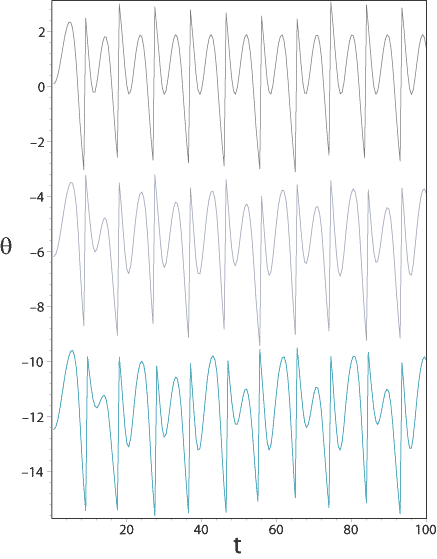Nach einem Einschwingvorgang 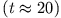findet man eine reguläre Grenzkreislösung mit Periode 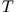für 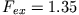. Ändert man den Wert für 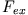, stellt man fest, dass sich die Periode der Grenzkreislösung bei einem bestimmten Wert spontan verdoppelt (für erkennt man verschieden hohe Maxima, bevor sich die Lösung periodisch wiederholt). Eine kleine Vergrößerung von 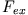bewirkt eine weitere spontane Verdopplung der Periode, bis man im Grenzfall unendlich vieler Periodenverdopplungen eine irreguläre (chaotische) Lösung erhält.
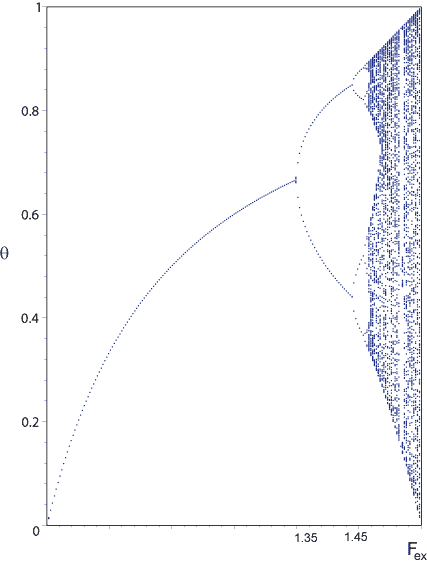
Trägt man die auf das Intervall [0,1] normierten Maxima von 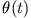als Funktion von 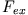auf, so erhält man ein Bifurkationsdiagramm (Bifurkation: Gabelung), das in immer kürzeren Abständen des Kontrollparameters 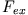Verzweigungspunkte aufweist, bis im Grenzfall unendlicher Verzweigung die Maxima beliebig dicht liegen, die Bewegung schließlich chaotisch wird.

Abbildung 3.28: Feigenbaumdiagramm (Bifurkationsdiagramm)

Dabei genügt die Folge der Bifurkationspunkte 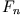einer universellen Regel: Definiert man das Abstandsmaß

so findet man als Grenzwert den universellen Feigenbaumparameter

Für alle Systeme, deren reguläre Lösungen durch Periodenverdopplung in chaotische Lösungen übergehen, erhalten wir den Feigenbaumparameter als Grenzwert der Folge 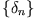. Wir haben somit ein eindeutiges Maß dafür, wie ''nahe'' wir uns an einer chaotischen Lösung befinden. Dieses Maß 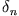könnte man z.B. als ''Regler'' benutzen, um den Parameter 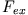so zu kontrollieren, dass die Lösungen z.B. immer regulär bleiben.

Alle Überlegungen dieses Abschnitts lassen sich mit Hilfe des Arbeitsblattes Das mathematische Pendel interaktiv nachvollziehen.