Oszillatoren haben in allen Bereichen der Physik deshalb eine so
große Bedeutung, weil die Potentialfunktionen energieerhaltender
Systeme in der Nachbarschaft von Gleichgewichtslösungen durch ein
Oszillatorpotential approximiert werden können.
In erster Näherung ist das Oszillatorpotential quadratisch
und damit die Kraft linear. Diese spezielle Form eines Oszillators
mit linearem Kraftgesetz nennt man ''harmonischen Oszillator''.
Wir werden sehen, dass für harmonische Oszillatoren kennzeichnend ist,
dass die Frequenz unabhängig von der Amplitude ist.
Charakteristisch für die Oszillatorbewegung ist, dass die Kraft
auf den Massenpunkt immer auf den Ort der Gleichgewichtslösung
hingerichtet ist: aus diesem Grund nennt man die Kraft
''die Rückstellkraft''. Neben der Rückstellkraft wird der
Oszillator durch Reibungskräfte und möglicherweise durch
eine zeitabhängige äußere treibende Kraft beeinflusst,
In der Mechanik wird der harmonische Oszillator realisiert durch
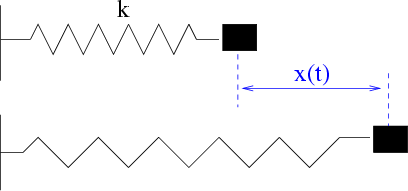
z.B. das horizontale Federpendel (Abb. 3.1)
Abbildung 3.1:
Horizontales Federpendel
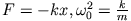
 |
oder das mathematische Pendel (Abb. 3.2),
Abbildung 3.2:
Mathematisches Pendel. Bei kleinen Ausschlägen gilt
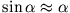 und für das Bogenelement
und für das Bogenelement
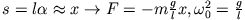
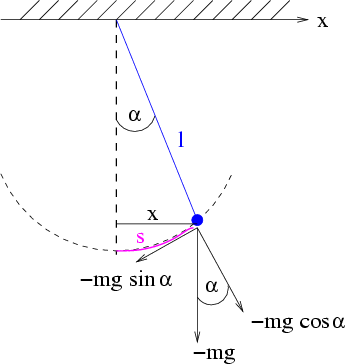 |
beide in ihrer jeweils linearisierten Form.
Für das Federpendel findet man
wobei k (die Federkonstante) ein Maß für die Stärke der Feder darstellt.
Für das mathematische Pendel ist die Rückstellkraft
zunächst nichtlinear.
Bei kleinen Ausschlägen gilt aber
und somit
Die Reibungskraft ist proportional zur Geschwindigkeit und der Bewegung
entgegengerichtet, also (Reibungskoeffizient 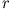 )
Die antreibende Kraft ist nur zeitabhängig und überträgt mechanische Energie
auf das Pendel.
Als Bewegungsgleichung ergibt sich somit generisch für alle harmonischen Oszillatoren
)
Die antreibende Kraft ist nur zeitabhängig und überträgt mechanische Energie
auf das Pendel.
Als Bewegungsgleichung ergibt sich somit generisch für alle harmonischen Oszillatoren
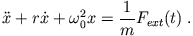 |
(3.1) |
Entscheidend ist die lineare Rückstellkraft. Mathematisch handelt es sich bei (3.1) um eine
gewöhnliche, lineare Differentialgleichung 2. Ordnung mit
konstanten Koeffizienten.
Man nennt sie homogen für 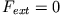 , sonst inhomogen.
Diese Begriffe sind wichtig für die weitere Diskussion.
, sonst inhomogen.
Diese Begriffe sind wichtig für die weitere Diskussion.
U. Lechner, H.J. Lüdde