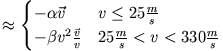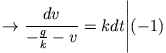2.3 Geschwindigkeitsabhängige Kräfte

Wenn wir uns durch ein Medium bewegen (Luft oder Wasser), so spüren wir abhängig von unserer Geschwindigkeit eine Widerstandskraft, deren Ursache damit verbunden ist, dass wir mit unserem Körper das Medium verdrängen müssen. Aus Erfahrung wissen wir, dass diese Reibungskraft mit wachsender Geschwindigkeit zunimmt (Beispiele: Luftwiderstand beim Fahrrad- oder Motorradfahren; Wasserverdrängung beim Turmspringen aus unterschiedlichen Höhen). Etwas genauer findet man experimentell (Windkanalversuche) für die Reibungskraft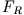

Die Reibungskraft ist also immer der Bewegung entgegen gerichtet. Sie ist proportional zu 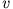bei kleinen Geschwindigkeiten (Reibung nach Stokes) und abhängig von 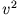bei großen Geschwindigkeiten (Reibung nach Newton). Für Geschwindigkeiten nahe der Schallgeschwindigkeit gelten eigene Gesetzmäßigkeiten. In die Koeffizienten 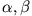gehen vor allem die Querschnittsfläche des Körpers und seine Oberflächenbeschaffenheit ein. Systeme mit Reibungskräften sind nicht konservativ, da sie nicht die mechanische Gesamtenergie erhalten (Beispiel: beim Eintritt eines Körpers in die Erdatmosphäre wird Reibungshitze erzeugt, die der mechanischen Energie entzogen wird). Im Gegensatz zu konservativen Systemen nennt man geschwindigkeitsabhängige Kräfte dissipativ.

B2.7 Gebremster Fall mit Luftreibung

Die Bewegungsgleichung lautet

Im Gegensatz zum freien Fall ohne Reibung ist die wirkende Kraft nicht mehr konstant, so dass wir die Bewegungsgleichung nicht mehr direkt integrieren können. Zur allgemeinen Lösung benutzen wir die Methode der Separation der Variablen und erhalten

(Überprüfen durch Ausmultiplizieren!) Da 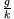konstant und somit 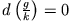ist, erhalten wir

Integration beider Seiten ergibt mit der Integrationskonstante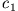

bzw. mit

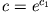
Berücksichtigt man als Anfangsbedingung 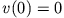, so können wir 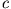bestimmen und erhalten schließlich

Für den Grenzfall kleiner Zeiten können wir die e-Funktion entwickeln (Taylorreihe)

D.h. zu Beginn ist der Fall ungebremst und entspricht dem freien Fall 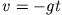. Im weiteren Verlauf setzt die Reibung merkbar ein. Nach einer langen Fallzeit erhält man

eine konstante Endgeschwindigkeit, abhängig von der Masse des fallenden Körpers und seinen Reibungseigenschaften.
Beachte:der freie Fall im Vakuum ist unabhängig von der Masse, der gebremste Fall im Medium nicht! Zur weiteren Veranschaulichung betrachten wir den Fall eines Fallschirmspringers mit Hilfe von Maple.