2.2.1 Potentiale

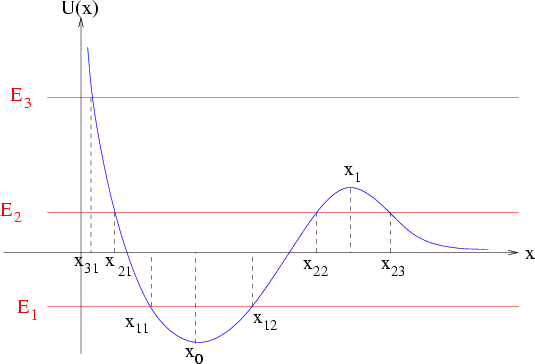
Abbildung 2.7: Analyse der Bewegungsform aus der Potentialfunktion

Kräfte heißen konservativ, wenn sie über ein Potential definiert sind, d.h.

Die mechanische Gesamtenergie setzt sich in diesem Fall zusammen aus kinetischer Energie 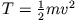und potentieller Energie 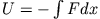. Kennt man die Potentialfunktion eines mechanischen Systems, so kann man bei gegebener Gesamtenergie

qualitative Aussagen über die mögliche Bewegungsform erhalten, ohne die Bewegungsgleichung lösen zu müssen. Man nennt einen Massenpunkt frei, wenn er sich beliebig im Raum bewegen kann und gebunden, wenn er im Raum lokalisiert ist. Ist z.B. 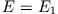(Abb. 2.7), so ist der Massenpunkt im Gebiet 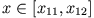gebunden. Er kann dieses Gebiet nicht verlassen, da für alle Punkte außerhalb des Intervalls 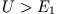ist und somit

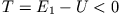
   für

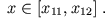
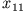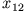Solche Orte, für die gilt, nennt man klassisch verbotene Raumbereiche. An den Randpunkten und ist 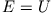, somit 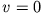, d.h. der Massenpunkt ist momentan bewegungslos und kann sich nur in umgekehrter Richtung weiterbewegen. Deshalb nennt man die Randpunkte Umkehrpunkte der Bewegung. Besitzt ein Massenpunkt die Energie 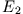, so ist er entweder im Intervall 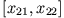gebunden oder für 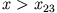frei. Ein Massenpunkt mit der Energie 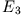kann sich frei im Raum bewegen außer im klassisch verbotenen Bereich 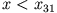. Berechnet man für die Potentialfunktion der Abb. 2.7 die Kraft 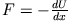, so sieht man, dass für 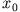und 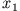die Kraft verschwindet. Solche Punkte nennt man Gleichgewichtspunkte oder stationäre Punktlösungen, für die gilt

(i)

Ein Massenpunkt mit Anfangsgeschwindigkeit 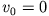befindet sich in den Punkten 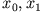, für die gilt

in Ruhe.

(ii)

Gilt mit

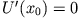
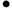
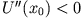. , so befindet sich der Massenpunkt in einem instabilen Gleichgewicht. Kleine Ortsveränderungen bewirken die unwiderrufliche Entfernung des Massenpunktes vom Ort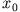

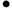
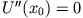. , so befindet sich der Massenpunkt in einem unbestimmten Gleichgewicht.

. , so befindet sich der Massenpunkt in einem stabilen Gleichgewicht. Kleine Ortsveränderungen bewirken stets eine Rückkehr zu .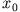

Das Arbeitsblatt Gleichgewicht: Kraft und potentielle Energie zeigt für eine gegebene Potentialfunktion die Zusammenhänge zwischen Kraft und potentieller Energie.